так що (5) рівносильне (2). Нарешті, мабуть, що (2) рівносильне
(1).
Визначення 12Знакозмінний простір  називається регулярним, якщо воно задовольняє
одному з п'яти рівносильних умов . Знакозмінний простір
називається регулярним, якщо воно задовольняє
одному з п'яти рівносильних умов . Знакозмінний простір  називається виродженим,
якщо воно не є регулярним. Нарешті, воно називається цілком виродженим, якщо
називається виродженим,
якщо воно не є регулярним. Нарешті, воно називається цілком виродженим, якщо 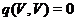 .
.
Якщо 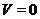 , то
, то  регулярно. Якщо
регулярно. Якщо 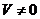 , то через і
, то через і
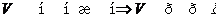
Пропозиція.13 Нехай 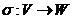 - уявлення знакозмінних просторів. Якщо
- уявлення знакозмінних просторів. Якщо  регулярно, то
регулярно, то  - ізометрія.
- ізометрія.
Доказ. Візьмемо 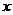 з ядра уявлення
з ядра уявлення  . Тоді
. Тоді 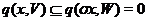 . Звідси через регулярність простору
. Звідси через регулярність простору  одержуємо, що
одержуємо, що 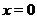 .
.
Пропозиція 14Кожній базі 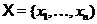 регулярного знакозмінного простору
регулярного знакозмінного простору  відповідає єдина база
відповідає єдина база
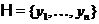 цього простору,
називана сполученої до
цього простору,
називана сполученої до 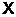 відносно
відносно 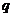 й така, що
й така, що 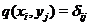 для всіх
для всіх 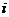 ,
, 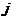 . Якщо
. Якщо 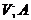 в
в 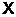 и
и 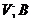 в
в 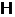 , то
, то  .
.
Доказ.1) Покладемо 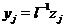 для
для 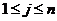 , де
, де 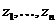 - сполучена до
- сполучена до 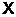 база сполученого простору
база сполученого простору 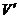 . Тоді
. Тоді 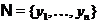 - база, тому що
- база, тому що 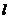 біективно. Крім того,
біективно. Крім того, 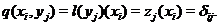 . Цим доведене існування бази
. Цим доведене існування бази
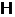 . Одиничність безпосередньо
треба з регулярності. 2) Нехай
. Одиничність безпосередньо
треба з регулярності. 2) Нехай 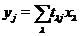 . Тоді
. Тоді 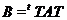 й
й 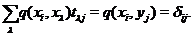 Звідси
Звідси
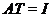 , так що
, так що 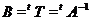 й
й  .
.
Розглянемо знакозмінний простір  зі знакозмінною формою
зі знакозмінною формою 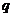 . Будемо говорити, що
. Будемо говорити, що
 має ортогональне
розкладання
має ортогональне
розкладання 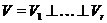 на підпростори
на підпростори 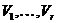 якщо воно є прямою сумою
якщо воно є прямою сумою 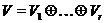 з попарно ортогональними
з попарно ортогональними 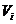 , тобто
, тобто 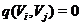 при
при 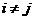 . Назвемо
. Назвемо 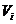 компонентами цього ортогонального
розкладання. Будемо говорити, що підпростір
компонентами цього ортогонального
розкладання. Будемо говорити, що підпростір  розщеплює
розщеплює  або що
або що  є компонентом простору
є компонентом простору  , якщо існує підпростір
, якщо існує підпростір 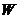 простору
простору  , таке, що
, таке, що 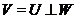 . Маємо
. Маємо 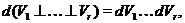 де добуток
береться в.
де добуток
береться в.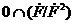
Важливим є випадок, коли 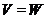 ,
, 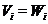 для всіх
для всіх 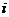 і
і 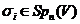 для всіх
для всіх 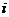 ; тоді
; тоді 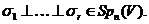
Якщо дано ще одне таке уявлення 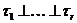 , то
, то
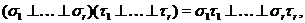
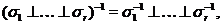
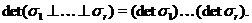
Розглянемо знакозмінний простір  над полем
над полем 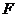 . Під ортогональним доповненням
підпростору
. Під ортогональним доповненням
підпростору  простору
простору
 в
в  розуміється підпростір
розуміється підпростір
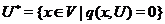
співпадаюче також з
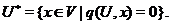
Визначимо радикал простору  як підпростір
як підпростір 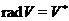 . Очевидно,
. Очевидно,
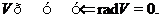
Пропозиція15 Нехай  - знакозмінний простір, що є сумою попарно ортогональних
підпросторів, тобто
- знакозмінний простір, що є сумою попарно ортогональних
підпросторів, тобто 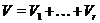 , де
, де 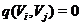 при
при 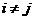 . Тоді
. Тоді
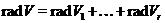 ,
,
 регулярно
регулярно 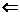 кожне
кожне 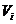 регулярно,
регулярно,
 регулярно
регулярно 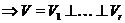 .
.
Доказ. (1) Візьмемо в 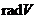 довільний елемент
довільний елемент 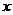 і запишемо його у вигляді
і запишемо його у вигляді 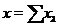 ,
, 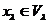 . Тоді
. Тоді
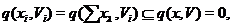
так що 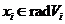 , звідки
, звідки 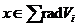 . Обернено, якщо
. Обернено, якщо 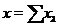 , де
, де 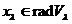 , те
, те 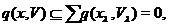 звідки
звідки  . (2)
Це треба з (1) і того, що знакозмінний простір регулярний тоді й тільки тоді, коли
його радикал дорівнює
. (2)
Це треба з (1) і того, що знакозмінний простір регулярний тоді й тільки тоді, коли
його радикал дорівнює 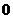 . (3)
Якщо
. (3)
Якщо 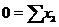 ,
, 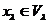 , те
, те 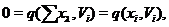 звідки
звідки
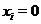 . Отже,
. Отже, 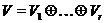 і, виходить,
і, виходить, 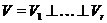 .
.
Пропозиція 16 Якщо  - підпростір знакозмінного простору
- підпростір знакозмінного простору  , те
, те 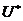 - анулятор простору
- анулятор простору 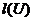 в
в  , тобто
, тобто 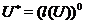 . Зокрема,
. Зокрема, 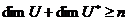 .
.
Доказ безпосередньо треба з визначень.
Пропозиція 17 Нехай  - регулярний підпростір знакозмінного простору
- регулярний підпростір знакозмінного простору
 . Тоді
. Тоді  розщеплює
розщеплює  , точніше,
, точніше, 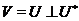 . Якщо
. Якщо 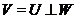 - інше розщеплення,
- інше розщеплення,
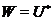 .
.
Доказ. Тому що  регулярно, те
регулярно, те 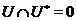 . Отже, через
. Отже, через

Тому 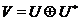 й, виходить,
й, виходить, 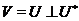 . Далі, якщо
. Далі, якщо 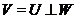 , те
, те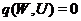 , звідки
, звідки 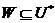 . Порівнюючи розмірності, одержуємо
. Порівнюючи розмірності, одержуємо 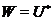 .
.
Пропозиція 18 Якщо  й
й 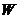 - довільні підпростори регулярного знакозмінного
простору
- довільні підпростори регулярного знакозмінного
простору  розмірності
розмірності
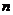 , те
, те
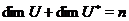 ,
,
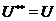 ,
,
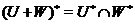 ,
,
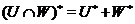 ,
,
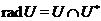 .
.
Доказ. Тому що  регулярно, те через відображення
регулярно, те через відображення 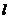 біективно. Отже,
біективно. Отже, 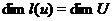 , звідки через
, звідки через 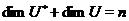 . Цим
доведено (1). Далі,
. Цим
доведено (1). Далі, 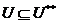 , тому порівняння дає
, тому порівняння дає 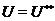 . Цим доведено (2). Доведемо тепер (3):
. Цим доведено (2). Доведемо тепер (3):
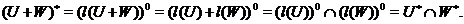
Аналогічно доводиться (4). Нарешті, твердження (5) тривіально.
Розглянемо радикал 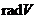 знакозмінного простору
знакозмінного простору  , і нехай
, і нехай  - підпростір простору
- підпростір простору  , таке, що
, таке, що 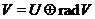 . Назвемо всяке таке розкладання
радикальним розкладанням простору
. Назвемо всяке таке розкладання
радикальним розкладанням простору  . Очевидно,
. Очевидно,  визначається не єдиним образом, за винятком випадків,
коли
визначається не єдиним образом, за винятком випадків,
коли  регулярно
або цілком вироджене.
регулярно
або цілком вироджене.
Зі співвідношень

треба рівність 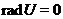 , тому
, тому  регулярно.
регулярно.
Теорема 19 Якщо  - регулярний знакозмінний простір розмірності
- регулярний знакозмінний простір розмірності 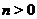 , те
, те
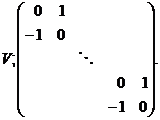
Зокрема, регулярний знакозмінний простір має парну розмірність
і дискримінант 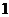 .
Крім того, регулярні знакозмінні простори однакової розмірності над тим самим полем
.
Крім того, регулярні знакозмінні простори однакової розмірності над тим самим полем
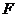 ізометричні.
ізометричні.
Доказ. Через регулярність простору  існують вектори
існують вектори 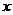 й
й 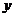 , що задовольняють умові
, що задовольняють умові 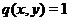 . Тому що
. Тому що 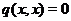 , те ці вектори повинні
бути незалежними; тому
, те ці вектори повинні
бути незалежними; тому 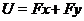 - площина. Очевидно,
- площина. Очевидно,
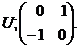
Зокрема,  регулярно, тому що дискримінант відмінний від нуля.
Отже, через
регулярно, тому що дискримінант відмінний від нуля.
Отже, через 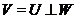 . Але
. Але 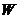 - також регулярний знакозмінний простір. Перше
твердження треба тепер з міркувань індукції. Друге тривіально треба з першого. Для
доказу третього твердження застосовуємо . Теорема доведена.
- також регулярний знакозмінний простір. Перше
твердження треба тепер з міркувань індукції. Друге тривіально треба з першого. Для
доказу третього твердження застосовуємо . Теорема доведена.
База 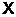 регулярного знакозмінного простору
регулярного знакозмінного простору  називається гіперболічної,
якщо
називається гіперболічної,
якщо
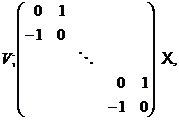
і сімплектичною, якщо
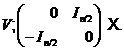
Якщо
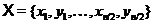
гіперболічна база простору  , то перестановка
, то перестановка
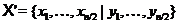
симплектична база, і навпаки. По теоремі ненульовий регулярний знакозмінний простір має гіперболічну базу, а тому
й симплектичну базу.
Пропозиція 20 Нехай  - регулярний знакозмінний простір,
- регулярний знакозмінний простір, 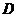 - цілком вироджений
підпростір і
- цілком вироджений
підпростір і 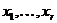 -
база підпростору
-
база підпростору 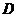 . Тоді існує регулярний підпростір
. Тоді існує регулярний підпростір  простору
простору  виду
виду 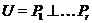 , де
, де 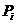 - регулярні площини й
- регулярні площини й 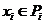 ,
, 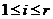 .
.
Доказ. Випадок 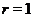 очевидний. При
очевидний. При 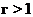 застосовуємо індукцію по
застосовуємо індукцію по 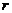 . Покладемо
. Покладемо 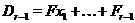 й
й 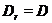 . Тоді
. Тоді 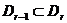 , звідки
, звідки 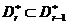 через . Виберемо
через . Виберемо 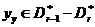 й покладемо
й покладемо 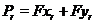 . Тоді
. Тоді 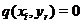 ,
, 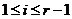 , і, отже,
, і, отже, 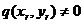 . Виходить,
. Виходить, 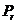 - регулярна площина, що містить
- регулярна площина, що містить 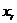 . У силу можна записати
. У силу можна записати 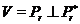 . Тоді
. Тоді 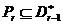 , тому що
, тому що 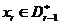 й
й 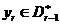 отже,
отже, 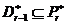 . Залишається застосувати припущення індукції до
. Залишається застосувати припущення індукції до
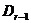 розглянутого як
підпростір знакозмінного простору
розглянутого як
підпростір знакозмінного простору 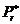 .
.
Пропозиція 21 Якщо 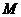 - максимальне цілком вироджений підпростір регулярного
знакозмінного простору
- максимальне цілком вироджений підпростір регулярного
знакозмінного простору  , те
, те 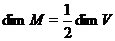 . Доказ.
Тому що
. Доказ.
Тому що 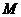 цілком
вироджене, те
цілком
вироджене, те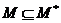 ,
тому через
,
тому через 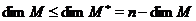 , звідки
, звідки 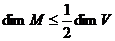 .
.
Якщо допустити, що 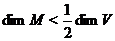 , то нескладне застосування тверджень і дасть цілком вироджений підпростір, що строго містить
, то нескладне застосування тверджень і дасть цілком вироджений підпростір, що строго містить
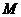 у протиріччя з
максимальністю
у протиріччя з
максимальністю 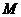 .
Тому
.
Тому 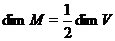 .
.
Пропозиція.22 Якщо 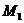 й
й 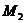 - максимальні цілком вироджені підпростору регулярного
знакозмінного простору
- максимальні цілком вироджені підпростору регулярного
знакозмінного простору  , що задовольняють умові
, що задовольняють умові 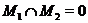 , то для кожної бази
, то для кожної бази 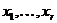 простору М існує така
база
простору М існує така
база 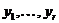 простору
простору
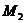 , що
, що 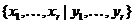 - симплектична база
простору
- симплектична база
простору  .
.
Доказ. Зрозуміло, 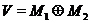 (через ). Нехай
(через ). Нехай 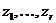 , - база підпростору
, - база підпростору 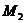 . Тоді
. Тоді 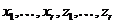 - база простору
- база простору  .
.
Нехай 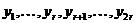 - сполучена до неї база відносно
- сполучена до неї база відносно 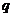 (див. ). Оскільки
(див. ). Оскільки 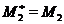 , те елементи
, те елементи 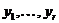 лежать в.
лежать в. 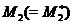 Виходить,
Виходить, 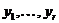 - база простору
- база простору 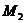 , а
, а 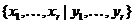 симплектична база в.
симплектична база в.
Пропозиція 23 Нехай  - регулярний знакозмінний простір і
- регулярний знакозмінний простір і 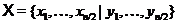 його
симплектична база.
його
симплектична база.
Нехай 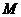 - максимальне цілком вироджений простір
- максимальне цілком вироджений простір 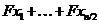 . Тоді матричний ізоморфізм,
асоційований з
. Тоді матричний ізоморфізм,
асоційований з 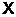 ,
відображає групу лінійних перетворень
,
відображає групу лінійних перетворень 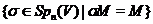 на групу матриць виду
на групу матриць виду
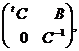
де 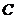 - оборотна
- оборотна 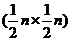 - матриця, а
- матриця, а 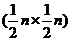 - матриця
- матриця 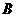 задовольняє співвідношенню
задовольняє співвідношенню 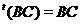 .
.
Доказ. Це легко перевіряється належним застосуванням твердження
.
Теорема Витта 24 Нехай  і
і 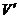 - ізометричні регулярні знакозмінні простори над
тим самим полем
- ізометричні регулярні знакозмінні простори над
тим самим полем 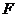 .
Якщо
.
Якщо  - довільний
підпростір простору
- довільний
підпростір простору  й
й  - ізометрія
- ізометрія  в
в 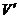 , то її можна продовжити до ізометрії простору
, то її можна продовжити до ізометрії простору  на
на 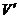 .
.
Доказ. Візьмемо радикальне розкладання 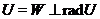 , і нехай
, і нехай 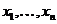 - база підпростору
- база підпростору 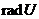 (мається на увазі,
що
(мається на увазі,
що 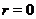 , якщо
, якщо 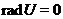 ). Застосовуючи до регулярного знакозмінного простору
). Застосовуючи до регулярного знакозмінного простору 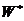 , ми бачимо, що в ньому існує підпростір
, ми бачимо, що в ньому існує підпростір 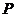 виду
виду 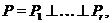 е
е 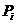 - регулярні площини
й
- регулярні площини
й 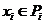 ,
, 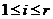 . Тому що
. Тому що 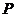 регулярно, те воно
розщеплює
регулярно, те воно
розщеплює 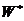 ; отже,
існує регулярний підпростір
; отже,
існує регулярний підпростір 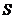 простору
простору 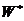 , таке, що
, таке, що 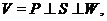
Покладемо 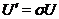 ,
, 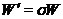 і
і 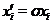 для
для 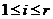 . Тоді
. Тоді 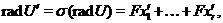 Крім того,
Крім того, 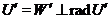 радикальне
розкладання. Ми можемо повторити попередні міркування й одержати розкладання
радикальне
розкладання. Ми можемо повторити попередні міркування й одержати розкладання 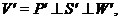 у якому
у якому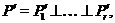 де
де 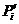 - регулярна площина й
- регулярна площина й 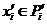 для
для 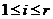 . За допомогою знайдемо ізометрію простору
. За допомогою знайдемо ізометрію простору 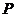 на
на 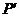 , погоджену з
, погоджену з  на кожному
на кожному 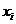 , а отже, на
, а отже, на 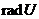 . Крім того, дане
. Крім того, дане  відображає
відображає 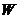 на
на 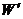 . Виходить, існує продовження ізометрії
. Виходить, існує продовження ізометрії  до ізометрії простору
до ізометрії простору
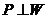 на
на 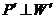 .
.
Далі 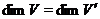 , тому що
, тому що  ізометричне
ізометричне 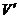 , тому
, тому 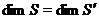 й, отже, по теоремі існує ізометрія простору
й, отже, по теоремі існує ізометрія простору 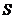 на
на 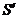 . Таким чином, існує продовження ізометрії
. Таким чином, існує продовження ізометрії  до ізометрії простору
до ізометрії простору
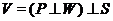 на
на 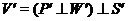 .
.
5. Проективні перетворення
Геометричне перетворення 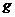 абстрактного векторного простору
абстрактного векторного простору  на абстрактний векторний
простір
на абстрактний векторний
простір 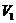 - це біекція
- це біекція
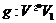 з наступною властивістю:
підмножина
з наступною властивістю:
підмножина 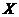 простору
простору
 тоді й тільки
тоді є підпростором в
тоді й тільки
тоді є підпростором в  , коли
, коли 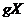 - підпростір в.
- підпростір в.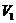
Очевидно, що композиція геометричних перетворень - геометричне
перетворення й перетворення, зворотне до геометричного, - також геометричне. Геометричне
перетворення зберігає включення, об'єднання й перетинання підпросторів, а також
ряди Жордана - і Гельдера, що тому справедливо випливає пропозиція.
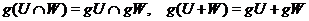
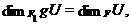
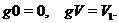
Під проективним простором 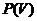 простору
простору  ми будемо розуміти множину всіх підпросторів
простору
ми будемо розуміти множину всіх підпросторів
простору  . Таким
чином,
. Таким
чином, 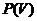 складається
з елементів множини
складається
з елементів множини 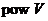 , що є підпросторами в
, що є підпросторами в  ;
; 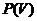 . Будь-які два елементи
. Будь-які два елементи  й
й 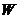 з
з 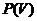 мають об'єднання й перетинання, а саме
мають об'єднання й перетинання, а саме 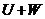 й
й 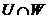 , так що
, так що 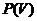 - ґрати; вона має найбільший
елемент
- ґрати; вона має найбільший
елемент  і найменший
елемент
і найменший
елемент 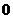 . Кожному
елементу
. Кожному
елементу  простору
простору
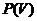 зіставляється
число
зіставляється
число 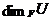 . Кожне
. Кожне  з
з 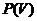 володіє поруч Жордана - Гельдера
володіє поруч Жордана - Гельдера
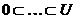 , і всі такі ряди
мають довжину
, і всі такі ряди
мають довжину 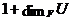 .
Покладемо
.
Покладемо
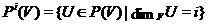
і назвемо 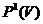 ,
, 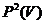 ,
, 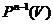 множинами прямих, площин і гіперплощин простору
множинами прямих, площин і гіперплощин простору
 відповідно.
відповідно.
Проективність 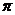 простору
простору  на
на 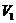 - це біекция
- це біекция 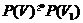 з наступною властивістю: для будь-яких
з наступною властивістю: для будь-яких  ,
, 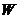 із
із 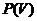 включення
включення 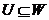 має місце тоді й тільки тоді, коли
має місце тоді й тільки тоді, коли 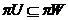 .
.
Очевидно, що композиція проективностей - проективність
і відображення, зворотне до проективності, - також проективність. Проективність
простору  на
на 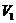 зберігає порядок, об'єднання,
перетинання й ряди Жордана - Гельдера для елементів просторів
зберігає порядок, об'єднання,
перетинання й ряди Жордана - Гельдера для елементів просторів 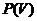 і
і 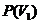 , що тому справедливо випливає пропозиція.
, що тому справедливо випливає пропозиція.
Пропозиція 26 Якщо 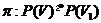 - проективність простору
- проективність простору  на
на 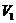 , те для будь-яких елементів
, те для будь-яких елементів  ,
, 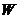 з
з 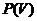 виконуються співвідношення
виконуються співвідношення
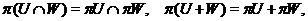
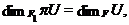
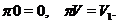
Зокрема, 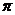 відображає
відображає 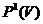 на
на 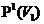 й визначається своїми значеннями на
й визначається своїми значеннями на 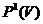 , тобто на прямих.
, тобто на прямих.
Якщо 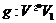 - геометричне перетворення, то відображення
- геометричне перетворення, то відображення 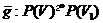 , отримане зі
, отримане зі 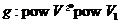 звуженням, є проективністю
простору
звуженням, є проективністю
простору  на
на 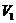 . Усяка проективність
. Усяка проективність
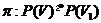 , що має вид
, що має вид 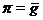 для деякого такого
для деякого такого
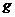 , буде називатися
проективним геометричним перетворенням простору
, буде називатися
проективним геометричним перетворенням простору  на
на 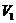 . Чортові ми будемо завжди використовувати для позначення
проективного геометричного перетворення
. Чортові ми будемо завжди використовувати для позначення
проективного геометричного перетворення 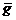 , отриманого описаним способом з геометричного перетворення
, отриманого описаним способом з геометричного перетворення
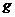 . Таким чином,
. Таким чином,
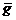 переводить підпростір
переводить підпростір
 простору
простору  , тобто крапку
, тобто крапку  з
з 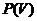 , у підпростір
, у підпростір 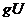 простору
простору 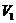 . Маємо
. Маємо
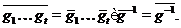
Зокрема, композиція проективних геометричних перетворень
і перетворення, зворотне до проективного геометричного, самі є проективними геометричними.
Геометричне перетворення простору  є по визначенню геометричне
перетворення простору
є по визначенню геометричне
перетворення простору  на себе. Множина геометричних перетворень простору
на себе. Множина геометричних перетворень простору
 є підгрупою групи
підстановок множини
є підгрупою групи
підстановок множини  . Вона буде позначатися через
. Вона буде позначатися через 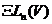 і називатися загальною геометричною
групою простору
і називатися загальною геометричною
групою простору  .
Під групою геометричних перетворень простору
.
Під групою геометричних перетворень простору  ми будемо розуміти довільну підгрупу групи
ми будемо розуміти довільну підгрупу групи 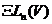 . Загальна лінійна група
. Загальна лінійна група
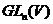 й спеціальна лінійна
група
й спеціальна лінійна
група 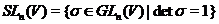 є, отже,
групами геометричних перетворень. Під групою лінійних перетворень будемо розуміти
будь-яку підгрупу групи
є, отже,
групами геометричних перетворень. Під групою лінійних перетворень будемо розуміти
будь-яку підгрупу групи 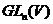 .
.
Проективність простору  є по визначенню проективність цього простору
на себе. Множина проективностей простору
є по визначенню проективність цього простору
на себе. Множина проективностей простору  - підгрупа групи підстановок множини
- підгрупа групи підстановок множини 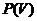 , що ми будемо називати
загальною групою проективностей простору
, що ми будемо називати
загальною групою проективностей простору  . Застосування риси індуцирує гомоморфізм
. Застосування риси індуцирує гомоморфізм
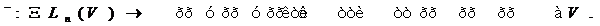
Іноді ми будемо використовувати 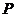 замість
замість 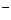 , думаючи
, думаючи 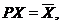 для образа
для образа
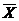 підмножини
підмножини 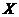 із
із 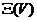 при
при 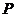 . Зокрема,
. Зокрема, 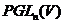 і
і 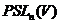 - підгрупи групи проективностей простору
- підгрупи групи проективностей простору  , вони називаються проективною
загальною лінійною групою й проективною спеціальною лінійною групою простору
, вони називаються проективною
загальною лінійною групою й проективною спеціальною лінійною групою простору  .
.
Було доведено, що 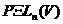 збігається із групою всіх проективностей простору
збігається із групою всіх проективностей простору
 , тому ми використовуємо
це позначення для обох груп. Під групою проективностей простору
, тому ми використовуємо
це позначення для обох груп. Під групою проективностей простору  будемо розуміти будь-яку підгрупу
групи
будемо розуміти будь-яку підгрупу
групи 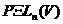 , а під проективною
групою лінійних перетворень простору
, а під проективною
групою лінійних перетворень простору  - будь-яку підгрупу групи
- будь-яку підгрупу групи 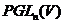 .
.
Для кожного ненульового елемента 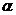 з
з 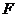 визначимо лінійне перетворення
визначимо лінійне перетворення 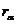 , думаючи
, думаючи 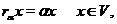 Ясно, що
Ясно, що 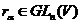 . Перетворення
. Перетворення  з
з 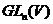 виду
виду 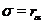 для якогось
для якогось 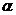 будемо називати розтяганням простору
будемо називати розтяганням простору  .
.
Множина розтягань простору  є нормальною підгрупою групи
є нормальною підгрупою групи 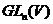 , що буде позначатися
через
, що буде позначатися
через 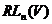 . Очевидно,
має місце ізоморфізм
. Очевидно,
має місце ізоморфізм 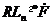 . Мають місце наступні дві пропозиції.
. Мають місце наступні дві пропозиції.
Пропозиція 27 Елемент  групи
групи 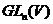 тоді й тільки тоді належить групі
тоді й тільки тоді належить групі 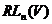 , коли
, коли 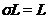 для всіх прямих
для всіх прямих 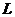 з
з  . Зокрема,
. Зокрема,
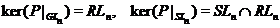
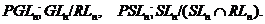
Пропозиція. 28 Централізатор у 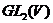 будь-якого елемента з
будь-якого елемента з 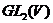 , що не є розтяганням, абелев.
, що не є розтяганням, абелев.
Нехай тепер  - регулярний знакозмінний простір. Тоді
- регулярний знакозмінний простір. Тоді  буде, звичайно, групою
геометричних перетворень простору
буде, звичайно, групою
геометричних перетворень простору  . Під групою симплектичних перетворень знакозмінного
простору
. Під групою симплектичних перетворень знакозмінного
простору  ми будемо
розуміти довільну підгрупу з
ми будемо
розуміти довільну підгрупу з  . Група
. Група 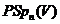 , одержувана із
, одержувана із  застосуванням гомоморфізму
застосуванням гомоморфізму 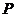 , називається проективної
симплектичною групою знакозмінного простору
, називається проективної
симплектичною групою знакозмінного простору  . Під проективною групою симплектичних перетворень
простору
. Під проективною групою симплектичних перетворень
простору  будемо
розуміти будь-яку підгрупу групи
будемо
розуміти будь-яку підгрупу групи 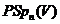 .
.
Пропозиція 29 Якщо  - ненульовий регулярний знакозмінний простір, те
- ненульовий регулярний знакозмінний простір, те
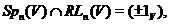
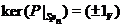
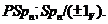
Доказ є легкою вправою й тому опускається.
Пропозиція 30 Якщо  - регулярний знакозмінний простір і
- регулярний знакозмінний простір і 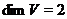 , те
, те 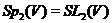 .
.
Доказ. Взявши симплектичну базу простору 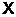 , за допомогою без праці переконуємося, що елемент
, за допомогою без праці переконуємося, що елемент  із
із 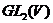 тоді й тільки тоді лежить в
тоді й тільки тоді лежить в 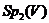 , коли
, коли 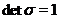 .
.
Полярністю абстрактного векторного простору  над полем
над полем 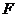 називається біекция
називається біекция
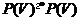 ,
, 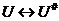 , така, що 1)
, така, що 1) 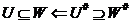 , 2)
, 2) 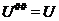 для всіх
для всіх  ,
, 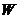 з
з 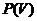 . Якщо
. Якщо  - регулярний знакозмінний простір над
- регулярний знакозмінний простір над 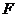 , те, мабуть,
, те, мабуть, 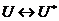 - полярність; вона
називається полярністю, певною знакозмінною формою
- полярність; вона
називається полярністю, певною знакозмінною формою 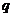 , наявної на
, наявної на  .
.
Пропозиція 31 Нехай  - абстрактний векторний простір над полем
- абстрактний векторний простір над полем 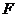 і
і 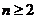 . Припустимо, що
. Припустимо, що  - регулярний знакозмінний
простір щодо кожної із двох знакозмінних форм
- регулярний знакозмінний
простір щодо кожної із двох знакозмінних форм 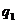 і
і 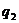 . Форми
. Форми 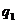 й
й 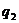 тоді й тільки тоді визначають ту саму полярність,
коли найдеться такий ненульовий елемент
тоді й тільки тоді визначають ту саму полярність,
коли найдеться такий ненульовий елемент 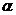 із
із 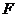 , що
, що 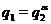 .
.
Доказ. Якщо 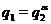 , то твердження очевидно. Залишається довести зворотне
твердження. Тому що
, то твердження очевидно. Залишається довести зворотне
твердження. Тому що  регулярно відносно
регулярно відносно 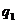 й
й 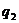 , те через і асоційовані лінійні відображення
, те через і асоційовані лінійні відображення 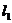 й
й 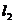 біективні, тобто
біективні, тобто 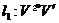 й
й 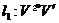 . З і припущення про те, що
. З і припущення про те, що 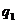 й
й 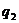 визначають ту саму полярність, треба, що
визначають ту саму полярність, треба, що 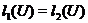 для всіх підпросторів
для всіх підпросторів
 з
з  . Отже,
. Отже, 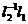 - елемент групи
- елемент групи 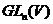 , щодо якого інваріантні
всі підпростори з
, щодо якого інваріантні
всі підпростори з  , Зокрема, щодо нього інваріантні всі прямі з
, Зокрема, щодо нього інваріантні всі прямі з  . Виходить, через
. Виходить, через 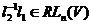 . Інакше
кажучи, найдеться такий ненульовий елемент
. Інакше
кажучи, найдеться такий ненульовий елемент 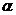 із
із 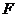 , що
, що 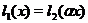 для всіх
для всіх 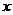 з
з  . Але тоді
. Але тоді 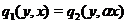 для всіх
для всіх 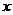 з
з  . Тому
. Тому 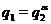 .
.
Пропозиція 32 Якщо поле 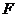 нескінченно, те групи
нескінченно, те групи 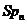 ,
, 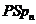 над
над 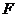 також нескінченні.
також нескінченні.
Доказ. Число трансвекцій 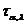 з
з  нескінченно.
нескінченно.
Теорема 33 Порядок групи 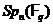 дорівнює
дорівнює
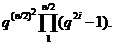
Порядок групи 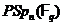 дорівнює
дорівнює
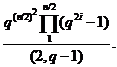
Доказ. Друге твердження треба з першого, тому що група
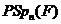 ізоморфна групі
ізоморфна групі
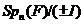 . Доведемо перше
твердження індукцією по
. Доведемо перше
твердження індукцією по 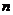 . Якщо
. Якщо 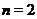 , то
, то 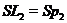 й можна вважати
й можна вважати 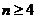 .
.
Під парою будемо розуміти впорядковану пару векторів 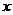 ,
, 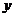 , таку, що
, таку, що 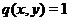 . Якщо
. Якщо 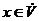 фіксовано, то існує єдина пара
фіксовано, то існує єдина пара
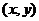 , де
, де 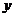 належить даній прямій,
не ортогональної к.
належить даній прямій,
не ортогональної к.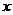 Тому число пар з
Тому число пар з 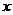 на першому місці дорівнює числу прямих,
що не лежать в
на першому місці дорівнює числу прямих,
що не лежать в 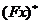 ,
тобто
,
тобто
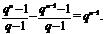
Таким чином, є 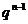 пара з
пара з 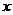 на першому місці, а всього
на першому місці, а всього 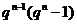 пара.
пара.
Зафіксуємо яку-небудь пару 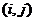 . По теоремі Витта для кожної пари
. По теоремі Витта для кожної пари 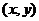 найдеться принаймні
один елемент групи
найдеться принаймні
один елемент групи  , що переводить
, що переводить 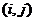 в.
в. 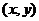 Отже, є точно
Отже, є точно
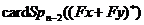
елементів з  , що переводять пари
, що переводять пари 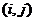 в парі
в парі 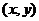 . По припущенню індукції це число дорівнює
. По припущенню індукції це число дорівнює
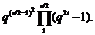
Далі, кожний елемент групи  переводить
переводить 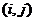 точно в одну пару. Отже, група
точно в одну пару. Отже, група  містить
містить
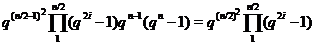
елементів, що й було потрібно довести.
Пропозиція 34Якщо 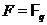 , те число максимальних цілком вырожденных підпросторів
простору
, те число максимальних цілком вырожденных підпросторів
простору  дорівнює
дорівнює
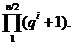
Доказ.1) Покажемо спочатку, що підгрупа 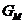 групи
групи  , що залишає на місці
довільне максимальне цілком вироджений підпростір
, що залишає на місці
довільне максимальне цілком вироджений підпростір 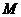 простору
простору  , має порядок
, має порядок
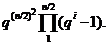
Щоб переконатися в цьому, зафіксуємо симплектичну базу
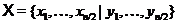
простору  , у якій вектори
, у якій вектори 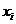 породжують
породжують 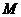 . Із треба, що матриця довільного перетворення
. Із треба, що матриця довільного перетворення 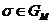 має вигляд
має вигляд
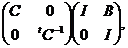
де 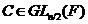 , а
, а 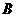 - симетрична матриця порядку
- симетрична матриця порядку 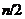 над
над 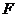 ; ці
; ці 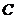 й
й 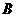 визначаються перетворенням
визначаються перетворенням  однозначно. Крім того, будь-які
такі
однозначно. Крім того, будь-які
такі 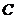 й
й 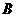 відповідають якомусь
відповідають якомусь
 із
із 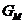 . Наше твердження виходить
тепер, якщо помножити порядок групи
. Наше твердження виходить
тепер, якщо помножити порядок групи 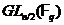 на число симетричних матриць порядку
на число симетричних матриць порядку 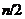 над полем
над полем 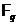 , тобто
, тобто 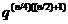 .
.
2) Зафіксуємо максимальне цілком вироджений підпростір
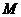 простору
простору  . По теоремі Витта всі
максимальні цілком выроджені підпростору простору
. По теоремі Витта всі
максимальні цілком выроджені підпростору простору  даються формулою
даються формулою 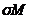 , де
, де  пробігає групу
пробігає групу  . Із зауваження 1) легко треба,
що в цьому процесі кожне максимальне цілком вироджений підпростір повторюється точно
. Із зауваження 1) легко треба,
що в цьому процесі кожне максимальне цілком вироджений підпростір повторюється точно
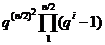
раз, тому загальне число таких підпросторів дорівнює порядку
групи  , діленому
на зазначену величину. Очевидно, це і є необхідне число.
, діленому
на зазначену величину. Очевидно, це і є необхідне число.
Пропозиція 35 Якщо 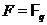 , те число регулярних площин у просторі
, те число регулярних площин у просторі  дорівнює
дорівнює
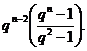
Доказ. Надходячи, як при доказі твердження , переконаємося, що  повинне містити
повинне містити
регулярних площин. Це число збігається із зазначеним вище
(застосувати теорему ).
Пропозиція 36 Група 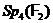 ізоморфна симетричній групі
ізоморфна симетричній групі 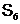 .
.
Доказ. Будемо називати конфігурацією довільна підмножина
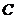 з
з 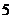 елементів в
елементів в 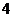 - мірному регулярному
знакозмінному просторі
- мірному регулярному
знакозмінному просторі  над полем
над полем 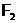 , що володіє тим властивістю, що будь-які два його
різних елементи не ортогональні. Кожний ненульовий вектор
, що володіє тим властивістю, що будь-які два його
різних елементи не ортогональні. Кожний ненульовий вектор 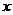 з
з  належить рівно двом конфігураціям
належить рівно двом конфігураціям 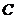 і
і 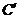 , так що вони перетинаються по
, так що вони перетинаються по
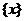 . Щоб переконатися
в цьому, візьмемо симплектическую базу
. Щоб переконатися
в цьому, візьмемо симплектическую базу 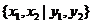 простору
простору  , у якій
, у якій 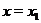 . Ясно, що
. Ясно, що
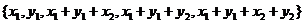
і
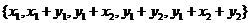
дві різні конфігурації, що перетинаються по множині 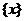 . Легка перевірка перебором
показує, що інших конфігурацій, що містять елемент
. Легка перевірка перебором
показує, що інших конфігурацій, що містять елемент 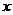 , немає. Якщо тепер виписати всі різні
конфігурації
, немає. Якщо тепер виписати всі різні
конфігурації 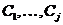 в
просторі
в
просторі  , то кожний
вектор
, то кожний
вектор 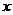 із
із 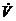 з'явиться точно у двох
з них, звідки
з'явиться точно у двох
з них, звідки 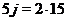 й
й
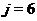 . Нехай
. Нехай 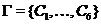 - Множина всіх конфігурацій
в.
- Множина всіх конфігурацій
в.
Якщо  - довільний елемент із
- довільний елемент із 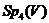 , то
, то 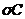 тоді й тільки тоді є конфігурацією, коли
тоді й тільки тоді є конфігурацією, коли
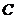 - конфігурація,
тому
- конфігурація,
тому  індуцирує
відображення
індуцирує
відображення 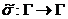 .
Ясно, що це відображення на й, виходить, перестановка на
.
Ясно, що це відображення на й, виходить, перестановка на 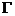 . Очевидно, що
. Очевидно, що 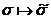 є гомоморфне відображення
є гомоморфне відображення
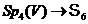 . Щоб знайти його
ядро, візьмемо в
. Щоб знайти його
ядро, візьмемо в 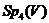 елемент
елемент 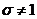 . Нехай
. Нехай 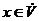 такий, що
такий, що 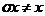 . Нехай
. Нехай 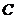 і
і 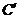 - дві конфігурації, що містять
- дві конфігурації, що містять 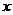 . Тоді
. Тоді 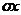 не належить однієї з них, скажемо,
не належить однієї з них, скажемо,
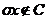 . Звідси
. Звідси 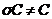 й
й 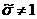 . Інакше кажучи, ядро тривіально,
і ми маємо інективный гомоморфізм
. Інакше кажучи, ядро тривіально,
і ми маємо інективный гомоморфізм 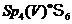 . По теоремі група
. По теоремі група 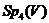 складається
з
складається
з 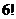 елементів, тому
елементів, тому
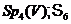 .
.
Помітимо, що група 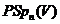 неабелева. Щоб переконатися в цьому, досить взяти
нетривіальні проективні трансвекції із
неабелева. Щоб переконатися в цьому, досить взяти
нетривіальні проективні трансвекції із 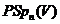 із прямими. Отже, група
із прямими. Отже, група  також неабелева.
також неабелева.
Пропозиція 37 Група 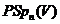 має тривіальний центр, а
має тривіальний центр, а 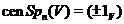 .
.
Доказ. Розглянемо довільний елемент  із центра групи
із центра групи 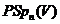 . Нехай
. Нехай 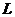 - довільна пряма з
- довільна пряма з
 . Нехай
. Нехай 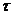 - проективна трансвекція
із
- проективна трансвекція
із 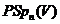 із прямій
із прямій 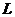 . Тоді прямій перетворення
. Тоді прямій перетворення
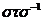 є
є 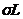 . Але
. Але 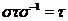 , тому що
, тому що  лежить у центрі. Отже,
лежить у центрі. Отже,
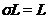 для всіх
для всіх 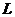 . Тому
. Тому 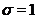 й, виходить, група
й, виходить, група
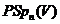 дійсно не має
центра. Друге твердження треба з першого, якщо застосувати гомоморфізм
дійсно не має
центра. Друге твердження треба з першого, якщо застосувати гомоморфізм 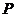 .
.
Пропозиція 38 Якщо 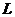 ,
, 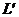 - довільні прямі з
- довільні прямі з  , та множина трансвекцій із
, та множина трансвекцій із  із прямої
із прямої 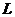 й множину трансвекцій
з прямій
й множину трансвекцій
з прямій 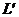 сполучені
відносно
сполучені
відносно  .
.
Доказ. По теоремі Витта в групі  існує такий елемент
існує такий елемент 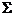 , що
, що 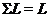 . Тоді сполучення елементом
. Тоді сполучення елементом 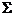 відображає множина
трансвекцій із
відображає множина
трансвекцій із  із
прямій
із
прямій 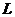 на множину
трансвекцій із
на множину
трансвекцій із  із
прямій
із
прямій 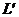 .
.
Приклад 39 Дві трансвекції з  не обов'язково сполучені в.
не обов'язково сполучені в.  Наприклад, трансвекції
з прямій
Наприклад, трансвекції
з прямій 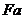 , сполучені
з
, сполучені
з 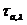 , мають вигляд
, мають вигляд
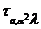 , де
, де 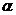 пробігає
пробігає 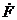 .
.
Зауваження 40 Нехай 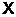 - симплектическая база простору
- симплектическая база простору  . Якщо
. Якщо 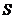 - довільна симетрична матриця
порядку
- довільна симетрична матриця
порядку 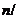 2 над
2 над 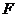 і
і  - лінійне перетворення, певне
матрицею
- лінійне перетворення, певне
матрицею 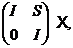 те ми знаємо, що
те ми знаємо, що  належить групі
належить групі  . Якщо перетворити
. Якщо перетворити 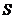 в
в 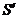 , роблячи 1) додаток кратного одного стовпця
до іншого з наступним аналогічним перетворенням відповідних рядків або 2) перестановку
двох стовпців з наступною перестановкою відповідних рядків, то лінійне перетворення
, роблячи 1) додаток кратного одного стовпця
до іншого з наступним аналогічним перетворенням відповідних рядків або 2) перестановку
двох стовпців з наступною перестановкою відповідних рядків, то лінійне перетворення
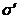 з матрицею
з матрицею 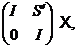 знову буде належати групі
знову буде належати групі  , тому що
, тому що 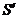 теж буде симетричною. У дійсності
теж буде симетричною. У дійсності
 й
й 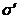 сполучені в.
сполучені в.  Щоб переконатися в
цьому, помітимо, що
Щоб переконатися в
цьому, помітимо, що 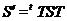 при підходящій матриці
при підходящій матриці 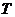 з
з 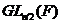 . Перетворення
. Перетворення 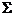 , певне матрицею
, певне матрицею 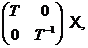 належить групі
належить групі  , і
, і 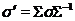 , тому що
, тому що 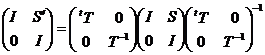 .
.
Пропозицію 41 Припустимо, що 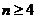 ,
, 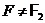 ,
, 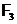 і нехай
і нехай  - нормальна підгрупа групи
- нормальна підгрупа групи  , що містить регулярний елемент
, що містить регулярний елемент
 із відрахуванням
із відрахуванням
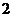 , у вигляді добутку
двох трансвекцій з
, у вигляді добутку
двох трансвекцій з  . Тоді
. Тоді 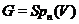 .
.
Доказ. Маємо розкладання 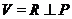 , де
, де 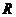 - регулярна площина. Розглянемо групу
- регулярна площина. Розглянемо групу
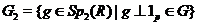
Тоді 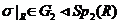 . Крім того,
. Крім того, 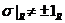 . Це очевидно, якщо
. Це очевидно, якщо 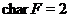 ; якщо ж
; якщо ж 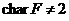 , те застосовуємо 2.1.12 і теорему 2.1.11
. Тому
, те застосовуємо 2.1.12 і теорему 2.1.11
. Тому 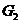 - нормальна підгрупа в
- нормальна підгрупа в 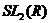 , що не втримується в.
, що не втримується в. 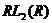 Звідси треба, що
Звідси треба, що 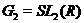 . Зокрема, якщо
. Зокрема, якщо 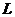 - фіксована пряма в
- фіксована пряма в
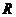 , те
, те 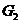 містить всі трансвекції
площини
містить всі трансвекції
площини 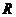 з прямій
з прямій
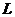 . Отже,
. Отже,  містить всі трансвекції
із
містить всі трансвекції
із  із прямій
із прямій 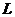 , а тому в силу взагалі всі трансвекції з
, а тому в силу взагалі всі трансвекції з  і
і 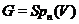 .
.
Пропозицію 42 Припустимо, що 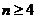 ,
, 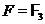 або
або 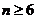 ,
, 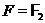 , і нехай
, і нехай  - нормальна підгрупа групи
- нормальна підгрупа групи  , що містить елемент
, що містить елемент  із відрахуванням 2,
у вигляді добутку двох трансвекцій з
із відрахуванням 2,
у вигляді добутку двох трансвекцій з  . Тоді
. Тоді 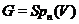 .
.
Доказ.1) Модифікація міркувань, використаних при доказі
твердження , дозволяє вважати, що 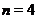 , якщо
, якщо 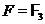 , і
, і 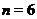 , якщо
, якщо 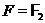 .
.
2) Розглянемо спочатку випадок 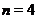 ,
, 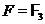 . Тоді
. Тоді  має вигляд
має вигляд 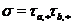 , причому
, причому 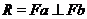 , а зірочки рівні
, а зірочки рівні 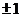 . Далі ці трансвекції перестановочні,
тому що
. Далі ці трансвекції перестановочні,
тому що 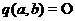 , тому
ми можемо, якщо потрібно, замінити
, тому
ми можемо, якщо потрібно, замінити  на
на 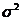 й уважати, що насправді
й уважати, що насправді 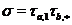 . Можна вважати, що ця нова
. Можна вважати, що ця нова 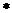 є
є  . Справді, якщо
. Справді, якщо 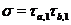 , те за допомогою теореми
Витта виберемо таке
, те за допомогою теореми
Витта виберемо таке 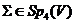 , що
, що 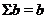 ,
, 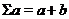 . Тоді
. Тоді 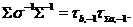 .
Замінимо тепер
.
Замінимо тепер  на
на 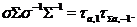 . Отже, можна вважати, що
. Отже, можна вважати, що 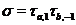 . Доповнимо
. Доповнимо 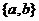 до симплектичної бази
до симплектичної бази
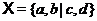
простору  й помітимо, що
й помітимо, що
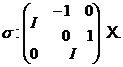
Підходящим сполученням ми можемо знайти в  лінійні перетворення
з матрицями
лінійні перетворення
з матрицями
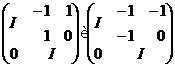
у базі 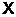 . Добуток цих перетворень дорівнює елементу із
. Добуток цих перетворень дорівнює елементу із  із матрицею
із матрицею
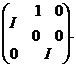
Отже, група  містить
містить 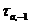 . Таким чином, вона містить всі (= обидві) трансвекції
із
. Таким чином, вона містить всі (= обидві) трансвекції
із 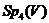 із прямій
із прямій 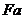 . Через звідси треба, що
. Через звідси треба, що  містить всі трансвекції з
містить всі трансвекції з 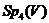 і, виходить,
і, виходить, 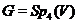 .
.
3) Нехай тепер 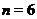 ,
, 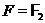 . Тоді
. Тоді 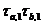 й
й 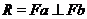 . Доповнимо
. Доповнимо 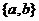 до симплектичної бази
до симплектичної бази 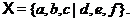 Тоді
Тоді
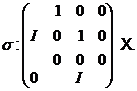
Сполучення дає нам у  лінійні перетворення з матрицями
лінійні перетворення з матрицями
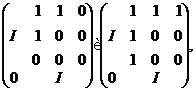
а тому й з матрицями
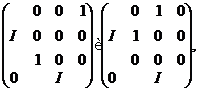
а виходить, і з матрицею
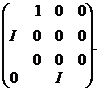
Інакше кажучи,  містить
містить 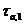 і, отже, всі трансвекції з
і, отже, всі трансвекції з  , звідки
, звідки 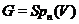 . Пропозиція 43 Якщо
. Пропозиція 43 Якщо 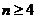 , те
, те 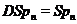 за одним виключенням:
за одним виключенням: 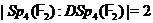 . Доказ. Нехай
. Доказ. Нехай 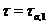 , для якогось
, для якогось 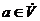 . По теоремі Витта існує таке
. По теоремі Витта існує таке 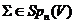 , що
, що 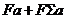 - площина й
- площина й 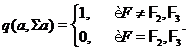
Покладемо
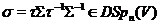
Залишилося застосувати й . У винятковому випадку застосовуємо й добре відомі властивості групи 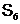 .
.
Пропозиція 44 Якщо 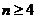 , те
, те 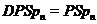 за одним виключенням:
за одним виключенням: 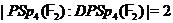 .
.
Теорема 45 Для будь-якого парного числа 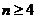 й кожного поля
й кожного поля 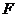 група
група 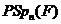 проста за винятком
групи
проста за винятком
групи 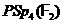 , що простій
не є.
, що простій
не є.
Доказ.1) Виняткове поводження групи 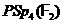 треба з . Будемо припускати тому, що
треба з . Будемо припускати тому, що 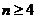 в загальному випадку й
в загальному випадку й 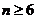 при
при 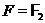 . Замість проективної групи ми будемо
мати справу із групою
. Замість проективної групи ми будемо
мати справу із групою 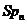 . Досить розглянути нормальну підгрупу
. Досить розглянути нормальну підгрупу  групи
групи 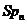 , що не втримується
в підгрупі
, що не втримується
в підгрупі 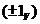 , і
довести, що
, і
довести, що 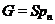 .
.
2) Спочатку покажемо, що є 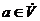 ,
, 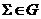 , такі, що
, такі, що 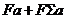 - регулярна площина. Для цього візьмемо в групі
- регулярна площина. Для цього візьмемо в групі
 елемент.
елемент. 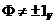
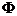 зрушує принаймні одну пряму
з
зрушує принаймні одну пряму
з  , тобто існує
така пряма
, тобто існує
така пряма 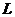 з
з  , що
, що 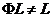 . Нехай
. Нехай 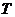 - нетривіальна трансвекция із
- нетривіальна трансвекция із
 із прямій
із прямій 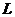 . Тоді елемент
. Тоді елемент 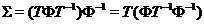 належить групі
належить групі  і є добутком двох трансвекцій
із
і є добутком двох трансвекцій
із  із різними
прямими
із різними
прямими 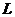 й
й 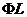 . Тому простір перетворення
. Тому простір перетворення
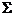 є площина
є площина 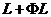 , зокрема,
, зокрема, 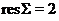 . Якщо
. Якщо 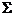 - гіперболічне перетворення,
то
- гіперболічне перетворення,
то 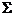 - інволюція.
Застосуємо тепер твердження 1.18, якщо характеристика дорівнює
- інволюція.
Застосуємо тепер твердження 1.18, якщо характеристика дорівнює 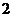 , і твердження 1.13, якщо характеристика
не дорівнює
, і твердження 1.13, якщо характеристика
не дорівнює 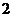 . Тоді,
зокрема, ми одержимо, що
. Тоді,
зокрема, ми одержимо, що 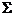 не є добутком
не є добутком 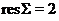 трансвекції з
трансвекції з  , що суперечить допущенню. Отже,
, що суперечить допущенню. Отже,
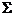 не може бути гіперболічним.
Виходить, існує такий вектор
не може бути гіперболічним.
Виходить, існує такий вектор 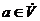 , що
, що 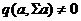 , тобто
, тобто 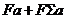 - регулярна площина.
- регулярна площина.
3) Можна також показати, що є вектор 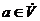 і перетворення
і перетворення 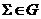 , такі, що
, такі, що 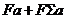 - вироджена площина.
Справді, візьмемо в
- вироджена площина.
Справді, візьмемо в  елемент
елемент 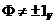 . Існує такий вектор
. Існує такий вектор 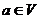 , що
, що 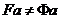 .
.
Якщо 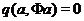 , то ціль досягнута, тому будемо вважати, що
, то ціль досягнута, тому будемо вважати, що 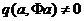 .
.
Виберемо 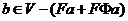 так, щоб було
так, щоб було
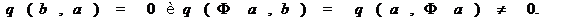
По теоремі Витта в  найдеться перетворення
найдеться перетворення 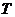 , таке, що
, таке, що 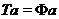 ,
, 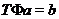 . Тоді перетворення
. Тоді перетворення 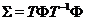 належить
належить  і переводить
і переводить 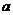 в
в 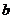 , тому
, тому 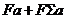 - вироджена площина.
- вироджена площина.
4) Візьмемо 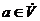 ,
, 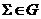 так, щоб площина
так, щоб площина 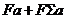 була регулярної при
була регулярної при 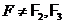 й виродженій при
й виродженій при 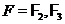 . Тоді перетворення
. Тоді перетворення
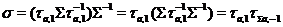
належить групі  , є добутком двох трансвекцій з
, є добутком двох трансвекцій з  і його простір є площина
і його простір є площина 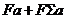 . Тому
. Тому 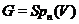 .
.
Пропозиція 46 Якщо 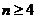 й
й 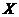 - нормальна підгрупа групи
- нормальна підгрупа групи 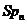 , те
, те 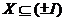 або
або 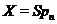 , за винятком групи
, за винятком групи 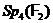 , що, мабуть, не має цю властивість.
, що, мабуть, не має цю властивість.
Доказ. Із приводу виключення див. . Далі, застосовуючи до 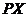 теорему , одержимо, що
теорему , одержимо, що 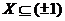 або
або 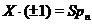 . Допустимо останнє. Тоді
. Допустимо останнє. Тоді
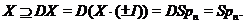
Пропозиція доведена.
Теорему про простоту можна також довести, використовуючи
групи підстановок. Нагадаємо, що групою підстановок непустої множини 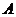 називається підгрупа
називається підгрупа
 групи всіх підстановок
множини
групи всіх підстановок
множини 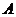 . Далі,
. Далі,
 називається транзитивної,
якщо для будь-яких
називається транзитивної,
якщо для будь-яких 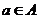 ,
, 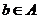 існує така підстановка
існує така підстановка  з
з  , що
, що 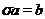 . Нагадаємо, що розбивкою множини
. Нагадаємо, що розбивкою множини 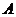 називається множина
називається множина
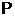 попарно непересічних
підмножин, об'єднання яких дорівнює
попарно непересічних
підмножин, об'єднання яких дорівнює 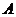 . Тривіальними називаються дві розбивки, що складаються
відповідно із самого
. Тривіальними називаються дві розбивки, що складаються
відповідно із самого 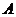 й із всіх одноелементних підмножин. Транзитивна
група
й із всіх одноелементних підмножин. Транзитивна
група  підстановок
множини
підстановок
множини 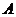 , якщо
існує така нетривіальна розбивка
, якщо
існує така нетривіальна розбивка 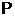 множини
множини 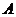 , що
, що 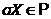 для всіх
для всіх 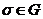 ,
, 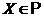 . У противному випадку група називається примітивної.
Наступний результат є тут ключовим.
. У противному випадку група називається примітивної.
Наступний результат є тут ключовим.
Пропозиція 47 Примітивна група підстановок  множини
множини 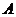 проста, якщо виконані наступні
умови:
проста, якщо виконані наступні
умови:
1) 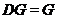 ,
,
2) для якогось 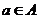 стабілізатор
стабілізатор 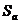 містить таку нормальну абелеву підгрупу
містить таку нормальну абелеву підгрупу 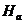 , що
, що  породжується підгрупами
породжується підгрупами 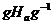 ,
, 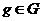 .
.
Для доказу теореми з використанням цього результату розглянемо 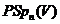 як групу підстановок множини прямі
як групу підстановок множини прямі 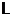 простори
простори  . Це можливо через те,
що
. Це можливо через те,
що 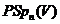 , будучи підгрупою
групи проективностей простору
, будучи підгрупою
групи проективностей простору  , точно діє на
, точно діє на 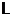 й, виходить,
й, виходить, 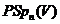 природно ізоморфна групі підстановок
множини
природно ізоморфна групі підстановок
множини 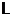 . Ми знаємо,
що група
. Ми знаємо,
що група 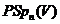 транзитивна
(теорема Витта),
транзитивна
(теорема Витта), 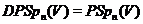 (див. ) і, нарешті, множина
проективних трансвекцій із
(див. ) і, нарешті, множина
проективних трансвекцій із 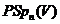 із прямій
із прямій 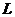 разом з тотожним перетворенням утворить нормальну
абелеву підгрупу стабілізатора прямій
разом з тотожним перетворенням утворить нормальну
абелеву підгрупу стабілізатора прямій 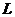 в
в 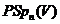 , що разом зі своїми сполученими в
, що разом зі своїми сполученими в 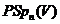 породжує групу
породжує групу 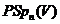 . Тому все, що залишилося
зробити, перш ніж послатися на , - це перевірити, що група
. Тому все, що залишилося
зробити, перш ніж послатися на , - це перевірити, що група
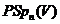 примітивна.
примітивна.
Пропозиція 48 При 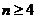 група
група 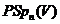 підстановок множини
підстановок множини 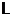 прямі простори
прямі простори  примітивна.
примітивна.
Доказ.1) Розглянемо розбивку 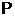 множини
множини 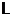 , що містить принаймні дві підмножини,
одне із яких, скажемо
, що містить принаймні дві підмножини,
одне із яких, скажемо 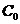 , містить не менш двох прямих. Нам потрібно знайти
елемент групи
, містить не менш двох прямих. Нам потрібно знайти
елемент групи 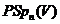 ,
що не зберігає цю розбивку. Допустимо, що такого елемента не існує.
,
що не зберігає цю розбивку. Допустимо, що такого елемента не існує.
2) Нехай спочатку 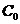 містить дві різні не ортогональні прямі
містить дві різні не ортогональні прямі 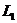 ,
, 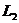 . Тоді кожні дві різні прямі
. Тоді кожні дві різні прямі
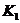 ,
, 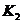 з
з 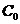 повинні бути не ортогональні.
Справді, якщо це не так, то найдуться різні
повинні бути не ортогональні.
Справді, якщо це не так, то найдуться різні 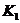 ,
, 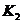 з
з 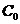 , такі, що
, такі, що 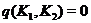 . Візьмемо пряму
. Візьмемо пряму 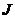 з
з  , не приналежній підмножині
, не приналежній підмножині 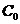 . Якщо
. Якщо 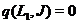 , то по теоремі Витта існує таке
перетворення
, то по теоремі Витта існує таке
перетворення 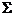 з
з
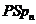 , що
, що 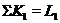 ,
, 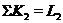 , і, отже, воно порушує розбивку.
Якщо
, і, отже, воно порушує розбивку.
Якщо 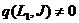 , то знову
по теоремі Витта є таке
, то знову
по теоремі Витта є таке 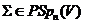 , що
, що 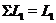 ,
, 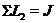 і, виходить,
і, виходить, 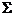 знову порушує розбивка. Отже, ніякі дві різні прямі
з
знову порушує розбивка. Отже, ніякі дві різні прямі
з 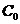 не є ортогональними.
Тільки що проведені міркування показують, що якщо
не є ортогональними.
Тільки що проведені міркування показують, що якщо 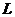 - довільна пряма з
- довільна пряма з 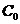 , те
, те 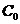 містить всі прямі з
містить всі прямі з  , не ортогональні к.
, не ортогональні к.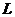 Тепер очевидно, що
можна знайти в
Тепер очевидно, що
можна знайти в  пряму
пряму
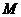 , не ортогональну
до
, не ортогональну
до 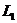 , але ортогональну
до
, але ортогональну
до 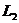 тоді перша
умова спричиняє, що
тоді перша
умова спричиняє, що 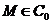 , а друге - що
, а друге - що 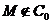 , - протиріччя.
, - протиріччя.
3) Ми можемо, таким чином, уважати, що всі прямі з 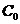 попарно ортогональні.
Міркування, використані в п.2), показують тоді, що якщо
попарно ортогональні.
Міркування, використані в п.2), показують тоді, що якщо 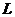 - довільна пряма з
- довільна пряма з 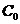 , те
, те 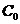 містить всі прямі, ортогональні до
містить всі прямі, ортогональні до 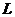 , а це неможливо. Пропозиція
доведена.
, а це неможливо. Пропозиція
доведена.
Нехай  - кінцева група,
- кінцева група, 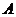 і
і 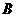 - підгрупи групи
- підгрупи групи  . Будемо говорити, що група
. Будемо говорити, що група  допускає факторізацію
допускає факторізацію
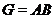 , якщо для всякого
, якщо для всякого
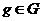 має місце рівність
має місце рівність
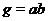 , де
, де 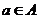 ,
, 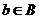 . Факторізація називається максимальної,
якщо
. Факторізація називається максимальної,
якщо 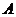 й
й 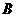 максимальні підгрупи
в групі
максимальні підгрупи
в групі  . Ми розглянемо
максимальні факторізації симплектичної групи
. Ми розглянемо
максимальні факторізації симплектичної групи 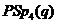 , певної над кінцевим полем
, певної над кінцевим полем 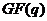 .
.
Нехай 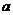 і
і 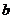 - цілі числа,
- цілі числа, 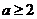 ,
, 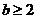 . Якщо
. Якщо 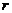 - просте число, що ділить
- просте число, що ділить 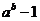 і не ділить числа
і не ділить числа 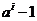 для
для 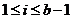 , то
, то 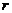 називають примітивним простим дільником
числа
називають примітивним простим дільником
числа 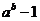 .
.
Добре відомо, що при 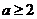 ,
, 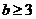 і
і 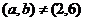 завжди є примітивний простий дільник числа
завжди є примітивний простий дільник числа 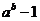 . Нехай
. Нехай 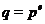 , де
, де 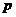 - просте число,
- просте число, 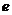 - ціле позитивне число.
Позначимо
- ціле позитивне число.
Позначимо 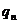 найбільший
примітивний простий дільник числа
найбільший
примітивний простий дільник числа 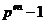 (так, що
(так, що 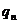 ділить
ділить 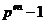 і не ділить
і не ділить 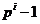 для
для 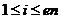 ). Визначимо
). Визначимо 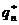 як добуток всіх примітивних простих дільників
як добуток всіх примітивних простих дільників 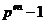 . Ми будемо розглядати
максимальні факторізації групи
. Ми будемо розглядати
максимальні факторізації групи 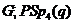 . Відзначимо, що
. Відзначимо, що
Теорема. 49Нехай 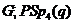 , де
, де 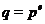 - непарне число. Якщо
- непарне число. Якщо 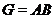 , де
, де 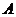 й
й 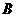 - максимальні підгрупи групи
- максимальні підгрупи групи  , тоді
, тоді 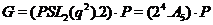 , де
, де 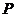 - максимальна параболічна підгрупа
групи
- максимальна параболічна підгрупа
групи  , ізоморфна
, ізоморфна
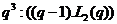 й, яка має порядок
й, яка має порядок
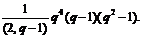
Доказ. Припустимо, що 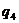 ділить
ділить 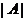 . Із треба, що
. Із треба, що 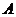 є однієї з наступних груп
є однієї з наступних груп 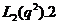 ,
, 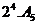 ,
, 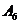 або
або 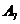 . Нехай спочатку
. Нехай спочатку 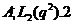 . У цьому випадку
. У цьому випадку 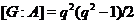 . Із треба, що
. Із треба, що 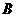 це в точності максимальна параболічна підгрупа
групи
це в точності максимальна параболічна підгрупа
групи 
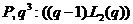 й
й 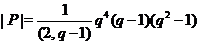 . З порівняння порядків групи
. З порівняння порядків групи
 й добутки
й добутки 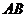 одержуємо наступну
максимальну факторізацію:
одержуємо наступну
максимальну факторізацію:
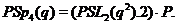
Нехай тепер 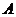 є однієї з наступних груп
є однієї з наступних груп 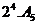 ,
, 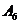 або
або 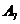 . Із сказаного вище випливає, що
. Із сказаного вище випливає, що 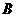 не ізоморфно
не ізоморфно 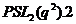 . З пункту 2.4 одержимо, що
. З пункту 2.4 одержимо, що 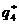 є
є 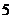 або
або 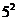 . По теоремі 2.4D
. По теоремі 2.4D 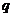 є 3 або
7. Якщо
є 3 або
7. Якщо 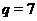 , тоді
5 ділить
, тоді
5 ділить 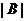 . У цьому
випадку із треба, що
. У цьому
випадку із треба, що 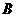 одна із груп
одна із груп 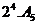 ,
, 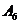 ,
, 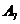 . Оскільки
. Оскільки 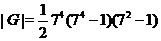 , те
, те 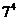 ділить
ділить 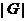 . Однак
. Однак 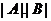 не ділиться на
не ділиться на 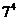 . Протиріччя з тим, що
. Протиріччя з тим, що 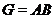 . Отже,
. Отже, 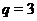 і
і 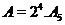 . Тому що 27 ділить
. Тому що 27 ділить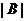 , то
, то 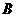 є параболічною підгрупою групи
є параболічною підгрупою групи  й має місце факторизация:
й має місце факторизация:
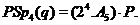
Теорема доведена.
Нехай 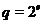 , де
, де 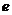 - позитивне число. Тоді ортогональна група
- позитивне число. Тоді ортогональна група 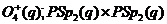 й
й 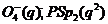 .
. 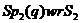 позначає сплетення групи
позначає сплетення групи 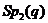 із групою
із групою 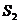 , тобто
, тобто 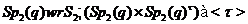 , де
, де 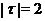 . Очевидно, що
. Очевидно, що 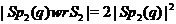 ;
; 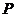 - максимальна параболічна підгрупа
в
- максимальна параболічна підгрупа
в 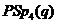 порядку
порядку 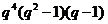 ;
; 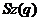 - група Судзуки порядку
- група Судзуки порядку 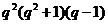 , де
, де 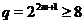 .
.
Лема 50 Нехай 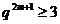 . Тоді
. Тоді
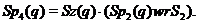
Доказ. Із треба, що 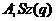 є максимальною підгрупою
в.
є максимальною підгрупою
в. 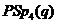 Нехай
Нехай 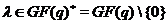 і
і 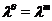 . Позначимо
. Позначимо
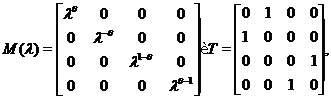
де 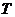 матриця в канонічному базисі симплектичного простору
матриця в канонічному базисі симплектичного простору
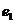 ,
, 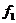 ,
, 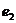 ,
, 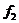 .
.
Тоді 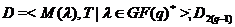 - група, що фіксує розкладання:
- група, що фіксує розкладання:
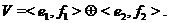
Із треба, що стабілізатор цього
розкладання 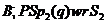 ,
,
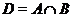 і
і 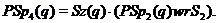 .
.
Лема доведена.
У наведених позначеннях з урахуванням таблиці 1 і леми одержимо:
Теорема 51 Нехай 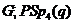 , де
, де 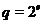 . Якщо
. Якщо 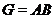 , де
, де 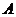 й
й 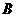 - максимальні підгрупи в групі
- максимальні підгрупи в групі  . Тоді
. Тоді
1) 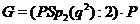 ,
,
2) 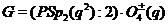 ,
,
3) 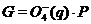 ,
,
4) 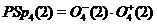 ,
,
5) 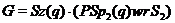 .
.
У дипломній роботі знайдені максимальні факторізації симплектичних
груп 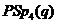 . Доведено
наступні теореми.
. Доведено
наступні теореми.
Теорема 1. Нехай 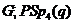 , де
, де 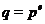 - непарне число. Якщо
- непарне число. Якщо 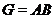 , де
, де 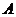 й
й 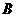 - максимальні підгрупи групи
- максимальні підгрупи групи  , тоді
, тоді 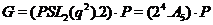 , де
, де 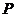 - максимальна параболічна підгрупа
групи
- максимальна параболічна підгрупа
групи  , ізоморфна
, ізоморфна
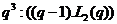 й має порядок
й має порядок
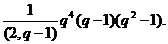
Теорема 2. Нехай 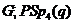 , де
, де 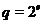 . Якщо
. Якщо 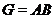 , де
, де 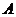 й
й 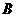 - максимальні підгрупи в групі
- максимальні підгрупи в групі  . Тоді
. Тоді
1) 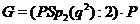 ,
,
2) 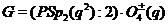 ,
,
3) 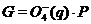 ,
,
4) 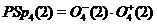 ,
,
5) 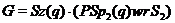 .
.
1.
Монахов В.С. Введення в теорію кінцевих груп і їхніх класів. - К., 2004
2.
Каргаполов М.І., Мерзляків Ю.И., Основи теорії груп. - К., 2004
3.
Хол Ф., Теорія груп. - К., 2003
4.
Горенстейн Д., Кінцеві прості групи: введення в їхню класифікацію., - К.,
2003
5.
Казарін Л.С., Факторізації кінцевих груп розв'язними підгрупами // Укр. мат.
журн. 1991. Т.43, N 7 - і 8. С.947 - і 950.
6.
Mitchel H.H., Determination of the finite quaternary linear
groups. Trans. Amer. Math. Soc. V.14, 1913. p.123--142.
7.
Liebek M.W., Praeqer C.E., Saxl J., The maximal factorizations
of the finite simple groups and their automorphism groups. Mem. Amer. Math.
Soc. V.86, N.432. p.1--151.
8.
Suzuki M., A new type of simple groups of finite
order. Proc. Nat. Acad. Sci. US 46, 1960. p.868--870.