Типовой расчет

Типовой расчет

1. Найти сумму ряда:

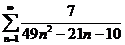
Решение.

Разложим знаменатель на множители.

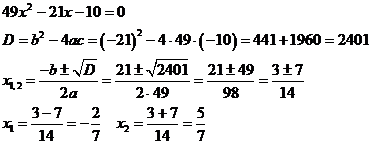
Значит,

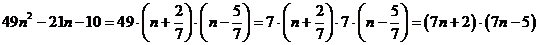
Разложим дробь 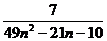, используя метод неопределённых коэффициентов.

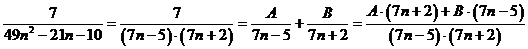
то есть:

, ,

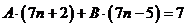
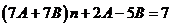
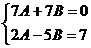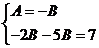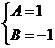
Следовательно,

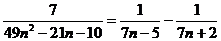
Тогда, исходный ряд примет вид:

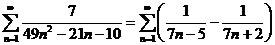
Найдём n – первые членов ряда, записывая дроби с одинаковыми знаменателями друг под другом:

=

=  

=

=  

=

=  

=  

=  

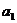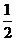
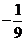
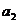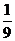
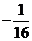
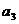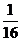
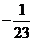
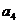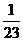
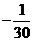
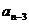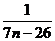
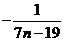
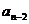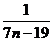
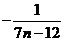
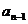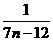
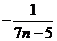
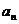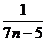
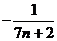
Сложим n – первых членов ряда и найдём их сумму.

.

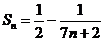Тогда искомая сумма равна:

.

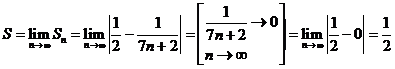Ответ: .

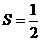2. Найти сумму ряда:

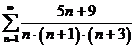
Решение.

Разложим дробь 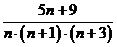, используя метод неопределённых коэффициентов.

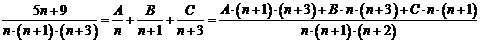
то есть:

, , ,

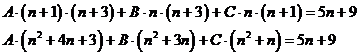
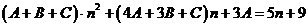
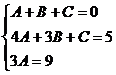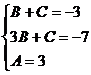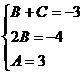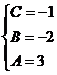
Следовательно,

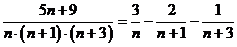
Тогда, исходный ряд примет вид:

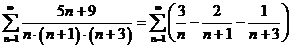
Найдём n – первых членов ряда 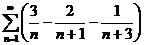, записывая дроби с одинаковыми знаменателями, друг под другом:

=  

=   

=   

=   

=   

=   

=   

=   

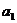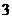
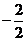
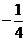
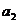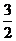
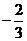
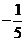
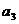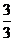
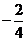
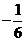
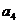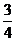
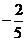
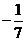
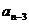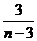
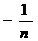
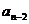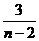
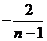
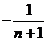
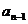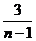
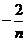
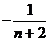
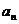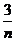
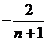
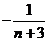
Сложим n – первых членов ряда

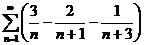
и найдём их сумму.

.

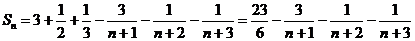Тогда искомая сумма равна:

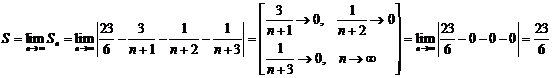
Ответ: .

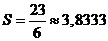3. Исследовать ряд на сходимость

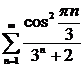
Решение.

Так как 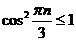, то рассмотрим ряд

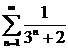, тогда

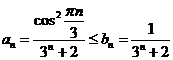
Воспользуемся признаком Даламбера.

,

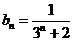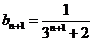
Тогда,

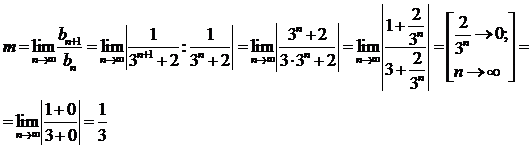
Ответ: Ряд 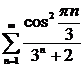 сходится.

4. Исследовать ряд на сходимость

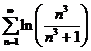
Решение.

Преобразуем n – член этого ряда.

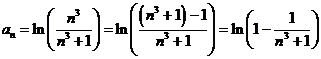
Сравним ряд 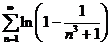 с рядом 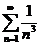, пользуясь предельным признаком сравнения:

,

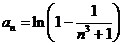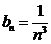
Тогда,

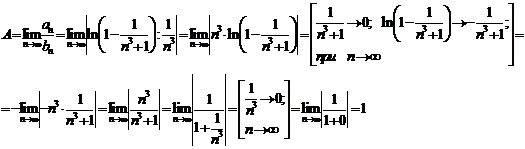
Поскольку А = 1 (0<A<+∞) – действительное число. Следовательно, ряды либо сходятся, либо расходятся. Ряд 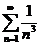 - является рядом Дирихле. Так как α = 3 > 1, то данный ряд сходится. Следовательно, и сравниваемый ряд 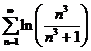 тоже сходится.

Ответ: ряд 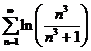 сходится.

5. Исследовать ряд на сходимость

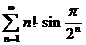
Решение.

Воспользуемся признаком Даламбера.

,

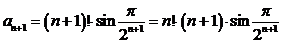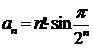
Находим m по формуле:

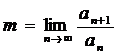
Тогда:

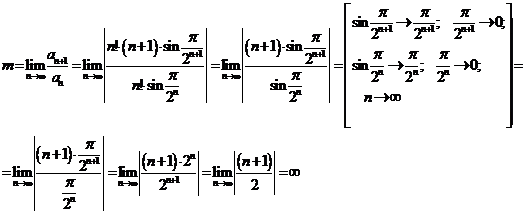
Так как 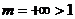, то ряд  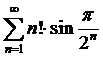расходится.

Ответ: ряд 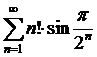 расходится.

6. Исследовать ряд на сходимость

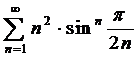
Решение.

Рассмотрим ряд

 .

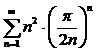Поскольку 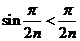 при :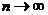

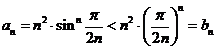
Воспользуемся признаком Даламбера.

,

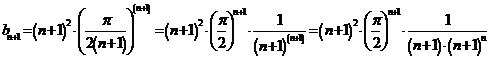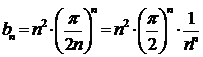
Находим m по формуле:

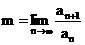
Тогда:

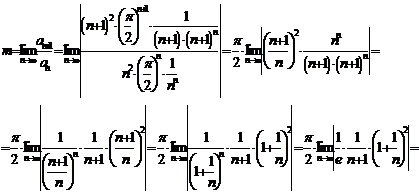
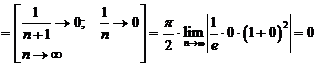
Так как 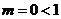, то ряд  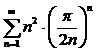сходится.

Согласно признаку сравнения сходится и ряд .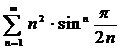

Ответ: ряд 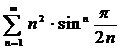 сходится.

7. Вычислить сумму ряда с точностью α..

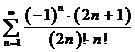 α. = 0,001.

Решение.

Прежде чем находить сумму ряда необходимо убедиться, что данный ряд сходится. Проверим исходный ряд на сходимость.

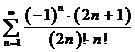 - числовой знакочередующейся.

Воспользуемся признаком Лейбница:

1)

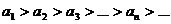
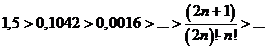
2)

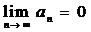
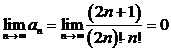
Следовательно, ряд 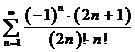 условно сходится.

Проверим абсолютную сходимость ряда 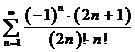. Рассмотрим ряд .

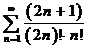Воспользуемся признаком Даламбера:

,

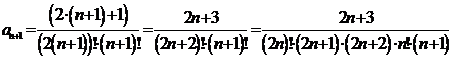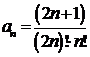
Находим m по формуле:

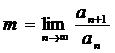
Тогда: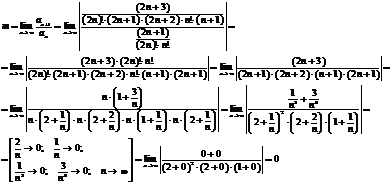

Следовательно, ряд

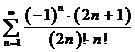  сходится абсолютно.

Вычисляем члены ряда с точностью до 4 цифр после запятой до тех пор, пока какой-нибудь член ряда по модулю не будет меньше α. = 0,001:

а₁ = -1,5 а₂ = 0,1042 а₃ = - 0,0016 а₄ = 0,0000093

Для приближённого вычисления ряда достаточно первых трех членов ряда (по следствию признака Лейбница: сумма сходящегося знакопеременного числового ряда не превышает его первого члена). Следовательно, ошибка при вычислении не превысит 0,0000093, а, значит, и 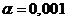. Требуемая точность достигнута.

Следовательно:

.

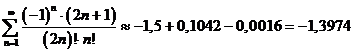Ответ: .

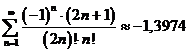8. Найти область сходимости функционального ряда

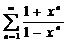
Решение.

Рассмотрим два интервала:

Проверим необходимый признак сходимости рядов: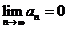

Необходимый признак не выполняется. Следовательно, при 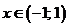 ряд 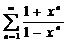 расходится.

2) 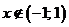, то есть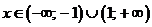

Проверим необходимый признак сходимости рядов: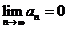

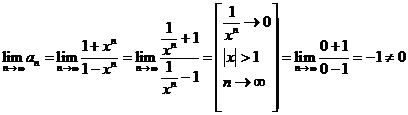
Необходимый признак не выполняется. Следовательно, при 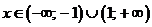 ряд 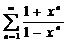 расходится.

При  имеем:

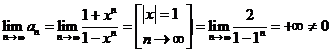
то есть ряд расходится.

Окончательно, получаем ряд расходится 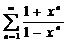 при любом Х

Ответ:

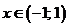
9. Найти область сходимости функционального ряда

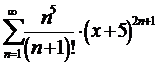
Решение.

Воспользуемся признаком Даламбера:

.

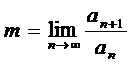В данном примере:

 ,

.

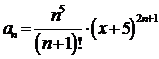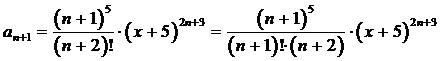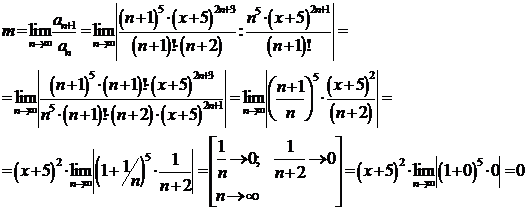
Следовательно, ряд 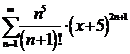 сходится при любом Х, т.е.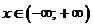

Ответ: .

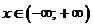10. Найти сумму ряда:

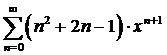
Решение.

Найдём область абсолютной сходимости ряда, пользуясь признаком Даламбера:

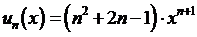
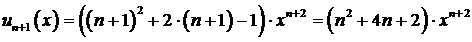
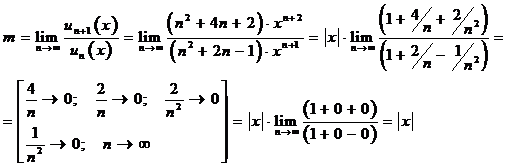
то есть 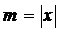. Ряд сходится для тех значений Х, для которых 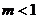, то есть , .

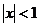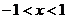При  ряд расходится, так как .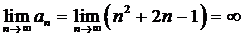

Следовательно, .

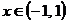Перепишем данный ряд:

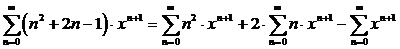
Обозначим сумму трёх рядов через 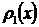,  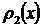и 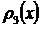 соответственно, тогда

 .

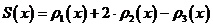Определяем область сходимости этих рядов, пользуясь признаком Даламбера:

1) :

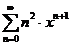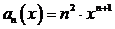
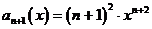
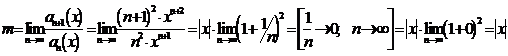
то есть 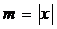. Ряд сходится для тех значений Х, для которых 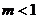, то есть , .

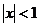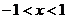Следовательно, .

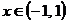2) :

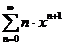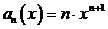
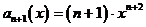
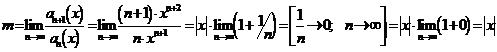
то есть 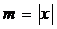. Ряд сходится для тех значений Х, для которых 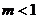, то есть , .

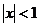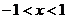Следовательно, .

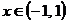3) :

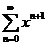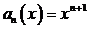
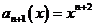
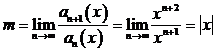
то есть 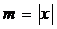. Ряд сходится для тех значений Х, для которых 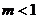, то есть , .

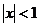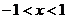Следовательно, .

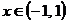Найдём сумму ряда .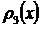

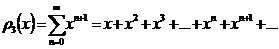
Это сумма бесконечной геометрической прогрессии: 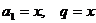, тогда:

.

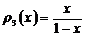Найдём сумму ряда .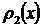

.

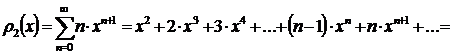
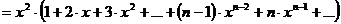Обозначим сумму ряда в скобках за 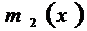 и проинтегрируем:

.

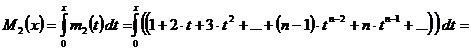
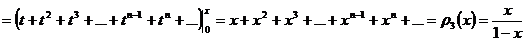Продифференцируем :

.

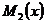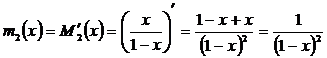Отсюда:

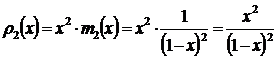
сумму ряда .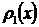

.

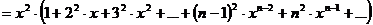Обозначим сумму ряд в скобках за 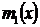 и проинтегрируем:

.

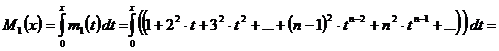
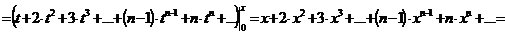
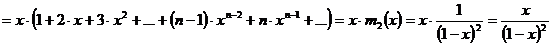Тогда, продифференцируем :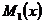

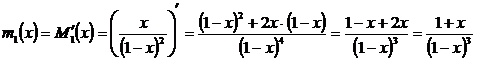
Отсюда:

.

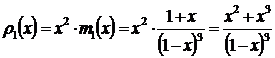Следовательно:

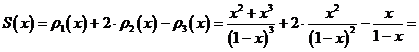
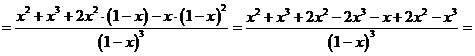
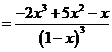 для всех .

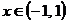Ответ: 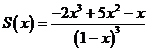 для всех .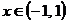