|
![[ Формула 03 ]](/wimg/9/457357.files/image004.gif)
|
— математическое ожидание;
|
|
![[ Формула 04 ]](/wimg/9/457357.files/image005.gif)
|
— дисперсия;
|
|
![[ Формула 05 ]](/wimg/9/457357.files/image006.gif)
|
— среднеквадратичное
отклонение.
|
|
Необязательным является требование воспроизводимости
последовательности. Если ГСЧ позволяет воспроизвести заново однажды
сформированную последовательность, отладка программ с использованием такого ГСЧ
значительно упрощается.
Поскольку псевдослучайные числа не являются действительно
случайными, качество ГСЧ очень часто оценивается по «случайности» получаемых
чисел. В эту оценку могут входить различные показатели, например, длина цикла (количество
итераций, после которого ГСЧ зацикливается), взаимозависимости между соседними
числами (могут выявляться с помощью различных методов теории вероятностей и
математической статистики) и т.п.
За эталон генератора случайных чисел (ГСЧ) принят такой
генератор, который порождает последовательность случайных чисел с равномерным
законом распределения в интервале (0; 1). За одно обращение данный генератор
возвращает одно случайное число.
Если наблюдать такой ГСЧ достаточно длительное время, то
окажется, что, например, в каждый из десяти интервалов (0; 0.1), (0.1; 0.2),
(0.2; 0.3), …, (0.9; 1) попадет практически одинаковое количество случайных
чисел — то есть они будут распределены равномерно по всему интервалу (0; 1).
Если изобразить на графике k = 10 интервалов и частоты Ni
попаданий в них, то получится экспериментальная кривая плотности распределения
случайных чисел.
Равномерный закон распределения
Непрерывная случайная величина Х имеет равномерный закон
распределения на отрезке [a, b], если ее плотность распределения f(x) постоянна
на этом отрезке и равна нулю вне его, т.е.
f(x)=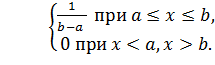
Кривая распределения f(x) и график функции распределения
F(x) случайной величины X приведены рис. 1.1.
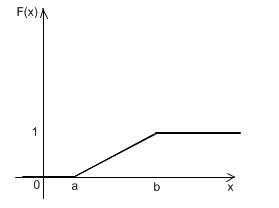
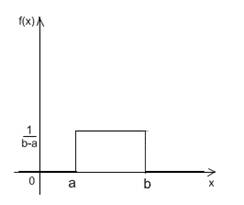
а б
рис. 1.1
Теорема. Функция распределения случайной величины Х,
распределенной по равномерному закону, есть
F(x)=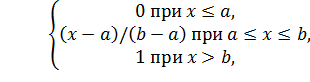
ее математическое ожидание
M(X) = (1.3)
(1.3)
а дисперсия
D(X) =  (1.4)
(1.4)
Равномерный закон распределения используется при анализе
ошибок округления при проведении числовых расчетов, в ряде задач массового
обслуживания, при статистическом моделировании наблюдений, подчиненных
заданному распределению. Так, случайная величина Х, распределенная по
равномерному закону на отрезке [0,1], называемая «случайным числом от 0 до 1»,
служит материалом для получения случайных величин с любым законом
распределения.
Понятие о критериях согласия
Полного совпадения между теоретическими и эмпирическими
частотами нет. Более того, иногда между опытными и теоретическими частотами
наблюдаются значительные расхождения. Например, если исходить
из того, что рост мужчины имеет нормальное распределение, то из 1000 мужчин 173
должны иметь рост от 161 до 164 см. В действительности их оказалось 181. Если
предположить, что число распадающихся за 1/8 мин атомов радиоактивного вещества
следует по закону Пуассона, то из 2608 промежутков должно быть 407 таких, в
которых распадается по 2 атома. На самом деле их было 383. Разница составляет
24 промежутка и кажется значительной. Эти расхождения можно объяснить двояко:
1. Несовпадения между опытными и теоретическими частотами
несущественны, они объясняются случайностью отбора отдельных элементов или
результатов единичных наблюдений. Допущение о распределении изучаемого признака
по закону, выбранному в качестве предполагаемого теоретического, должно быть
признано не противоречащим имеющимся опытным данным, согласованным с ними.
2. Различия между теоретическими и наблюденными частотами
объяснить случайностью нельзя, опытное и теоретическое распределения
противоречат друг другу. Допущение о распределении изучаемого признака по
избранному закону необходимо признать ошибочным.
Но что позволит сделать первый или второй вывод? Эту
возможность дают критерии согласия.
Можно рассмотреть различные виды расхождений между
теоретическим и опытным распределениями. Каждый вид такого расхождения является
случайной величиной. Иногда удается установить ее закон распределения. Зная
его, можно сформулировать предложение (правило), устанавливающее когда
полученное в действительности расхождение между предполагаемым теоретическим и
опытным распределениями следует признать несущественным, случайным, а когда
существенным, неслучайным. Это предложение и будет критерием согласия.
Итак, предположим, что неизвестен закон распределения
случайной величины Х, которая характеризует некоторый вид или функцию
расхождений между предполагаемым теоретическим и опытным распределениями. С
другой стороны, имея опытное распределение признака, можно найти значение α,
которое в рассматриваемом случае приняла случайная величина Х.
Закон распределения случайной величины Х определяет
вероятность того, что она примет какое-нибудь значение, не меньшее α.
Пусть эта вероятность Р(Х≥α)=β. Согласно принципу практической
уверенности при однократном наблюдении происходит немаловероятное событие.
Поэтому если величина α была получена как результат наблюдения именно
случайной величины Х, т.е. при распределении рассматриваемого признака по
предполагаемому теоретическому закону, то вероятность β не должна быть
малой. Если же вероятность β оказалась весьма малой, то это означает, что
наступило маловероятное событие, которое в соответствии с тем же принципом
практической уверенности при распределении признака в генеральной совокупности
по предложенному закону не должно было наступить. Наступление события с такой
вероятностью объясняется, по-видимому, тем, что наблюдалась случайная величина,
распределенная не по предположенному закону, а по какому-то другому. Таким
образом, в случае, когда вероятность β не мала, расхождения между
эмпирическим и теоретическим распределениями следует признать несущественными,
случайными, а опытное и теоретическое распределения – не противоречащими,
согласующимися друг с другом. Если же вероятность β мала, то расхождения
между опытным и теоретическим распределениями существенны, объяснить их
случайностью нельзя, а гипотезу о распределении признака по предложенному
теоретическому закону следует считать не подтвердившейся, она не согласуется с
опытными данными. По-видимому, при выборе предполагаемого теоретического закона
не были в достаточной степени учтены особенности имеющихся опытных данных или
при этом сказались субъективные качества исследователя. Следует внимательнее
изучить опытные данные и попытаться найти новый теоретический закон в качестве
предполагаемого для рассматриваемого признака, который лучше, полнее учитывал
бы особенности опытного распределения.
Необходимо только установить, какие вероятности считаются
«малыми». Обычно это вероятности, не превосходящие 0,01. В других случаях
считают малыми вероятности, не превосходящие 0,05.
Существует много критериев согласия. Рассмотрим критерий χ-квадрат
(Пирсона) и критерий Колмогорова.
Критерий согласия  (Пирсона)
(Пирсона)
Пусть в результате n наблюдений получен вариационный ряд
с опытными частотами n1, n2, …, nm. Тогда сумма их n1+n2+..+nm=n. Анализ
опытных данных привел, допустим, к выбору некоторого теоретического закона
распределения в качестве предполагаемого для рассматриваемого признака, а по
опытным данным найдены его параметры (если они не были известны заранее). С
помощью самого закона вычислены теоретические частоты n01, n02, …,n0m,
соответствующие эмпирическим частотам. Сумма теоретических частот также равна
объему совокупности n:
n01+ n02+…+n0m=n.
В качестве меры расхождения теоретического и
эмпирического рядов частот можно взять величину
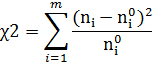
Из этого выражения видно, что χ2 равно нулю лишь при
совпадении всех соответствующих эмпирических и теоретических частот: ni =n0i (i
= 1, 2, …, m). В противном случае χ2 отлично от нуля и тем больше, чем
больше расхождения между указанными частотами.
Величина χ2 , определяемая равенством, является
случайной, которая как можно показать, имеет χ2-распределение, где k – число
степеней свободы. Число k = m – s, где m – число групп эмпирического
распределения, а s – число параметров теоретического закона, найденных с
помощью этого распределения, вместе с числом дополнительных соотношений,
которым подчинены эмпирические частоты. Если же эмпирическое распределение не
использовалось для нахождения параметров теоретического закона и теоретических
частот, а эмпирические частоты не связаны никакими дополнительными
соотношениями, то k равно числу групп эмпирического распределения, причем в
обоих случаях наблюденные частоты должны быть не малы. Малые частоты следует
объединить с соседними с тем, чтобы укрупнить группы. Это будет показано на
приводимом ниже примере.
Таким образом, схема расчета критерия согласия χ2 следующая:
По опытным данным выбрать в качестве предполагаемого
закон распределения изучаемого признака и найти его параметры.
Определить теоретические частоты с помощью полученного
закона распределения. Если среди опытных частот имеются малочисленные,
объединить их с соседними.
По формуле (1) вычислить величину χ2. Пусть она
оказалась равной χ20.
Определить число степеней свободы k.
В приложении 4 по полученным значениям χ2 и k найти
вероятность β того, что случайная величина, имеющая χ2-распределение,
примет какое-нибудь значение, не меньшее χ20 : P(χ2 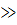 χ20) =
χ20) =  .
.
Критерий Колмогорова
На практике кроме критерия χ2 часто используется
критерий Колмогорова, в котором в качестве меры расхождения между
теоретическими и эмпирическими распределениями рассматривают максимальное значение
абсолютной величины разности между эмпирической функцией распределения  и соответствующей теоретической
функцией распределения
и соответствующей теоретической
функцией распределения
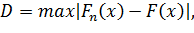
называемое статистикой критерия Колмогорова.
Доказано, что какова бы ни была функция распределения
F(x) непрерывной случайной величины X, при неограниченном увеличении числа
наблюдений (n ) вероятность неравенства P(D
) вероятность неравенства P(D ) стремится к пределу
) стремится к пределу
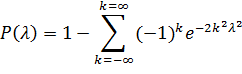
задавая уровень значимости α, из соотношения

можно найти соответствующее критическое значение  .
.
Проверка гипотезы о равномерном распределении
При использовании критерия Пирсона для проверки гипотезы
о равномерном распределении генеральной совокупности с предполагаемой
плотностью вероятности f(x) необходимо вычислив по имеющейся выборке значение,
оценить параметры a и b по формулам
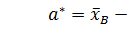 ,
, 
Где a* и b* - оценки a и b. Действительно, для
равномерного распределения
M(X) =
σ=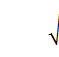 =
= ,
,
откуда можно получить систему для определения a* и b*:
f(x)=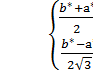 ,
,
решением которой являются выражения (*). Затем,
предполагая, что
f(x)= ,
,
можно найти теоретические частоты по формулам:
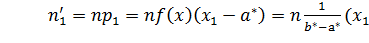 ,
,
 ,
, 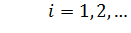 ,
,
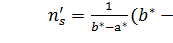 ,
,
Здесь s – число интервалов, на которые разбита выборка.
Наблюдаемое значение критерия Пирсона вычисляется по формуле:
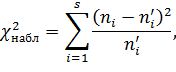
а критическое по таблице с учетом того, что число
степеней свободы k=s-3.
Для выбранного критерия строится правосторонняя
критическая область, определяемая условием
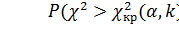 ,
,
где α – уровень значимости. Следовательно,
критическая область задается неравенством 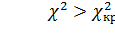 , а область принятия гипотезы –
, а область принятия гипотезы – 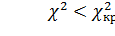 . Таким образом, если
. Таким образом, если 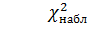 , то нулевую гипотезу принимают, если
, то нулевую гипотезу принимают, если 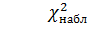 , то ее отвергают.
, то ее отвергают.
Для критерия Колмогорова теоретические и эмпирические
функции распределения находим таким же образом, как и для критерия Пирсон.
Схема применения критерия Колмогорова:
Строятся предполагаемое теоретическая функция
распределения F(x).
Находим величину  по следующей формуле
по следующей формуле
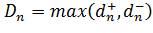
где
 ;
; 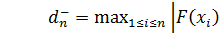
3. Если вычисленное значение
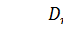 ,
,
где α критическое значение найденное при заданном
уровне значимости, то проверяемая нулевая гипотеза о том что случайная величина
Х имеет заданный закон распределения, отвергается, в противном случае гипотеза
не отвергается.
Программа вычисления  . Таблица результатов
. Таблица результатов
uses crt;
const n=100;s=10;
var
A1,h, R, min, max, x_v, D_v, at, bt,
Xi2:real;
a:array[1..N]of real;
alfa:array[1..s+1]of real;
x,mt:array[1..s]of real;
m:array[1..s]of integer;
i,k:integer;
begin
clrscr;
writeln('A1');
read(A1);
for I:=1 to n do
begin
a[i]:=sqr(a1)/1000000;
a[i]:=(trunc((a[i]-trunc(a[i]))*10000));
if a[i]<100 then
A1:=random(7999)+2000
else a1:=a[i];
a[i]:=a[i]/10000;
writeln(a[i]:8:4);
end;
begin
min:=a[1];
max:=a[1];
for i:=1 to N do
if max<a[i] then max:=a[i];
for i:=1 to N do
if min>a[i] then min:=a[i];
R:=max-min;
alfa[1]:=min;
for k:=2 to S+1 do
alfa[k]:=alfa[k-1]+h;
for k:=1 to s do
x[k]:=alfa[k]+h/2;
for k:=1 to s do
for i:=1 to N do
if
(a[i]>=alfa[k])and(a[i]<alfa[k+1]) then
m[k]:=m[k]+1;
x_v:=0; D_v:=0;
for k:=1 to s do
x_v:=x_v+x[k]*m[k];
x_v:=x_v/n; writeln(' X_v=',x_v:8:4);
for k:=1 to s do
D_v:=D_v+sqr(x[k])*m[k];
D_v:=sqrt(D_v/N-sqr(x_v)); writeln('
D_v=',D_v:8:4);
at:=x_v-D_v*sqrt(3);
bt:=x_v+D_v*sqrt(3);
mt[1]:=N*(alfa[2]-at)/(bt-at);
for k:=2 to s-1 do
mt[k]:=N*(alfa[k+1]-alfa[k])/(bt-at);
mt[s]:=N*(bt-alfa[s])/(bt-at);
Xi2:=0;
for k:=1 to s do
if mt[k]<>0 then
Xi2:=Xi2+(sqr(m[k]-mt[k]))/mt[k];
for k:=1 to s do
writeln('i',k,' x[k]=',x[k]:8:4,'
n[k]=', m[k], 'nt[k]=', mt[k]:8:4);
writeln('Xi2=',Xi2:8:4); readkey;
end; end;
end.
Таблица результатов N = 1000, m = 10, k = 7; A1=9887
|
xi
|
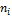
|
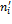
|
|
0.05
|
112
|
103.87
|
|
0.15
|
91
|
100.92
|
|
0.25
|
103
|
100.12
|
|
0.35
|
94
|
100.92
|
|
0.45
|
113
|
100.89
|
|
0.55
|
99
|
100.92
|
|
0.65
|
98
|
100.72
|
|
0.75
|
95
|
109.42
|
|
0.85
|
107
|
109.42
|
|
0.95
|
88
|
958.76
|

По таблице хи-квадрат распределения  =9.037. Так как
=9.037. Так как 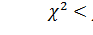 , то гипотеза H0 согласуется с опытными
данными.
, то гипотеза H0 согласуется с опытными
данными.
Программа вычисления  . Таблица результатов
. Таблица результатов
uses crt;
const n=100;
a,D,D1,b:array[1..N]of real;
i,k,j:integer;
procedure swap(var x,y:real);
var t:real;
begin
t:=x; x:=y; y:=t;
end;
function f(s:real):real;
begin
if s<=0 then
f:=0;
if (s>0) and(s<=1) then
f:=s;
if s>1 then
f:=1; end;
begin
clrscr;
writeln('A1'); read(A1);
for I:=1 to n do
begin
a[i]:=sqr(a1)/1000000;
a[i]:=(trunc((a[i]-trunc(a[i]))*10000));
if a[i]<100 then
A1:=random(7999)+2000
else a1:=a[i];
a[i]:=a[i]/10000;
end;
begin
for j:=1 to n-1 do
for i:=n downto j do
if a[i-1]>a[i] then
swap(a[i-1],a[i]);
for i:=1 to n do
end;
begin
for i:=1 to n do
D[i]:=abs(i/n-f(a[i]));
for i:=1 to n do
begin
max:=d[1];
min:=d[1];
for i:=1 to N do
if max<d[i] then max:=d[i];
for i:=1 to N do
if min>d[i] then min:=d[i];
begin
for i:=1 to n do
D1[i]:=abs(f(a[i])-(i-1)/n);
for i:=1 to n do
begin
max1:=d1[1];
min1:=d1[1];
for i:=1 to N do
if max1<d1[i] then max1:=d1[i];
for i:=1 to N do
if min1>d1[i] then min1:=d1[i];
writeln('max',max:8:4)
writeln('max1',max1:8:4);
alf:=sqrt(n)*max;
writeln('alf',alf:8:3);
readkey;
end;
end.
Таблица результатов
N = 100 ; A1=9876

При уровне значимости 0,1 критическое значение равняется
1,22.
По формуле 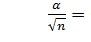 подставляя это значение получим
подставляя это значение получим 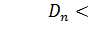 следовательно гипотеза о равномерном
распределении случайных чисел полученных методом Неймана неотвергается .
следовательно гипотеза о равномерном
распределении случайных чисел полученных методом Неймана неотвергается .
Заключение
Установленный теоретический закон отличается
незначительно от закона, полученного в результате эксперимента. Эти расхождения
объясняются случайными обстоятельствами, связанными с ограниченным числом
наблюдений.
Критерий Пирсона опровергает гипотезу о том, что
псевдослучайные числа полученные методом Неймана не распределены по
равномерному закону распределения с уровнем значимости α=0.25.
Числовые характеристики близки к статистическим
параметрам, характерных для равномерно распределенных чисел
Следовательно, случайные числа получаемые методом Неймана
распределены равномерно на интервале (0,1).
Список литературы
1.
Гмурман В. Е. - Теория вероятностей и математическая статистика.- М.: Высш. шк.,
2003
2.
Кремер Н. Ш. – Теория вероятностей и математическая статистика.- М.: Юнити,
2006
3.
Крамер Г. – Математические методы статистики. – М.: Мир, 1975
4.
Гнеденко Б. В. – Теория вероятностей и математическая статистика.- М.: Наука, 1970
5. Ветцель
Е.С.; Овчаров Л.А. - Теория вероятностей. - М.:Наука,1986
6. Ермаков
С.М.; Михайлов Г.А.- Статистическое моделирование. - М.: Наука, 1983