Фактор-группы. Cмежные классы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ
БЕЛАРУСЬ
Учреждение образования
Математический факультет
Кафедра алгебры и методики
преподавания математики
Курсовая работа
СОДЕРЖАНИЕ
Ведение
1.Основные определения и теоремы
2.Смежные классы
2.1. Правые и левые смежные классы
2.2 Двойные смежные классы
3. Нормальные подгруппы и фактор-группы
3.1 Нормальные подгруппы
3.2 Фактор-группы
Заключение
Список использованных источников
ВВЕДЕНИЕ
Первый значительный
вклад в теорию групп внес Эварист Галуа (1811–1832) при исследовании вопроса о
разрешимости в радикалах алгебраических уравнений. Именно Галуа впервые ввел
понятие группы и попытался выяснить, как они устроены. До него группы в виде
подстановок корней уравнения возникли также в работах Лагранжа (1771), Роффини
(1799) и Абеля (1825).
В 1830–1832 годах
Галуа пришел к понятиям нормальной подгруппы, разрешимой группы, простой группы.
С тех пор многие ученые математики занимались исследованиями в вопросах
связанными с группами, вводили новые понятия, строили свои догадки,
формулировали и доказывали теоремы.
Теория групп – один из
центральных разделов современной алгебры, в настоящее время активно
разрабатываемый в Беларуси в научных школах Минска, Гомеля, Витебска,
Новополоцка, Мозыря.
Понятие группы приобретает в настоящее время все
большее господство над самыми различными разделами математики и ее приложений и
наряду с понятием функции относится к самым фундаментальным понятиям всей
математики.
Понятие группы не труднее понятия функции; его можно
освоить на самых первых ступенях математического образования, тем более что сделать
это можно на материале элементарной математики. Вместе с тем знакомство с этой
теорией кажется одним из самых естественных способов ознакомления с современной
математикой вообще.
Моя цель состоит в том, чтобы разобраться с
начальными понятиями, связанными с группами: фактор-группы, смежные классы,
доказать наиболее важные теоремы, следствия, выделить некоторые свойства.
1.ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ТЕОРЕМЫ
Рассмотрим некоторое непустое множество G, на котором
определена бинарная алгебраическая операция.
ОПРЕДЕЛЕНИЕ 1.1. Пара (G,*) называется группой, если:
1) операция ассоциативна, т.е. для любых a, b, c ÎG выполняется
a*(b*c)=(a*b)*c;
2) в G существует нейтральный элемент относительно, т.е.
для любого a Î G
найдется такой элемент e ,что выполняется
a*e=e*a=a
3) для любого элемента G существует симметричный
элемент относительно, т.е. для любых a, bÎ G выполняется
a*b=b*a=e;
ОПРЕДЕЛЕНИЕ 1.2. Подмножество H группы G называется
подгруппой, если H-группа относительно той же операции, которая определена на G.
ОПРЕДЕЛЕНИЕ 1.3. Зафиксируем в группе G элемент a.
Пересечение всех подгрупп группы G, содержащих элемент а, называется циклической
подгруппой, порожденной элементом а, и обозначается áаñ.
ОПРЕДЕЛЕНИЕ 1.4. Если G совпадает с одной из своих
циклических подгрупп, то G называют циклической группой.
ТЕОРЕМА 1.1. Пусть элемент аÎG имеет конечный порядок k.
Тогда
áаñ ={e,
a, a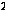 , … , a
, … , a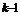 }
}
Кроме того, а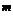 = e в точности тогда, когда k делит m.
= e в точности тогда, когда k делит m.
ТЕОРЕМА 1.2. Все подгруппы бесконечной циклической
группы G = áаñ исчерпываются
единичной подгруппой E={e} и бесконечными подгруппами á а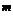 ñ
для каждого натурального m.
ñ
для каждого натурального m.
ТЕОРЕМА 1.3.Все подгруппы конечной циклической группы
áаñ порядка n
исчерпываются циклическими подгруппами á а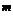 ñ
порядка n/m для каждого натурального m, делящего n.
ñ
порядка n/m для каждого натурального m, делящего n.
ТЕОРЕМА 1.4. Непустое подмножество H
группы G будет подгруппой тогда и только тогда, когда h h
h
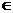 H и h
H и h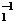
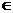 H.
H.
2. СМЕЖНЫЕ КЛАССЫ
2.1 Правые и левые смежные классы
Пусть G – группа, H – ее подгруппа и gÎG.
ОПРЕДЕЛЕНИЕ 2.1.1. Правым смежным
классом группы G по подгруппе H называется множество Hg= {hg | hÎH}
всех элементов группы G вида hg
, где h “пробегает” все элементы подгруппы H.
Аналогично определяется левый смежный класс gH={gh | hÎH}.
ЛЕММА 2.1.1. Пусть G – группа, H
– подгруппа. Тогда справедливы утверждения:
1) H=He;
2) gÎHg для каждого gÎG;
3) если a Î H, то Ha=H; если bÎ Ha , то Hb=Ha;
4) Ha=Hb тогда и только
тогда, когда ab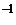 ÎH;
ÎH;
5) два смежных класса либо совпадают, либо их пересечение пусто;
6) если H – конечная
подгруппа, то | Hg | = | H | для всех gÎG.
Доказательство
Первые три свойства вытекают из определения правого смежного класса
(4) Если Ha = Hb, то ea = hb, hÎH
и ab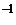 = hÎH. Обратно, если ab
= hÎH. Обратно, если ab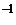 ÎH, то aÎHb и Ha=Hb по
утверждению 3.
ÎH, то aÎHb и Ha=Hb по
утверждению 3.
(5) Пусть Ha Ç Hb ≠Æ и c Î Ha Ç Hb. Тогда c=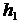 a=
a=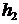 b и ab
b и ab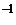 =
=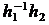 ÎH. Теперь Ha=Hb по утверждению 4).
ÎH. Теперь Ha=Hb по утверждению 4).
(6) Для каждого gÎG
отображение φ: h→hg есть биекция множеств H и Hg. Поэтому | H |
= | Hg |
Ч.т.д.
Из свойств 2) и 5) следует, что каждый элемент группы G
содержится точно в одном правом смежном классе по подгруппе H.
Это свойство позволяет ввести следующее определение.
ОПРЕДЕЛЕНИЕ 2.1.2. Пусть H подгруппа группы G. Подмножество T элементов группы G называется
правой трансверсалью подгруппы H в группе G , если T содержит точно один
элемент из каждого правого смежного класса группы G по
подгруппе H .Итак, если T = {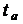 | aÎI} –правая трансверсаль подгруппы H в
группе G, то G
=
| aÎI} –правая трансверсаль подгруппы H в
группе G, то G
= 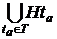 , H
, H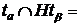 Æ при
Æ при 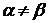 .
.
Таким образом, справедлива теорема.
ТЕОРЕМА 2.1.1. Если H – подгруппа группы G, то G является подгруппой
непересекающихся правых смежных классов по подгруппе H.
Если G – конечная группа, то число различных
правых смежных классов по подгруппе H также будет
конечно, оно называется индексом подгруппы H в группе G и обозначается через |G : H|. Ясно, что индекс подгруппы H в
конечной группе G совпадает с числом элементов в правой
трансверсали T подгруппы H,
т.е.
|G : H|=|T|=|G|/|H|
ТЕОРЕМА 2.1.2. (Лагранжа) Если H-подгруппа конечной группы G, то | G | = | H || G : H |. В частности, порядок конечной
группы делится на порядок каждой своей подгруппы.
Доказательство.
Пусть индекс H в группе G равен n . По теореме 2.1.1. имеем
разложение
G=Hg
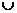 Hg
Hg
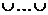 Hg
Hg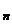 , Hg
, Hg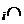 Hg
Hg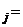 Æ при i ≠ j.
Æ при i ≠ j.
| Hg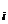 | = |H| для всех i, то | G
| = | H || G : H |
| = |H| для всех i, то | G
| = | H || G : H |
СЛЕДСТВИЕ 2.1.1. Порядок каждого элемента конечной группы делит порядок
всей группы.
Доказательство
Порядок элемента a совпадает с порядком
циклической подгруппы áаñ, порожденный этим
элементом, см. теорему 1.1. Поэтому, | á аñ | = | a | делит | G |.
Аналогично определяется левая трансверсаль подгруппы H
в группе G. Если L={ l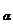 | aÎ J } – левая
трансверсаль подгруппы H в группе G,
то
| aÎ J } – левая
трансверсаль подгруппы H в группе G,
то
G=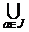 l
l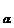 H,
l
H,
l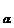 H Ç l
H Ç l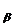 H=Æ при
H=Æ при 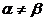 .
.
Ясно, что индекс подгруппы H в конечной группе G совпадает с числом элементов в левой трансверсали L подгруппы H, т.е. | G : H |=| L
|. Для левой трансверсали справедлив аналог теоремы 2.1.1 .Поэтому из теоремы
Лагранжа имеем
СЛЕДСТВИЕ 2.1.2. Число левых и число правых смежных классов конечной
группы G по подгруппе H совпадают.
ТЕОРЕМА 2.1.3. В группе простого порядка
нет неотрицательных подгрупп. В частности, группа простого порядка циклическая.
Доказательство.
Пусть G – конечная группа простого порядка p. Если H – подгруппа группы G, то по теореме Лагранжа | H | делит
| G |. Поэтому либо | H |=1 и H – единичная подгруппа, либо | H |= p и H совпадает с группой G. Выберем неединичный элемент а в группе G
и рассмотрим циклическую подгруппу áаñ,
порожденную этим элементом. Так как a ≠
e ,то á
аñ ≠ E, поэтому áаñ = G
и G – циклическая группа.
ТЕОРЕМА 2.1.4. Пусть H ≤ K ≤
G и G – конечная группа. Если T – правая трансверсаль подгруппы H в
группе K, а S – правая
трансверсаль подгруппы K в группе G,
то TS – правая трансверсаль подгруппы H
в группе G. В частности, | G : H | = | G : K
|| K : H |.
Доказательство
Пусть
T={t , … ,t
, … ,t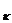 }, S={s
}, S={s , … , s
, … , s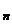 }
}
Тогда
K=Ht
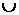 . . .
. . . 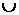 Ht
Ht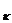 , Ht
, Ht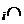 Ht
Ht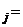 Æ, i ≠j;
Æ, i ≠j;
G=Ks
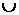 . . .
. . . 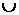 Ks
Ks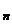 , Ks
, Ks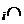 Ks
Ks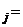 Æ, i ≠j.
Æ, i ≠j.
Теперь
G =( Ht
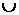 . . .
. . . 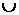 Ht
Ht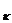 )s
)s
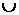 . . .
. . . 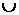 (
Ht
(
Ht
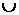 . . .
. . . 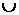 Ht
Ht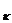 )s
)s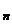 . (2.1.1)
. (2.1.1)
Предположим, что Ht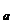 s
s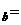 Ht
Ht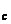 s
s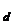 для некоторых натуральных a,b,c и d. Тогда
для некоторых натуральных a,b,c и d. Тогда
t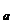 s
s (t
(t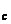 s
s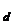 )
) = t
= t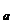 s
s s
s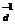 t
t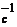 ÎH ≤ K,
ÎH ≤ K,
поэтому
s s
s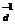 Î t
Î t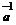 Kt
Kt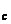 = K,
K s
= K,
K s =Ks
=Ks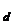
Но s и s
и s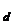 – элементы из правой трансверсали
подгруппы K в группе G, поэтому
s
– элементы из правой трансверсали
подгруппы K в группе G, поэтому
s = s
= s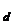 и b = d. Теперь
и b = d. Теперь
t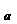 s
s (t
(t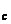 s
s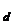 )
)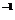 = t
= t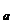 t
t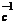 ÎH, H t
ÎH, H t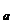 =Ht
=Ht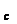
и a = c.
Таким образом, формула (2.1.1.) является разложением группы G
по подгруппе H и TS – правая
трансверсаль подгруппы H в группе G.
Так как индекс подгруппы совпадает с числом элементов в правой трансверсали
этой подгруппы, то
|G : H
|=| TS |=| T | | S |=| K : H
|| G : K |
Отметим, что теорема Лагранжа вытекает из теоремы
2.1.4. при H=E.
2.3. Двойные смежные
классы
Пусть H и K – подгруппы группы G и g Î G. Множество
HgK ={
hgk | h Î H, k Î K}
называется двойным смежным классом группы G по подгруппам H и K
ЛЕММА 2.3.1. Пусть H и K –подгруппы группы G. Тогда
справедливы следующие утверждения:
1) Каждый элемент gÎ G содержится в единственном двойном
смежном классе HgK;
2) Два двойных смежных класса по H
и K либо совпадают, либо их пересечение пусто;
3) Группа G есть объединение
непересекающихся двойных смежных классов по подгруппам H
и K;
4) Каждый двойной смежный класс по H
и K есть объединение правых смежных классов по H и левых смежных классов по K;
5) Если группа G конечна, то
двойной смежный класс HgK содержит
| K: H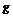
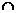 K | правых смежных классов по H и | H : H
K | правых смежных классов по H и | H : H 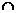 K
K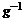 |
левых смежных классов по К.
|
левых смежных классов по К.
Доказательство.
(1)Так как каждая
подгруппа содержит единичный элемент, то
g=ege Î HgK
Допустим, что gÎHxK. Тогда g=hxk
для некоторых hÎH, kÎK и
HgK=H(hxk)K=HxK.
(2) и (3) следуют из (1)
(4)Так как
HgK=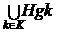 =
=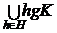 ,
,
то утверждение (4)
доказано.
Подсчитаем число
правых смежных классов в разложении HgK=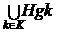 по
подгруппе H. Допустим, что Hgk
по
подгруппе H. Допустим, что Hgk =Hgk
=Hgk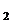 . Тогда
. Тогда
Hg k k
k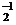 = Hg и k
= Hg и k k
k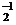 Î g
Î g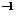 Hg
Hg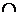 K=H
K=H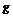
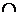 K
K
Справедливо и обратное, т.е. если k k
k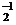 Î H
Î H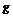
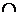 K, то
K, то
k k
k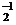 Î g
Î g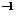 Hg,
g k
Hg,
g k k
k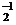 ÎHg, g k
ÎHg, g k ÎHgk
ÎHgk
и Hg k = Hgk
= Hgk . Поэтому, в двойном смежном классе HgK правых смежных классов по H
столько, сколько их в группе K по
подгруппе H
. Поэтому, в двойном смежном классе HgK правых смежных классов по H
столько, сколько их в группе K по
подгруппе H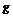
 K.
K.
Аналогично,
Hgk=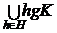 и h
и h gK=h
gK=h gK
gK
тогда и только тогда,
когда h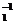 h
h ÎH
ÎH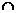 K
K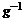 . Поэтому, в произведении HgK левых смежных классов по K будет
точно столько, каков индекс
. Поэтому, в произведении HgK левых смежных классов по K будет
точно столько, каков индекс
|H : H 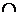
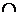 K
K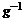 |
|
Произведение подгрупп.
При g = e
двойной смежный класс HgK=HK={hk | hÎH , kÎK} превращается в произведение подгрупп H и K . В
общем случае HK не является подгруппой.
Пример:
Найдем разложение
симметрической группы S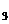 в
левые смежные классы по подгруппе
в
левые смежные классы по подгруппе 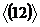 .
.
Для этого найдем все
левые смежные классы группы
S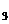 ={Î,(12),(13),(23),(123),(132)}
по подгруппе H=
={Î,(12),(13),(23),(123),(132)}
по подгруппе H=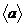 ={Î,(12)}
={Î,(12)}
ÎH = Î{Î, (12)} =
{Î, (12)}
= H,
(12)H =
(12) {Î,
(12)} = {(12), Î}
= H,
(13)H =
(13) {Î,
(12)} = {(13), (123)},
(23)H =
(23) {Î,
(12)} = {(23), (132)},
(123)H =
(123){Î,(12)}
= {(123),(13)} = (13)H,
Искомое разложение принимает вид
S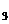 =ÎH
=ÎH 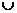 (13)
H
(13)
H 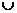 (23) H.
(23) H.
3. НОРМАЛЬНЫЕ
ПОДГРУППЫ И ФАКТОР-ГРУППЫ
3.1 Нормальные
подгруппы
Подгруппа H
называется нормальной подгруппой группы G, если xH=Hx
для всех xÎG. Запись H 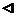 G читается так:
“H – нормальная
подгруппа группы G”. Равенство xH=Hx означает, что
для любого элемента h
G читается так:
“H – нормальная
подгруппа группы G”. Равенство xH=Hx означает, что
для любого элемента h ÎH
существует элемент h
ÎH
существует элемент h Î H такой, что xh
Î H такой, что xh = h
= h x.
x.
ТЕОРЕМА 3.1.1.(Критерий
нормальной подгруппы) Для подгруппы H группы G следующие
утверждения эквивалентны:
1) H –
нормальная подгруппа группы G;
2) Подгруппа H
вместе с каждым своим элементом содержит все ему сопряженные элементы, т.е. h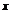 ÎH для всех hÎH и всех xÎG;
ÎH для всех hÎH и всех xÎG;
3) Подгруппа H совпадает с
каждой своей сопряженной подгруппой, т.е. H=H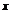 для всех xÎG.
для всех xÎG.
Доказательство.
Доказательство проведем по схеме (1)  (2)
(2)  (3)
(3) (4)
(4)
(1)
 (2). Пусть H
(2). Пусть H
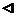 G,
т.е. xH=Hx
для всех xÎG.
Если h — произвольный элемент из H, то hx
G,
т.е. xH=Hx
для всех xÎG.
Если h — произвольный элемент из H, то hx 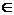 Hx =
xH. Поэтому существует элемент h
Hx =
xH. Поэтому существует элемент h
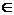 H такой, что hx = x h
H такой, что hx = x h .Теперь x
.Теперь x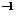 hx =
h
hx =
h
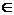 H.
H.
(2)
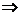 (3). Пусть выполняются требование 2).
Тогда H
(3). Пусть выполняются требование 2).
Тогда H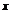 = {h
= {h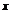 | h
| h 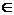 H} Í Í
H для всех x
H} Í Í
H для всех x 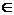 G. В частности, Hx
G. В частности, Hx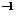 Í H, т.е. xHx
Í H, т.е. xHx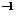 Í H. Теперь
Í H. Теперь
H
Í
x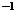 Hx =H
Hx =H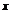 и H
= H
и H
= H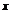 для всех x
для всех x 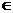 G.
G.
(3)
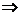 (1). Если H
(1). Если H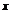 = H
для всех x
= H
для всех x 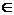 G, то x
G, то x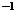 Hx =
H и Hx = xH для всех x
Hx =
H и Hx = xH для всех x 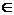 G, т.е. H – нормальная подгруппа
группы G.
G, т.е. H – нормальная подгруппа
группы G.
Ч.т.д.
СЛЕДСТВИЕ
3.1.1.
Если
H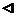 G и h
G и h 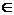 H, то h
H, то h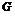 Í
H. Обратно, если h
Í
H. Обратно, если h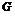 Í
H для всех h
Í
H для всех h 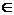 H, то H
H, то H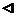 G.
G.
Понятие
"нормальная подгруппа" можно рассматривать не только по отношению ко
всей группе, но и относительно подгрупп. Если H £
K £
G, то подгруппа H будет нормальной в K, если xH = Hx для всех x 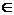 K.
K.
Простая
группа. В каждой группе G тривиальные подгруппы (единичная подгруппа E и сама
группа G) являются нормальными подгруппами. Если в неединичной группе G нет
других нормальных подгрупп, то группа G называется простой. Единичную группу E
считают непростой группой.
ТЕОРЕМА
3.1.2. Абелева простая группа является циклической группой простого порядка.
Обратно, каждая группа простого порядка будет простой абелевой группой.
3.2
Фактор-группы
Пусть
H — нормальная подгруппа группы G. Обозначим через 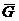 совокупность
всех левых смежных классов группы G по подгруппе H, т.е.
совокупность
всех левых смежных классов группы G по подгруппе H, т.е. 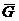 = ={xH | x Î
G}. Положим
= ={xH | x Î
G}. Положим
(xH)(yH)
= xyH. (3.2.1)
Проверим,
что это равенство задает алгебраическую операцию на множестве 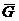 . Если xH = x
. Если xH = x H, yH
= y
H, yH
= y H для некоторых x
H для некоторых x ,
y
,
y Î G, то x
Î G, то x = xh, y
= xh, y = =yg,
h и g Î
H. Поэтому
= =yg,
h и g Î
H. Поэтому
(x H)(y
H)(y H) = x
H) = x y
y H =
(xh)(yg)H = xy(y
H =
(xh)(yg)H = xy(y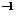 hy)gH = xyH,
hy)gH = xyH,
т.к.
y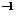 hy ÎH по теореме 3.1.1.
Таким образом, равенство (3.2.1) не зависит от выбора представителей смежных
классов и каждой паре xH, yH ставится в соответствие единственный элемент xyH.
hy ÎH по теореме 3.1.1.
Таким образом, равенство (3.2.1) не зависит от выбора представителей смежных
классов и каждой паре xH, yH ставится в соответствие единственный элемент xyH.
Ясно,
что предложенная операция (3.2.1) определена на 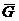 и
ассоциативна. Элемент eH = H будет единичным, а элемент a
и
ассоциативна. Элемент eH = H будет единичным, а элемент a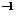 H — обратным к элементу aH. Таким
образом, доказана следующая.
H — обратным к элементу aH. Таким
образом, доказана следующая.
ТЕОРЕМА
3.2.1. Совокупность 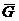 = {xH | x Î
G} всех левых смежных классов группы G по нормальной подгруппе H с операцией
= {xH | x Î
G} всех левых смежных классов группы G по нормальной подгруппе H с операцией
(xH)(yH)
= xyH
образует
группу с единичным элементом eH = H и обратным элементом (aH)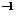 = a
= a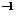 H.
H.
Группа
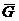 называется фактор-группой группы G по
подгруппе H и обозначается через G/H.
называется фактор-группой группы G по
подгруппе H и обозначается через G/H.
Если
H не будет нормальной подгруппой, то равенство (3.2.1.) не будет задавать
алгебраическую операцию, и совокупность левых смежных классов не будет группой.
Очевидно,
что если группа G конечна, то фактор-группа группы G по любой нормальной
подгруппе H также будет конечной группой порядка, равного индексу подгруппы H в
группе G, т.е.
|G/H
|=| G : H |=| G | / | H |
ЛЕММА
3.2.1. Если фактор-группа G/Z(G) циклическая, то группа G абелева.
Доказательство.
Пусть
G/Z(G) = á gZ(G)ñ
циклическая группа и a, b — произвольные элементы группы G. Тогдаa
= g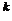 z
z , b
= g
, b
= g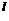 z
z , z
, z , z
, z Î
Z(G),
k, l
Î Z
Î
Z(G),
k, l
Î Z
и
ab = g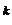 z
z g
g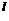 z
z =
g
=
g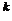 g
g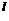 z
z z
z = g
= g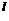 g
g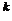 z
z z
z =
g
=
g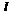 z
z g
g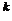 z
z = ba
= ba
ТЕОРЕМА
3.2.2. Все фактор-группы бесконечной циклической группы á
аñ
исчерпываются бесконечной циклической группой á
аñ
/ E »
á
а ñ
и конечными циклическими группами áaáа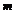 ñ ñ
порядка m для каждого натурального числа m.
ñ ñ
порядка m для каждого натурального числа m.
Доказательство.
По
теореме 1.2 все подгруппы бесконечной циклической группы A = áаñ
исчерпываются единичной подгруппой E и бесконечными циклическими подгруппами M
= á
а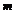 ñ, m Î
N. Так как каждая циклическая группа абелева, то в ней любая подгруппа
нормальна.
ñ, m Î
N. Так как каждая циклическая группа абелева, то в ней любая подгруппа
нормальна.
Фактор-группа
A/E очевидно будет бесконечной циклической группой, изоморфной A. Так как A =
{a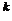 | k Î
Z}, то фактор-группа A/M состоит из смежных классов a
| k Î
Z}, то фактор-группа A/M состоит из смежных классов a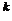 M,
k Î Z. Если два смежных класса совпадут a
M,
k Î Z. Если два смежных класса совпадут a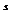 M = a
M = a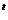 M, то
a
M, то
a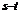 ÎM
и s - t кратно m. Отсюда следует, что смежные классы M, aM, a
ÎM
и s - t кратно m. Отсюда следует, что смежные классы M, aM, a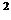 M, . , a
M, . , a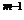 M попарно
различны. Кроме того, для любого a
M попарно
различны. Кроме того, для любого a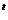 M Î
A/M имеем:
M Î
A/M имеем:
t = mq
+ r, 0 ≤ r
< m
и
a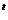 M
= a
M
= a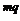 a
a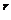 M = a
M = a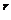 M.
M.
Таким
образом,
A/M = {M, aM, a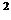 M, .
. . , a
M, .
. . , a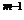 M} = áaMñ,
M} = áaMñ,
т.е.
фактор-группа A/M будет конечной циклической группой порядка m.
ТЕОРЕМА
3.2.3. Все фактор-группы конечной циклической группы áañ
порядка n исчерпываются конечными циклическими группами áaáа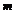 ñ ñ
порядка m для каждого натурального m, делящего n.
ñ ñ
порядка m для каждого натурального m, делящего n.
Доказательство.
По
теореме 1.3, все подгруппы конечной циклической группы A = áañ
порядка
n исчерпываются циклическими подгруппами M = á
а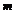 ñ порядка n/m для
каждого натурального m, делящего n. Легко проверить, что
ñ порядка n/m для
каждого натурального m, делящего n. Легко проверить, что
A/M = áaMñ
= {aM, a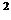 M, . . . , a
M, . . . , a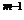 M,M},
M,M},
т.е.
A/M=áaáа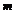 ñ ñ
будет циклической группой порядка m.
ñ ñ
будет циклической группой порядка m.
Условимся
через S(G,H) обозначать совокупность всех подгрупп группы G, содержащих
подгруппу H. В частности, S(G,E)=S(G) — совокупность всех подгрупп группы G, а
S(G,G) = {G}.
ТЕОРЕМА
3.2.4.(Теорема о соответствии)
Пусть
H — нормальная подгруппа группы G. Тогда:
1)
если U — подгруппа группы G и H ≤ U, то 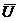 =
U/H — подгруппа фактор-группы
=
U/H — подгруппа фактор-группы 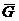 = G/H;
= G/H;
2)
каждая подгруппа фактор-группы 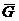 = G/H имеет вид
= G/H имеет вид 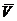 = V/H, где V— подгруппа группы G и H £V
;
= V/H, где V— подгруппа группы G и H £V
;
3)
отображение 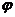 : U →
: U → 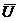 является
биекцией множества S(G,H) на множество S(
является
биекцией множества S(G,H) на множество S(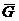 );
);
4)
если N Î
S(G,H), то N — нормальная подгруппа группы G тогда и только тогда, когда N/H –
нормальная подгруппа фактор-группы G/H.
Доказательство.
(1)
Пусть U Î
S(G,H) и пусть 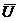 ={uH | u Î
U} — совокупность смежных классов группы U по своей нормальной подгруппе H.
Если u
={uH | u Î
U} — совокупность смежных классов группы U по своей нормальной подгруппе H.
Если u H, u
H, u H Î
Î
H Î
Î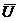 , то u
, то u , u
, u Î U, а так как U —
подгруппа, то u
Î U, а так как U —
подгруппа, то u u
u Î
U и u
Î
U и u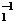 Î U. Поэтому,
Î U. Поэтому,
(u H)(u
H)(u H) = u
H) = u u
u H Î
H Î 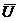 , (u
, (u H)
H)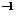 = u
= u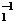 H Î
H Î
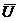
и
по критерию подгруппы (теорема 1.4) совокупность 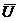 –
подгруппа группы
–
подгруппа группы 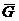 .
.
(2)
Пусть 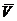 — произвольная подгруппа из
— произвольная подгруппа из 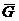 . Тогда
. Тогда 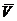 состоит
из некоторых смежных классов группы G по подгруппе H. Обозначим через V
множество всех тех элементов группы G, из которых состоят смежные классы,
принадлежащие
состоит
из некоторых смежных классов группы G по подгруппе H. Обозначим через V
множество всех тех элементов группы G, из которых состоят смежные классы,
принадлежащие 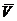 , т.е. V = {x Î
G | xH Î
, т.е. V = {x Î
G | xH Î
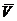 }. Если v
}. Если v , v
, v Î V, то v
Î V, то v H, v
H, v H Î
H Î
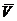 , а так как
, а так как  —
подгруппа, то
—
подгруппа, то
(v H)( v
H)( v H) =
v
H) =
v v
v H Î
H Î
 и (v
и (v H)
H) = v
= v H Î
H Î
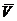
Следовательно,
v v
v Î
V и v
Î
V и v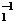 Î V , т.е. V — подгруппа
группы G. Ясно, что H ≤ Vэ
Î V , т.е. V — подгруппа
группы G. Ясно, что H ≤ Vэ
(3)
Отображение 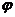 : U →
: U → 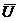 будет
сюръекцией на основании утверждения (2). Докажем, что
будет
сюръекцией на основании утверждения (2). Докажем, что 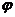 –
инъекция. Пусть U и V — подгруппы, содержащие H, и предположим, что подгруппы
–
инъекция. Пусть U и V — подгруппы, содержащие H, и предположим, что подгруппы 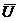 = {uH | u Î
U} и
= {uH | u Î
U} и 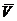 = { vH | v Î
V } совпадают. Тогда для любого элемента u Î U существует элемент v
Î
V такой, что uH = vH. Поэтому v
= { vH | v Î
V } совпадают. Тогда для любого элемента u Î U существует элемент v
Î
V такой, что uH = vH. Поэтому v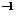 u Î
H ≤ V ∩ U. Теперь u Î V и U ≤ V .
Аналогично проверяется обратное включение. Следовательно U = V и
u Î
H ≤ V ∩ U. Теперь u Î V и U ≤ V .
Аналогично проверяется обратное включение. Следовательно U = V и 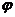 — инъекция.
— инъекция.
(4)
Если N
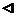 G,
N Î
S(G,H),
то
G,
N Î
S(G,H),
то
(gH)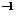 (nH)(gH) = g
(nH)(gH) = g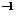 ngH Î
N/H
ngH Î
N/H
g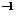 ngH = (gH)
ngH = (gH) 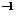 (nH)(gH) Î
(nH)(gH) Î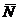
и
g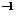 ngH
ÎN,
значит N
ngH
ÎN,
значит N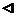 G.
G.
Пример:
Найдем все фактор-группы группы S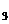 .
.
Среди
подгрупп группы S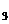 со своими сопряженными
совпадают следующие подгруппы: E,
S
со своими сопряженными
совпадают следующие подгруппы: E,
S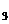 ,
H=
,
H=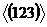 (см.
пример выше). По теореме 4.1. эти три подгруппы нормальны в S
(см.
пример выше). По теореме 4.1. эти три подгруппы нормальны в S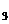 . Ясно, что S
. Ясно, что S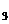 / S
/ S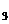 – единичная группа, а S
– единичная группа, а S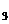 / E
изоморфна S
/ E
изоморфна S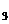 .Порядок подгруппы H=
.Порядок подгруппы H=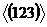 равен 3, а порядок S
равен 3, а порядок S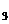 / H
равен 2. Поэтому S
/ H
равен 2. Поэтому S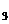 / H
– циклическая группа порядка 2.Смежные классы S
/ H
– циклическая группа порядка 2.Смежные классы S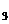 по H
исчерпываются классами H
и (12)H. Таким образом, группа
S
по H
исчерпываются классами H
и (12)H. Таким образом, группа
S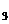 имеет
три фактор-группы: S
имеет
три фактор-группы: S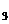 / H
/ H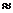 S
S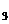 , S
, S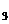 / S
/ S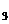
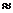 E,
S
E,
S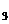 / H={H,(12)H}=
/ H={H,(12)H}=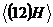 .
.
ЗАКЛЮЧЕНИЕ
Теория групп является одним из самых важных разделов математики, а
понятия фактор-группы и смежных классов – всего лишь маленькая частичка этого
огромного айсберга знаний. В мире все еще существуют нерешенные проблемы теории
групп, разбираясь же в самых простых определениях и теоремах можно прийти к
чему-то большему. Возможно, в недалеком будущем именно мне удастся разрешить
эти вопросы.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Александров,
П.С. Введение в теорию групп /П.С. Александров –М.:Наука, 1980.
2. Богопольский,
О.В. Введение в теорию групп /О.В. Богопольский – М.: Институт компьютерных
исследований, 2002.
3. Монахов, В.С.
Введение в теорию конечных групп и их классов /В.С.Монахов – Мн.:Вышэйшая
школа, 2006.