Дифференциальные уравнения с запаздывающим аргументом
1. Определения
Дифференциальные
уравнения с запаздывающим аргументом вида
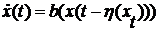(1)
где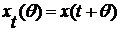 
, 
, 
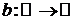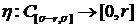, называются дифференциальными
уравнениями с запаздыванием, зависящим от состояния, а именно с сосредоточенным
запаздыванием.
Если заданы начальные
данные в виде
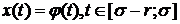(2)
То имеет смысл определить
понятие решения, начинающегося в точке σ с функции φ, или, короче, начинающегося
в φ.
В дальнейшем будем
рассматривать только решения, удовлетворяющие условию Липшица, поэтому следует
дать следующее определение:
Def 1.Функция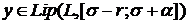 
называется решением
системы (1), (2) на отрезке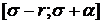 
, если она
удовлетворяет следующим условиям:
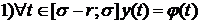
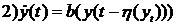на
отрезке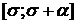 
.
Естественно возникает
вопрос о существовании и единственности такого решения.
Для начала сделаем
некоторые обозначения.
a)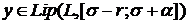 
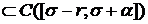есть функция, определенная на отрезке 
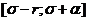и удовлетворяющая условию Липшица с
константой L, то есть
;
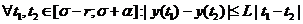b)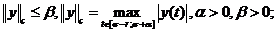 
c)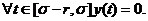
Def 2.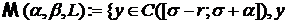
удовлетворяет
условиям a),b),c)}
2. Полезная
лемма
Lemma 1: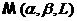 
-выпуклое, замкнутое, ограниченное множество в
пространстве непрерывных на отрезке 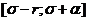функций.
Proof:
1)Выпуклость:
a)Выберем произвольные функции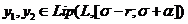 
, тогда
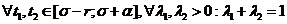
b)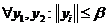
;
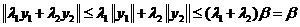c)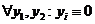
на отрезке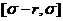 
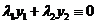на том же отрезке для любых 
.
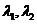2)Ограниченность:
Множество 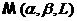определено так, что все элементы этого
множества лежат в шаре радиуса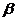 
3)Замкнутость:
Возьмем
последовательность функций такую, что
,
.
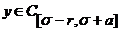a)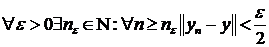
Возьмем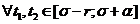 
тогда
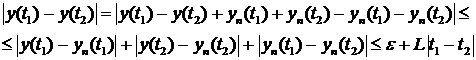
Так как это верно при
любом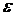 
, то получаем, что предельная функция
удовлетворяет условию Липшица с константой L.
b) По теореме Кантора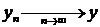 
равномерно на отрезке.
Предположим, что при этом
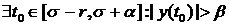(для простоты доказательства предположим
что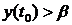 
, если 
,
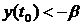рассуждения проводятся аналогично)
Возьмем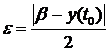 
, тогда, так как для любого
положительного 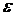и любого 
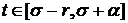выполнено 
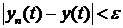, то
выполнено и для данных 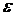и t. Получим:
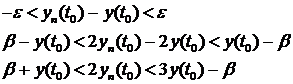
Так как по предположению 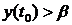, то получаем что 
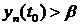, а это невозможно, так как 
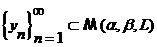. Противоречие показывает, что
предельная функция ограничена по норме той же константой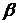 
.
c)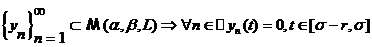 
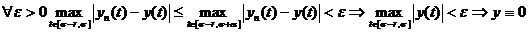
на отрезке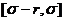 
.
Видим, что выполнение
условий a,b,c равнозначно тому
что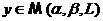 
, то есть множество 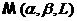замкнуто.
Лемма доказана полностью.
3. Существование
и единственность решения
Для доказательства
теоремы о существовании и единственности липшицевого решения нам потребуется
некоторые понятия и важные теоремы, доказательства которых можно, например,
найти в книге Кадеца [3].
Def 2. Оператор Т называется вполне непрерывным
(компактным), если Т непрерывен и Т отображает любое ограниченное множество в
предкомпактное.
Def 3. Семейство Ф функций φ,
определенных на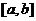 
называется равномерно
ограниченным, если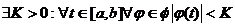 
Def 4.Семейство Ф функций φ, определенных на 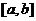, называется равностепенно непрерывным,
если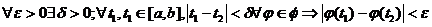 
Теорема 1.(Арцела)
Для того чтобы семейство Ф
непрерывных, определенных на отрезке 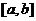функций было
предкомпактом в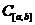 
, необходимо и достаточно, чтобы
это семейство было равномерно ограниченным и равностепенно непрерывным.
Теорема 2.(Шаудера, принцип неподвижной точки)
Если U-замкнутое ограниченное выпуклое
подмножество пространства Банаха X оператор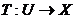 
вполне непрерывен, то Т имеет в U по крайней мере одну неподвижную
точку.
Именно на теореме Шаудера
основано доказательство теоремы о существовании и единственности решения.
Теорема 3.(существование и единственность
решения системы (1).(2))
Пусть система (1),(2)
такая что:
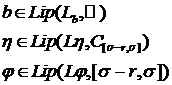
Тогда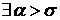 
такая что на отрезке 
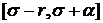существует решение системы (1),(2),
удовлетворяющее условию Липшица, и оно единственно.
Замечание. Для простоты возьмем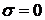 
, для других значений теорема
доказывается аналогично, или сводится к этому случаю заменой переменных.
Доказательство: Проинтегрировав уравнение (1),
увидим, что решение должно удовлетворять условию:
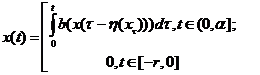
Обозначим
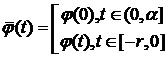
и будем искать решение в
виде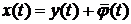 
Где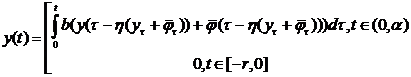 
Определим оператор
,
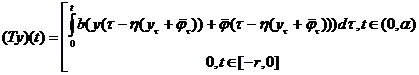Который действует из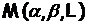 
в себя, действительно, возьмем
произвольный элемент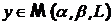 
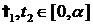
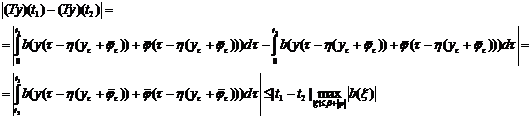
При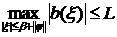 
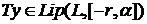
b)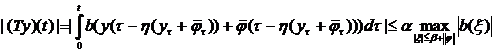 
При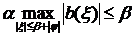 
выполнено 
.
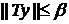c)
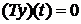при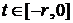 
по
определению оператора.
Выполнение условий a,b,c означает что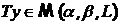 
.
Для этого необходимо
подобрать параметры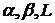 
так, чтоб одновременно
выполнялись условия:
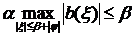(3)
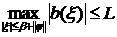(4)
Покажем, что оператор Т
осуществляет непрерывное отображение:
Возьмем
последовательность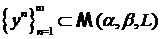 
такую что
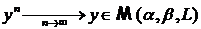
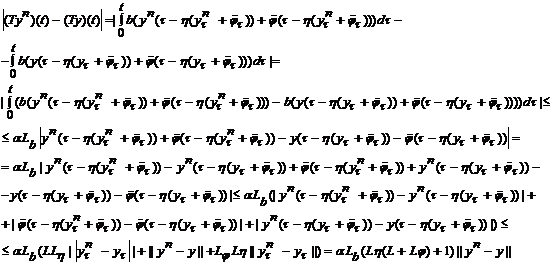
Оценка выполнена на всем
интервале, величина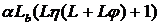 
положительна и конечна,
отсюда следует, что при |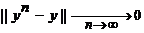
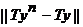также стремится к нулю, а значит
оператор Т переводит сходящиеся последовательности в сходящиеся, а
значит он непрерывен.
Компактность оператора
будем доказывать по теореме Арцела, так как образ оператора лежит в
пространстве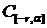 
с соответствующей нормой.
1)
,
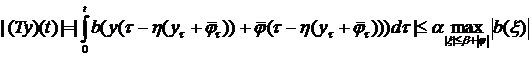правая часть не зависит
ни от t, ни от y, значит образ оператора – равномерно ограниченное семейство функций.
2) 
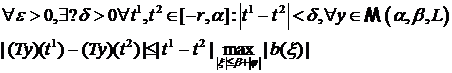
Выбирая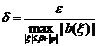 
получаем что образ оператора есть
равностепенно непрерывное семейство функций.
А значит, образ множества
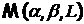предкомпакт, а оператор Т вполне
непрерывен.
Так как множество 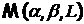ограничено, выпукло и замкнуто, а
оператор Т компактен и действует из этого множества в себя, то по
теореме Шаудера существует по крайней мере одна неподвижная точка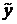 
из этого множества.
,
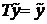а это значит, что 
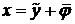- решение системы (1),(2).
Единственность:
Предположим, что при
выполнении условий теоремы x и
y – решения системы (1),(2) на
интервале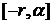 
.
При 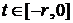оба решении совпадают с начальными
данными, а значит равны между собой. На интервале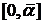 
оценим
модуль разности функций, являющимися решениями.
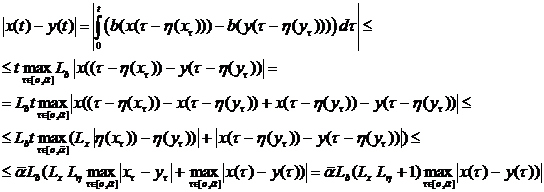
Эта оценка верна для
произвольного t отсюда немедленно следует, что
,
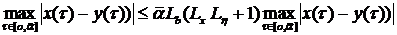Выбирая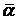 
таким малым, чтоб 
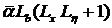было меньше 1, получаем что 
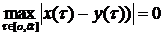, а значит на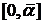 
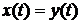. Последовательно строя интервалы
длинной 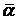закончим доказательство теоремы.
4.Пример
неединственности (Winston)
Для уравнения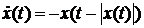 
с начальными данными
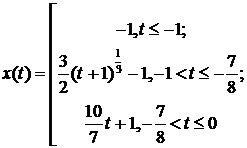
для малых положительных t существует два различных решения:
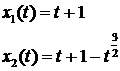
Действительно, проверим,
удовлетворяют ли эти функции уравнению:
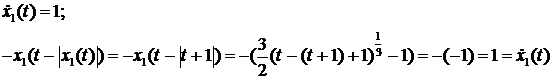
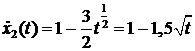
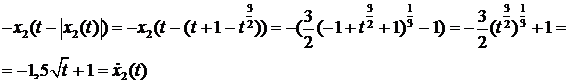
Значит, система имеет два
различных решения. Это происходит потому что при малых t аргумент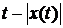 
оказывается
в окрестности -1, а при этих значениях начальные данные недостаточно гладки, не
выполнено условие Липшица.
Список
использованной литературы
[1] HALE J. K. Theory of
functional differential equations. –Berlin; Heidelberg; New York: Springer, 1977.
[2] Резуненко А.В. Краткое введение в обыкновенные
дифференциальные уравнения с запаздывающим аргументом. Харьков-2004.
[3] Кадец В.М. Курс функционального анализа. Харьков-2006.
[4] I.D.Chueshov. Introduction
to the Theory of Infinite-Dimensional Dissipative Systems . «Аста»-2002.
[5] Д. Хенри. Геометрическая теория полулинейных параболических уравнений.
Москва. «Мир»-1985.
[6] Колмогоров А.Н. Фомин С.В. Элементы теории функций и функционального
анализа 1976