Наведення усіх перестановок елементів множини
Міністерство освіти і науки України
Полтавський національний технічний університет
імені Юрія Кондратюка
Факультет інформаційних та телекомунікаційних технологій і систем
Кафедра комп’ютерних та інформаційних технологій і систем
Розрахунково-графічна робота
з дисциплін "Основи дискретної математики"
та "Основи програмування та алгоритмічні мови"
Виконав:
Студент групи
101-ТН
Селін Ігор
Керівник:
д.т.н. Ляхов
Олександр Логвинович
 Полтава 2010
Полтава 2010
Постановка задачі
УМОВА ЗАДАЧІ:
Задано натуральне
число n. Навести всі перестановки елементів множини 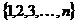 , у яких жоден елемент не залишається на місці.
, у яких жоден елемент не залишається на місці.
Перестановка - це перевпорядкованість наборів елементів, об’єктів
або функція, що задає таку перевпорядкованість.
Множина - це деяка визначена сукупність елементів чи об’єктів.
Розв’язання задачі
G={1,2,3}
(1,2,3) - Так
(1,3,2) - Ні
(2,1,3) - Так
(2,3,1) - Ні
(3,1,2) - Так
(3,2,1) - Ні
З них відповідають
умові задачі лише 3 перестановки. Цього методу можна добитися послідовним
здвигом вправо чисел послідовності. Перше стає на місце другого, друге на
третє, останнє на перше.
Наприклад:
(1,2,3) →
(3,1,2) → (2,3,1)
Алгоритм задачі
Необхідно
визначити яка вхідні та проміжні дані будуть використовуватися.
Насамперед, n-розмірність
множини, тобто факторіал. Також потрібно динамічний масив для
перестановки елементів. Для прорахунку всіх можливих елементів використаємо
цикл із лічильником.
Перший цикл
виводить початкову комбінацію елементів {1…n}.
Другий цикл
виконує nразів перестановку, яка
являється циклом.
Третій цикл -
робить перестановку всіх елементів крім останнього, так як він міняється з
першим. Це робиться "вручну".
Четвертий цикл -
виводить на дисплей результат роботи третього.
Функція swap (int*pointer, int*pointer) має два параметри - вказівники на змінні,
які треба поміняти місцями. Це реалізується через третю змінну. Власне функція ніякого
значення не повертає (void).
Програма
закінчується вивільненням пам’яті та поверненням
повідомлення ОС про правильне закінчення роботи.
Реалізація
програми
#include
<iostream>
void swap (int *px,
int *py)
{
int temp;
temp=*px;
*px=*py;
*py=temp;
}
int main ()
{
int n=0,k;
cout<<"Enter
matrix size: ";
cin>>n;
int *pNums = new
int [n] ;
cout<<"{
";
for (int j=0; j<n;
j++)
{
pNums [j] =j+1;
cout<<pNums
[j] <<" ";
}
cout<<"}"<<endl;
{
for (int i=0; i<n-1;
i++) {
swap (pNums [i],pNums
[i+1]);
}
cout<<"{
";
for (k=0; k<n; k++)
{cout<<pNums
[k] <<" ";
}
cout<<"}"<<endl;
}
cout<<endl;
delete pNums;
cin. get ();
cin. get ();
return 0;
}
Вхідні дані: 11 -
кількість елементів
Вихідні дані: всі
можливі комбінації елементів у вигляді матриці.
Після закуску
програми користувачу необхідно спочатку ввести розмірність матриці N. Цей процес показано далі:
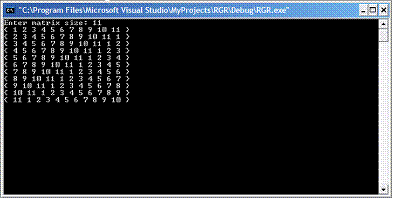
Отже, програма
виводить всі можливі комбінації - їх кількість рівна числу елементів, так як
кожен з них не повинен залишатися на місці.