Матрицы, действия с ними
Контрольная работа на
тему:
«Матрицы, действия с
ними»
1.
Историческая
справка
Понятие Матрица
(в математике) было введено в работах У. Гамильтона и А. Кэли в
середине 19 века. Основы теории созданы К. Вейерштрассом и Ф. Фробениусом
(2-я половина 19 века и начало 20 века). И.А. Лаппо-Данилевский разработал
теорию аналитических функций от многих матричных аргументов и применил эту
теорию к исследованию систем дифференциальных уравнений с аналитическими
коэффициентами. Матричные обозначения получили распространение в современной
математике и её приложениях. Исчисление Матрица (в математике) развивается в
направлении построения эффективных алгоритмов для численного решения основных
задач.
2.
Раскрытие
темы
Понятие о
матрице
Матрица –
множество чисел, образующих прямоугольную таблицу, которая содержит m-строк и n-столбцов. Для
обозначения матрицы используется надпись:
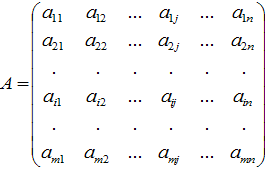
aij, I – номер строки, j – номер столбца.
Элементы
матрицы, стоящие на диагонали, идущие из верхнего левого угла называют главной
диагональю, другую диагональ называют побочной.
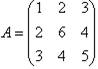пример 1.
Элементы
главной диагонали: 1,6,5. Побочной диагонали: 3,6,3. (пример 1)
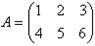пример 2.
Если
количество строк m матрицы не равно количеству столбцов n, то матрица называется
прямоугольной (пример 2).
Если
количество столбцов матрицы совпадают с количеством строк, то матрица называется
квадратной (пример 1).
Количество
строк или столбцов в квадратной матрице называются ее порядком.
Если все
элементы квадратной матрицы, кроме элементов главной диагонали, равны нулю, то
матрица называется диагональной (пример 3).
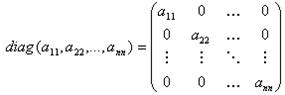пример3
пример 4
Если в
прямоугольной матрице m*n m=1, то получается матрица-строка (пример 5).
xT = (2 3 5).
пример 5.
Если n=1, то получается
матрица-столбец (пример 6).
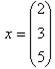пример 6.
Матрицы-строки
матрицы-столбцы называются векторами.
Свойства
матриц:
§
A + (B + C) = (A + B) + C
§
A + B = B + A
§
A(BC) = (AB) C
§
A (B + C) = AB + AC
§
(B + C) A = BA + CA
§
(AT) T
= A
§
(A *
B) T = BT * AT
Действия с
матрицами
1.
Сложение
матриц
Матрицы
одинакового размера можно складывать.
Суммой двух
таких матриц А и В называется матрица С, элементы которой равны сумме
соответствующих элементов матриц А и В. Символически будем записывать так:
А+В=С.
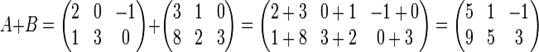
Легко видеть,
что сложение матриц подчиняется переместительному и сочетательному законам:
А+В=В+А
(А+В)+С=А+(В+С).
Нулевая
матрица при сложении матриц выполняет роль обычного нуля при сложении чисел:
А+0=А.
2.
Вычитание
матриц.
Разностью
двух матриц А и В одинакового размера называется матрица С, такая, что
С+В=А
Из этого
определения следует, что элементы матрицы С равны разности соответствующих
элементов матриц А и В.
Обозначается
разность матриц А и В так: С=А – В.
Пример.
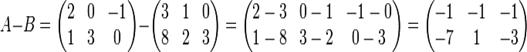
3.
Умножение матриц
Рассмотрим
правило умножения двух квадратных матриц второго порядка.
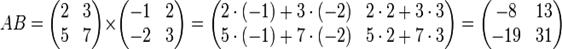
Произведением
матрицы А на матрицу В называется матрица С=АВ.
Правила
умножения прямоугольных матриц:
-
Умножение
матрицы А на матрицу В имеет смысл в том случае, когда число столбцов матрицы А
совпадает с числом строк в матрице В.
-
В
результате умножения двух прямоугольных матриц получается матрица, содержащая столько
строк, сколько строк было в первой матрице и столько столбцов, сколько столбцов
было во второй матрице.
4. Умножение
матрицы на число
При умножении
матрицы A на число a все числа, составляющие
матрицу A, умножаются на число a.
Например, умножим матрицу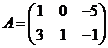 
на число 2. Получим
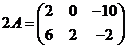, т.е. при умножении матрицы на число
множитель «вносится» под знак матрицы.
5.
Транспонирование
матрицы
Транспонированная
матрица – матрица AТ, полученная из исходной матрицы A заменой строк
на столбцы.
Формально,
транспонированная матрица для матрицы A размеров m*n – матрица AT размеров n*m, определённая как AT[i,
j] = A [j, i].
Например,
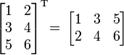
Свойства
транспонированных матриц
1. (AT)T = A
2.
(A + B)T = AT + BT
3.
(AB)T = BTAT
4.
detA = detAT
Список
литературы
1. Баврин, Матросов В.Л. Высшая
математика: Учебник для студентов ВУЗов – М.: 2002.
2. Беллман Р. Введение в
теорию матриц. – М.: Мир, 1969
3. Дж. Голуб, Ч. Ван
Лоун Матричные вычисления. – М.: Мир, 1999.