Депозитарные расписки как способ привлечения инвестиций в российские корпорации
Пензенский государственный университет
Институт информатики и вычислительной техники
Кафедра ИнОУП
КУрсовая работа
Анализ объекта управления «Общежитие»
по дисциплине
«Информационное обеспечение управления»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПГУ 2.032001.11 ПЗ
Выполнил:
студент гр. 04ВД3
М.С. Аптукова
Принял:
ассистент
М.А. Катышева
2007
Реферат
Пояснительная записка содержит 33
страниц, 16 рисунков, 1 таблицу, 11 формул, 2 источника, 2 приложения.
Ключевые
слова: Анализ, система управления (СУ), граф системы управления (ГСУ), матрица,
вершина, дуга, остовное дерево, хорда, канал управления, диаметр графа, ширина
графа, длина пути, характеристический многочлен, вершинная база, связанность
структуры, структурная избыточность, структурная компактность, ранги элементов
структуры, индекс централизации
Целью курсового проектирования
является анализ системы управления «Общежитие » с помощью графоаналитического
(теоретико-графового) метода исследования.
Предметом исследования является
Общежитие.
Содержание
РЕФЕРАТ
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1 СОСТАВЛЕНИЕ ИСХОДНОЙ МОДЕЛИ НА ОСНОВАНИИ ВЕРБАЛЬНОГО ОПИСАНИЯ
ОБЪЕКТА УПРАВЛЕНИЯ «ОБЩЕЖИТИЕ»
2 ПРЕДСТАВЛЕНИЕ СТРУКТУРЫ УПРАВЛЕНИЯ В ВИДЕ ГРАФА
2.1 МАТРИЦА СМЕЖНОСТЕЙ
2.2 МАТРИЦА ИНЦИДЕНЦИЙ
2.3 МАТРИЦА ОСНОВНЫХ КОНТУРОВ
2.4 МАТРИЦА РАССТОЯНИЙ
2.5 МАТРИЦА ДОСТИЖИМОСТЕЙ
2.6 МАТРИЦА ОБХОДОВ
3 АНАЛИЗ ЧИСЛОВЫХ ХАРАКТЕРИСТИК СУ «ОБЩЕЖИТИЕ»
3.1 СТЕПЕНЬ (ПОЛУСТЕПЕНЬ) ВЕРШИНЫ
3.2 ЧИСЛО КОНТУРОВ
3.3 ДЛИНЫ ПУТЕЙ
3.4 ДИАМЕТР И ШИРИНА ГРАФА
3.5 ХАРАКТЕРИСТИЧЕСКИЙ МНОГОЧЛЕН
4 ТОПОЛОГИЧЕСКАЯ ДЕКОМПОЗИЦИЯ СТРУКТУР ОБЪЕКТА
5 СТРУКТУРНО-ТОПОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ
5.1 СВЯЗНОСТЬ СТРУКТУРЫ
5.2 ВЕРШИННАЯ БАЗА
5.3 СТРУКТУРНАЯ ИЗБЫТОЧНОСТЬ
5.4 СТРУКТУРНАЯ КОМПАКТНОСТЬ
5.5 НЕРАВНОМЕРНОСТЬ СВЯЗЕЙ В СТРУКТУРЕ
5.6 СТЕПЕНЬ ЦЕНТРАЛИЗАЦИИ СТРУКТУРЫ
5.7 РАНГИ ЭЛЕМЕНТОВ СТРУКТУРЫ
6 ПОСТРОЕНИЕ КОНТЕКСТНОЙ ДИАГРАММЫ СУ «ОБЩЕЖИТИЕ» ПО МЕТОДУ
ГЕЙНА-САРСОНА С ПОМОЩЬЮ CASE.АНАЛИТИК
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
ПРИЛОЖЕНИЕ А
ПРИЛОЖЕНИЕ Б
Введение
В настоящее время одной из
характерных черт развития общества является возникновение и создание сложных
систем. Для того чтобы изучать такие системы, чтобы их проектировать,
необходимо создать модель системы, модель объекта управления, которая отражает
состав объекта, характер взаимодействия его элементов и их особенности, поэтому
один из главных этапов разработки модели сложных систем, а в частности систем
управления (СУ), состоит в проведении исследований и анализе объекта
управления.
Целью исследования структуры объекта
или СУ является обнаружение критических структурных свойств, которые приводят к
снижению эффективности функционирования СУ. Исследование проводят путем
сравнительного структурного анализа. При сравнении в качестве эталона
используют прототип СУ или стандартные (канонические, типовые) структуры управления
с заранее известными свойствами.
Методы структурного анализа систем
предназначены для исследования как уже имеющихся, функционирующих систем
управления, так и для вновь проектируемых систем. Структурный анализ систем
управления является необходимым этапом для последующего синтеза, т.е. для
создания СУ с заданными свойствами.
На практике важную роль играет
графоаналитический (теоретико-графовый) метод исследования. Этот метод основан
на теории графов и имеет следующие особенности:
- универсальность (унифицированность)
и распространенность;
- наглядность и
интерпретируемость;
- компактность
(лаконичность) представления модели;
- структурность;
- развитость
математического аппарата для количественного анализа;
- хорошую
представимость в ЭВМ.
1
. Составление исходной модели на основании вербального описания
объекта управления «Общежитие»
Исходные данные для построения
модели объекта управления собирались в ходе общения с проживающими,
комендантом, директором студгородка. В результате опроса было сформировано
вербальное описание объекта. Структура описания дает представление о строение
системы. При построении структурного описания определяем список связей между
ними. Атрибутами элемента СУ является их наиболее характерные свойства или
функции. Важную роль играют направление и характер связей. В данной работе
необходимо исследовать те уровни представления структуры СУ, которые
характеризуются информационными связями. Описание структуры «Сбербанк»
представлено в таблице 1.1.
Таблица 1.1- Описание СУ «Общежитие»
|
Элемент системы управления
|
Атрибуты элемента
|
Связи
|
Атрибуты связи
|
Элемент по нотации Гейна-Сарсона
|
|
1 - Ректорат
|
подписание и утверждение приказов
|
Директор студгородка
|
Приказы о заселении
|
Внешняя сущность
|
|
подписание документов
|
Проживающие
|
Договоры
|
|
|
2 - Деканат
|
Предоставление ордера
|
Проживающие
|
Ордер о заселении
|
Внешняя сущность
|
|
3 - Проректор по воспитательной работе
|
Руководство студгородком, проверка общежитий, проведение
промежуточной и итоговой аттестации
|
Комендант
|
Приказы, распоряжения
|
Подсистема
|
|
4 - Директор студгородка
|
Заселение проживающих
|
Проживающие Комендант
|
Приказы Распоряжения, списки проживающих
|
Подсистема
|
Продолжение таблицы 1.1
|
Элемент системы управления
|
Атрибуты элемента
|
Связи
|
Атрибуты связи
|
Элемент по нотации Гейна-Сарсона
|
|
5 - Комендант
|
Составление отчетов и актов Выдача инвертаря Руководство
общежитием (административно- хозяйственной частью) Контролирует деятельность
старост
|
Директор студгородка Проживающие Тех.персонал Староста
общежития
|
Отчеты, акты Паспорт комнаты Распоряжения Распоряжения
|
Подсистема
|
|
6 - Староста общежития
|
Передает поручения. Координирует деятельность старост этажей и
иные виды работ, представляет интересы проживающих Помогает в организации
контроля за сохранностью материальных ценностей
|
Староста этажей Комендант
|
Поручения Акты, докладные, объяснительные
|
Подсистема
|
|
7 - Заместитель по обслуживающим работам (отработке)
|
Следит за своевременным выполнением работ, проверяет
правильность, ведет журнал отработки
|
Комендант
|
Списки отработавших и освобожденных
|
Подсистема
|
|
8 - Старосты этажей
|
Назначают дежурных по этажу, вахте, кухне Контролирует работу
проживающих
|
Староста общежития
|
График дежурств объяснительные, докладные
|
Подсистема
|
|
9 - Старосты комнат
|
Принимают от коменданта комнату, оборудование, имущество
|
Комендант
|
Объяснительные
|
Подсистема
|
|
10 - Проживающие
|
Заключают договор о заселении Пишут заявление о заселении
|
Ректорат Директор студгородка
|
Договоры Заявления, справки
|
Подсистема
|
|
11 - Касса
|
Прием платежей, передача платежных поручений
|
Проживающие
|
Квитанции
|
Внешняя сущность
|
|
12 - Технический персонал
|
Уборка общежития, проведение ремонтных работ
|
комендант
|
Заявления
|
Подсистема
|
|
|
13- Банк
|
Начисление и выдача заработной платы Начисление и выдача
стипендий и платежи за проживание
|
Комендант
|
Чеки, квитанции Чеки, квитанции
|
Внешняя сущность
|
|
|
14 - Пожарная служба
|
Контроль за состоянием противопожарной системы, установка
сигнализации
|
Комендант
|
Инструкции
|
Внешняя сущность
|
|
|
15 - Медицинско-санитарная служба
|
Контроль за содержанием санитарных условий
|
Комендант
|
Инструкции
|
Внешняя сущность
|
|
|
|
|
|
|
|
|
|
|
2
. Представление структуры управления в виде графа
Для моделирования структур СУ удобно
использовать графы. Графом системы управления (ГСУ) называется граф G=G(X,U), в котором множество вершин X
интерпретирует множество элементов СУ, а множество ребер U - множество связей
между ними. Важным преимуществом модели в виде ГСУ является возможность
эффективного применения компьютерных технологий для автоматизации обнаружения
критических структурных свойств исследуемой СУ.
Граф имеет следующие основные формы
представления:
- графический (в виде
диаграммы);
- матричный;
- теоретико-множественный;
- в виде списка.
В данной курсовой работе
используется два первых способа представления графа. Система управления
«Общежитие» в виде диаграммы графа представлена на рисунке 2.1.

Рисунок 2.1 -Диаграмма графа системы управления «Общежитие»
Диаграмма графа иллюстрирует множество точек, расположенных на
плоскости и интерпретирующих вершины графа, и множество жордановых дуг,
соединяющих эти точки и интерпретирующих ребра графа. Граф построен в
соответствии с данными таблицы 1.1. Вершины графа на диаграмме изображены как
окружности с номерами внутри. Нумерация вершин графа совпадает с нумерацией
элементов СУ из таблицы 1.1.
Далее рассмотрим второй способ представления графа - матричный.
Основными матрицами графа являются матрицы смежностей, инциденций и матрица
основных контуров.
2.1 Матрица смежностей
Матрицей смежностей орграфа, имеющего n вершин, называется матрица
A=||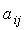 ||n´n,
элемент которой
||n´n,
элемент которой 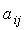 =1,
если вершина i смежна к вершине j (т.е. дуга направлена от вершины i к вершине
j) и
=1,
если вершина i смежна к вершине j (т.е. дуга направлена от вершины i к вершине
j) и 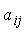 =0
в противном случае. Матрица смежностей ГСУ «Общежитие» представлена на рисунке
2.2.
=0
в противном случае. Матрица смежностей ГСУ «Общежитие» представлена на рисунке
2.2.
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
ρ+
|
|
1
|
|
|
|
|
1
|
|
|
|
|
|
1
|
|
|
|
|
|
|
2
|
|
2
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
1
|
|
3
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
4
|
|
|
|
|
|
1
|
|
|
|
|
1
|
|
|
|
|
|
|
2
|
|
5
|
|
|
|
|
1
|
|
1
|
|
|
|
1
|
|
1
|
|
|
|
|
4
|
|
6
|
|
|
|
|
|
1
|
|
|
1
|
|
|
|
|
|
|
|
|
2
|
|
7
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
8
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
1
|
|
9
|
|
|
|
|
1
|
1
|
|
|
|
|
|
|
|
|
|
|
|
2
|
|
10
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
11
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
1
|
|
12
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
13
|
|
|
|
|
|
1
|
|
|
|
|
1
|
|
|
|
|
|
|
2
|
|
14
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
15
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
ρ-
|
|
0
|
0
|
0
|
3
|
10
|
2
|
0
|
1
|
0
|
6
|
0
|
1
|
0
|
0
|
0
|
|
|
Рисунок 2.2 - Матрица смежностей A
Из данной матрицы можно увидеть, что
сумма всех элементов матрицы равна числу дуг орграфа. Сумма элементов строки i равна полустепени исхода вершины i, а сумма элементов столбца j равна полустепени захода вершины j.
2.2 Матрица инциденций
Матрицей инциденций орграфа, имеющего n
вершин и m дуг, называется матрица B=||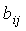 ||n´m,
у которой
||n´m,
у которой 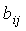 =1,
если дуга j инцидентна вершине i
и направлена от нее,
=1,
если дуга j инцидентна вершине i
и направлена от нее, 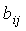 =
-1, если дуга j инцидентна вершине i
и направлена к ней, и
=
-1, если дуга j инцидентна вершине i
и направлена к ней, и 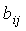 =0
в противном случае. На рисунке 2.3 представлена матрица инциденций ГСУ
«Общежитие».
=0
в противном случае. На рисунке 2.3 представлена матрица инциденций ГСУ
«Общежитие».
|
|
1/4
|
1/10
|
2/10
|
3/5
|
4/5
|
4/10
|
5/4
|
5/6
|
5/10
|
5/12
|
6/5
|
6/8
|
7/5
|
8/6
|
9/4
|
9/5
|
10/5
|
11/10
|
12/5
|
13/5
|
13/10
|
14/5
|
15/5
|
|
|
1
|
|
1
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
-1
|
|
|
|
1
|
1
|
-1
|
|
|
|
|
|
|
|
-1
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
-1
|
-1
|
|
1
|
1
|
1
|
1
|
-1
|
|
-1
|
|
|
-1
|
-1
|
|
-1
|
-1
|
|
-1
|
-1
|
|
|
6
|
|
|
|
|
|
|
|
|
-1
|
|
|
1
|
1
|
|
-1
|
|
|
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
8
|
|
|
|
|
|
|
|
|
|
|
|
|
-1
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
1
|
|
|
|
|
|
|
|
|
|
10
|
|
|
-1
|
-1
|
|
|
-1
|
|
|
-1
|
|
|
|
|
|
|
|
1
|
-1
|
|
|
-1
|
|
|
|
|
11
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
12
|
|
|
|
|
|
|
|
|
|
|
-1
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
13
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
1
|
|
|
|
|
14
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
15
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
Рисунок 2.3 - Матрица инциденций B
2.3 Матрица основных контуров
Матрицей основных контуров орграфа называется матрица С=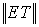 ,
состоящая из подматрицы остовного дерева T
орграфа и единичной подматрицы E,
порядок которой равен числу хорд остовного дерева T.
Остовным деревом называется граф, не имеющий контуров и полуконтуров. Число
основных контуров связного орграфа
,
состоящая из подматрицы остовного дерева T
орграфа и единичной подматрицы E,
порядок которой равен числу хорд остовного дерева T.
Остовным деревом называется граф, не имеющий контуров и полуконтуров. Число
основных контуров связного орграфа 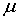 определяется формулой:
определяется формулой:
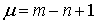 ,
,
где m - число дуг;
n - число вершин.
Согласно этой формуле ГСУ «Общежитие» содержит 9 основных контуров
(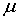 =23-15+1=9).
Остовное дерево ГСУ «Общежитие» представлено на рисунке 2.4, а матрица основных
контуров на рисунке 2.5.
=23-15+1=9).
Остовное дерево ГСУ «Общежитие» представлено на рисунке 2.4, а матрица основных
контуров на рисунке 2.5.
Рисунок 2.4 - Остовное дерево ГСУ «Общежитие»
|
|
1/4
|
4/5
|
4/10
|
5/12
|
6/5
|
8/6
|
9/5
|
10/5
|
13/5
|
1/10
|
2/10
|
3/5
|
5/4
|
5/6
|
5/10
|
6/8
|
7/5
|
9/4
|
11/10
|
12/5
|
13/10
|
14/5
|
15/5
|
|
|
1/4
|
|
1
|
|
|
|
|
|
|
|
|
-1
|
|
|
-1
|
|
1
|
|
|
|
|
|
|
|
|
|
|
4/5
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
4/10
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
1
|
|
-1
|
|
|
|
|
|
|
|
|
|
|
5/12
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
6/5
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
8/6
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
9/5
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
1
|
|
|
|
|
-1
|
|
|
|
|
|
|
|
10/5
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
13/5
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
1
|
|
|
|
|
|
-1
|
|
|
|
Рисунок 2.5 - Матрица основных контуров С
2.4 Матрица расстояний
Матрицей расстояний орграфа называется матрица R=||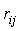 ||n´n, в которой элемент
||n´n, в которой элемент 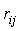 равен длине кратчайшего пути из
вершины i в вершину j.
Если такого пути нет, то соответствующий элемент полагается равным
бесконечности
равен длине кратчайшего пути из
вершины i в вершину j.
Если такого пути нет, то соответствующий элемент полагается равным
бесконечности 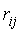 =∞,
а
=∞,
а 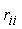 =0.
Матрица расстояний ГСУ «Общежитие» представлена на рисунке 2.6.
=0.
Матрица расстояний ГСУ «Общежитие» представлена на рисунке 2.6.
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
|
1
|
|
|
∞
|
∞
|
1
|
2
|
3
|
∞
|
4
|
∞
|
1
|
∞
|
3
|
∞
|
∞
|
∞
|
|
|
2
|
|
∞
|
|
∞
|
3
|
2
|
3
|
∞
|
4
|
∞
|
1
|
∞
|
3
|
∞
|
∞
|
∞
|
|
|
3
|
|
∞
|
∞
|
|
2
|
1
|
2
|
∞
|
3
|
∞
|
2
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
4
|
|
∞
|
∞
|
∞
|
|
1
|
2
|
∞
|
3
|
∞
|
1
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
5
|
|
∞
|
∞
|
∞
|
1
|
|
1
|
∞
|
2
|
∞
|
1
|
∞
|
1
|
∞
|
∞
|
∞
|
|
|
6
|
|
∞
|
∞
|
∞
|
2
|
1
|
|
∞
|
1
|
∞
|
2
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
7
|
|
∞
|
∞
|
∞
|
2
|
5
|
2
|
|
3
|
∞
|
2
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
8
|
|
∞
|
∞
|
∞
|
3
|
2
|
1
|
∞
|
|
∞
|
3
|
∞
|
3
|
∞
|
∞
|
∞
|
|
|
9
|
|
∞
|
∞
|
∞
|
1
|
1
|
2
|
∞
|
3
|
|
2
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
10
|
|
∞
|
∞
|
∞
|
2
|
1
|
2
|
∞
|
3
|
∞
|
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
11
|
|
∞
|
∞
|
∞
|
3
|
2
|
3
|
∞
|
4
|
∞
|
1
|
|
3
|
∞
|
∞
|
∞
|
|
|
12
|
|
∞
|
∞
|
∞
|
2
|
1
|
2
|
∞
|
3
|
∞
|
2
|
∞
|
|
∞
|
∞
|
∞
|
|
|
13
|
|
∞
|
∞
|
∞
|
2
|
1
|
2
|
∞
|
3
|
∞
|
1
|
∞
|
2
|
|
∞
|
∞
|
|
|
14
|
|
∞
|
∞
|
∞
|
2
|
1
|
2
|
∞
|
3
|
∞
|
2
|
∞
|
2
|
∞
|
|
∞
|
|
|
15
|
|
∞
|
∞
|
∞
|
2
|
1
|
2
|
∞
|
3
|
∞
|
2
|
∞
|
2
|
∞
|
∞
|
|
|
Рисунок 2.6 - Матрица расстояний R
2.5 Матрица достижимостей
Матрицей достижимостей орграфа называется матрица D=||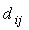 ||n´n, в которой элемент
||n´n, в которой элемент 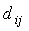 =1, если существует путь из вершины i в вершину j
(т.е. вершина j достижима из вершины i),
иначе
=1, если существует путь из вершины i в вершину j
(т.е. вершина j достижима из вершины i),
иначе 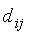 =0,
а
=0,
а 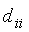 =1.
Матрица достижимостей ГСУ «Общежитие» представлена на рисунке 2.7.
=1.
Матрица достижимостей ГСУ «Общежитие» представлена на рисунке 2.7.
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
|
1
|
|
1
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
2
|
|
|
1
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
3
|
|
|
|
1
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
4
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
5
|
|
|
|
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
6
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
7
|
|
|
|
|
1
|
1
|
1
|
1
|
1
|
|
1
|
|
1
|
|
|
|
|
|
8
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
9
|
|
|
|
|
1
|
1
|
1
|
|
1
|
1
|
1
|
|
1
|
|
|
|
|
|
10
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
11
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
1
|
1
|
|
|
|
|
|
12
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
13
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
1
|
|
|
|
|
14
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
15
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
1
|
|
Рисунок 2.7 - Матрица достижимостей D
2.6 Матрица обходов
Матрицей обходов орграфа называется матрица S=||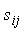 ||n´n, в которой элемент
||n´n, в которой элемент 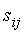 равен длине наибольшего пути из
вершины i в вершину j,
если такого пути нет, то соответствующий элемент полагается равным
бесконечности, т. е.
равен длине наибольшего пути из
вершины i в вершину j,
если такого пути нет, то соответствующий элемент полагается равным
бесконечности, т. е. 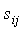 =∞.
Матрица обходов ГСУ «Общежитие» представлена на рисунке 2.8.
=∞.
Матрица обходов ГСУ «Общежитие» представлена на рисунке 2.8.
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
|
1
|
|
∞
|
∞
|
∞
|
3
|
2
|
3
|
∞
|
4
|
∞
|
3
|
∞
|
3
|
∞
|
∞
|
∞
|
|
|
2
|
|
∞
|
∞
|
∞
|
3
|
2
|
3
|
∞
|
4
|
∞
|
1
|
∞
|
3
|
∞
|
∞
|
∞
|
|
|
3
|
|
∞
|
∞
|
∞
|
2
|
1
|
2
|
∞
|
3
|
∞
|
3
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
4
|
|
∞
|
∞
|
∞
|
2
|
2
|
2
|
∞
|
3
|
∞
|
2
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
5
|
|
∞
|
∞
|
∞
|
1
|
2
|
1
|
∞
|
2
|
∞
|
2
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
6
|
|
∞
|
∞
|
∞
|
2
|
1
|
2
|
∞
|
1
|
∞
|
2
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
7
|
|
∞
|
∞
|
∞
|
2
|
5
|
6
|
∞
|
3
|
∞
|
2
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
8
|
|
∞
|
∞
|
∞
|
3
|
2
|
1
|
∞
|
2
|
∞
|
4
|
∞
|
3
|
∞
|
∞
|
∞
|
|
|
9
|
|
∞
|
∞
|
∞
|
2
|
2
|
2
|
∞
|
3
|
∞
|
3
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
10
|
|
∞
|
∞
|
∞
|
2
|
1
|
2
|
∞
|
3
|
∞
|
2
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
11
|
|
∞
|
∞
|
∞
|
3
|
2
|
3
|
∞
|
4
|
∞
|
1
|
∞
|
3
|
∞
|
∞
|
∞
|
|
|
12
|
|
∞
|
∞
|
∞
|
2
|
1
|
2
|
∞
|
3
|
∞
|
2
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
13
|
|
∞
|
∞
|
∞
|
3
|
2
|
3
|
∞
|
4
|
∞
|
2
|
∞
|
3
|
∞
|
∞
|
∞
|
|
|
14
|
|
∞
|
∞
|
∞
|
2
|
1
|
2
|
∞
|
3
|
∞
|
3
|
∞
|
2
|
∞
|
∞
|
∞
|
|
|
15
|
|
∞
|
∞
|
∞
|
2
|
1
|
2
|
∞
|
3
|
∞
|
3
|
∞
|
2
|
∞
|
∞
|
∞
|
|
Рисунок 2.8 - Матрица обходов S
3
. Анализ числовых характеристик СУ «Общежитие»
Для сравнения структурных свойств
различных графов определяют их числовые характеристики (инварианты), которые
выражаются числами или системами чисел, характеризуют определенные свойства и
являются одинаковыми для изоморфных графов. Простейшими инвариантами графа являются
числа его вершин n и дуг m. Ниже будут рассмотрены более сложные числовые характеристики ГСУ
и их интерпретация.
3.1 Степень (полустепень) вершины
Полустепенью исхода вершины орграфа
называется число инцидентных дуг, выходящих из вершины, а полустепенью захода -
число инцидентных дуг, заходящих в вершину. Для определения данной числовой
характеристики используется матрица смежностей (рисунок 2.2), в которой сумма
элементов строки равна полустепени исхода соответствующей вершины, а сумма
элементов столбца - полустепени захода.
Данные характеристики вычисляются по
формулам:
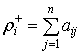 ,
,
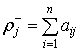 ,
,
где 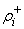 и
и
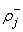 -
полустепени исхода и захода вершин i и j соответственно;
-
полустепени исхода и захода вершин i и j соответственно;
n
- число вершин орграфа;
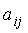 -
элемент матрицы смежностей A.
-
элемент матрицы смежностей A.
Степень 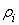 вершины
i определяется как общее число дуг, инцидентных данной вершине, т.е. сложением
полустепеней захода и исхода вершин:
вершины
i определяется как общее число дуг, инцидентных данной вершине, т.е. сложением
полустепеней захода и исхода вершин:
Полустепени исхода и захода вершин для данного графа представлены
в таблице 3.1.
Таблица 3.1
|
Вершины
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
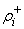 211242112111211 211242112111211
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
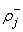 0003102010601000 0003102010601000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
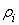 2115144122712211 2115144122712211
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод: по данной числовой
характеристике наиболее загруженным элементом СУ «Общежитие» является
«Комендант», т.е. вершина 5.
3.2 Число контуров
Контуры управления определяют
наиболее устойчивые, охваченные обратной связью, функциональные подструктуры
СУ. С увеличением количества дуг ГСУ число основных контуров увеличивается,
однако значительное увеличение числа основных контуров может привести к таким
неприятным последствиям как, например, уменьшение степени централизации
управления в структуре, т.е. к снижению эффективности управления. Поэтому на
практике полезно исследовать матрицу основных контуров ГСУ (рисунок 2.5),
которая отражает свойства системы всех контуров.
Вывод: ГСУ «Общежитие» содержит 9
основных контуров, причем контуры, определяемые хордами 45;510;512;56;68
являются тривиальными и состоят только из двух дуг. Рассматриваемый ГСУ
содержит также 4 линейно зависимых контура.
3.3
Длины путей
Длина пути между парой вершин в ГСУ
характеризует длину канала управления между соответствующими элементами СУ. С
увеличением длины канала управления увеличивается вероятность искажения
передаваемой информации и уменьшается надежность СУ. Длина пути между вершинами
в ГСУ измеряется числом дуг, составляющих путь. Для характеристики множества
путей в графе используются матрицы расстояний R, достижимостей D и обходов S
ГСУ.
Анализ матрицы расстояний R ГСУ
«Общежитие» (рисунок 2.6) показывает, что максимальную длину 5 имеет путь между
вершинами 7 и 5, т.е. каналы управления между заместителем по обслуживающим
работам и комендантом. Следовательно, между этими отделами существует
вероятность искажения информации.
Анализ матрицы достижимостей D ГСУ
«Общежитие» (рисунок 2.7) показывает, что не все вершины ГСУ являются взаимно
достижимыми (в матрице D есть элементы равные нулю), то есть ГСУ в данном
случае является слабо связным орграфом, что не является положительной
характеристикой структурных свойств СУ.
Из анализа матрицы обходов S ГСУ
«Общежитие» (рисунок 2.8) следует, что наиболее длинный путь между любой парой
вершин в графе не превышает 5.
3.4 Диаметр и ширина графа
Диаметр орграфа L определяется как
наибольшая длина кратчайшего простого пути в графе. Диаметр ГСУ характеризует
подмножество пар элементов СУ, находящихся на самом большом расстоянии друг от
друга, т.е. пар элементов, связанных каналом управления наибольшей длины. Таким
образом, диаметр ГСУ определяет подмножество структурно критических по длине
канала управления пар элементов СУ. Диаметр ГСУ можно определить как наибольший
элемент матрицы расстояний R, например, диаметр ГСУ «Общежитие» определяется
выражением L=5.
Ширина орграфа H определяется как длина максимальной
антицепи, т.е. упорядоченной последовательности попарно несмежных вершин (длина
антицепи на единицу меньше числа ее элементов). Ширина ГСУ «Общежитие»
определяется длиной максимальной антицепи >1,2,11,13,15,14,8,12,7,3,9<,
она является самой длинной по сравнению с другими: >1,5,11,2< или
>10,7,12,6,14,3,15,9<
Вывод: L=5, H=10.
3.5 Характеристический многочлен
Характеристический многочлен 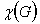 ГСУ определяется символическим
выражением:
ГСУ определяется символическим
выражением:
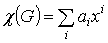 ,
,
где ai
- число вершин со степенью, равной i;
x - символическая (формальная) переменная;
i - степень вершины ГСУ.
Характеристический многочлен 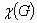 представляет достаточно легко
вычислимый инвариант графа, который позволяет сравнивать свойства различных ГСУ
по числу и степеням вершин.
представляет достаточно легко
вычислимый инвариант графа, который позволяет сравнивать свойства различных ГСУ
по числу и степеням вершин.
Характеристический многочлен ГСУ «Общежитие» выглядит следующим
образом 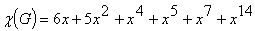 .
.
4
. Топологическая декомпозиция структур объекта
Сильно связный подграф представляет
собой подграф ГСУ, в котором любая пара вершин взаимно достижима. Максимальный
сильно связный подграф образует сильно связную (сильную) компоненту ГСУ,
которая определяет подструктуру СУ, обладающую в определенном смысле лучшими
структурными свойствами по управлению. ГСУ может содержать несколько сильных
компонент, которые выделяются с помощью алгоритма топологической декомпозиции
структуры.
Для определения количества сильных
компонент нужно построить транспонированную матрицу и матрицу Адамара.
Транспонированная матрица - матрица,
получающаяся из матрицы достижимостей D после замены строк, соответствующими
столбцами. Данная матрица обозначается DT.
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
4
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
6
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
7
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
8
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
9
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
10
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
11
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
12
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
13
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 4.1 - Транспонированная матрица DТ
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
11
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
1
|
1
|
|
|
|
|
|
12
|
|
|
|
|
1
|
1
|
1
|
|
1
|
|
1
|
|
1
|
|
|
|
|
|
13
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 4.2 - Матрица Адамара DА
5
. Структурно-топологические характеристики
Для ГСУ вводят следующие специальные
структурно-топологические характеристики, которые легко интерпретируются в
терминах СУ.
5.1 Связность структуры
Связность является свойством, которое определяет такие критические
структурные особенности ГСУ, как наличие несвязных компонент, висячих вершин и
др. Связностью 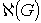 ГСУ
G называется наименьшее число вершин, удаление которых приводит к несвязному
или тривиальному графу.
ГСУ
G называется наименьшее число вершин, удаление которых приводит к несвязному
или тривиальному графу.
Вывод: связность ГСУ «Общежитие» равна 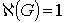 .
Для того, чтобы граф превратился в несвязный можно, например, удалить вершину
под номером 5, т.е. «Комендант».
.
Для того, чтобы граф превратился в несвязный можно, например, удалить вершину
под номером 5, т.е. «Комендант».
5.2 Вершинная база
Вершинная база 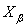 представляет собой минимальное по
мощности множество вершин
представляет собой минимальное по
мощности множество вершин 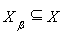 ,
из которого достижимы все вершины ГСУ. Таким образом, вершинная база ГСУ
характеризует минимальный набор элементов СУ, имеющих каналы управления ко всем
остальным элементам.
,
из которого достижимы все вершины ГСУ. Таким образом, вершинная база ГСУ
характеризует минимальный набор элементов СУ, имеющих каналы управления ко всем
остальным элементам.
На основе анализа матрицы Адамара (рисунок 4.2) вершинная база ГСУ
«Общежитие» равна 6.
Качество управления в ГСУ характеризует удельная мощность
вершинной базы ГСУ b, которая определяется по формуле:
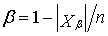 ,
,
где 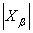 -
мощность вершинной базы;
-
мощность вершинной базы;
n - число вершин ГСУ.
В системе управления «Общежитие»
удельная мощность имеет следующие значение: b = 1-6/15=0,6.
Вывод: качество управления системой
значительно невысокое. По своему значению подходит к несвязной
(децентрализованной) структуре управления.
5.3 Структурная избыточность
Структурная избыточность СУ 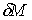 характеризует превышение общего
числа связей над минимально необходимым для обеспечения связности СУ. Величину
характеризует превышение общего
числа связей над минимально необходимым для обеспечения связности СУ. Величину 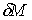 можно
оценить по формуле:
можно
оценить по формуле:
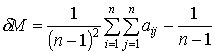 ,
,
где n
- число вершин ГСУ;
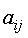 -
элемент матрицы смежностей А ГСУ «Общежитие».
-
элемент матрицы смежностей А ГСУ «Общежитие».
Структурная избыточность ГСУ «Общежитие» равна
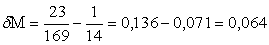 .
.
Вывод: структурная избыточность для данной СУ ближе по своему значению
к 0, т.е. к системе управления с минимальной структурной избыточностью.
Подобную структурную избыточность имеют кольцевые структуры (контуры
управления), и, следовательно, СУ «Общежитие» имеет частично кольцевую
структуру.
5.4 Структурная компактность
Структурная компактность 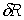 отражает близость элементов
структуры СУ между собой и оценивается выражением:
отражает близость элементов
структуры СУ между собой и оценивается выражением:
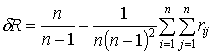 ,
,
где n - число вершин ГСУ;
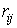 -
элемент матрицы расстояний R ГСУ «Общежитие».
-
элемент матрицы расстояний R ГСУ «Общежитие».
Для того чтобы результат вычислений по формуле был определен,
элементам матрицы расстояний R, равным бесконечности, присваивается конечная
величина n, т.е. вместо 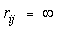 полагают
полагают
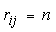 .
.
Структурная компактность ГСУ «Общежитие» равна 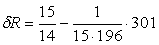 =
=
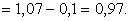
Вывод: данная СУ имеет структурную компактность близкую к
максимальной, что характерно для полного графа.
5.5 Неравномерность связей в структуре
Неравномерность связей в структуре характеризует однородность
(регулярность) структуры управления. Однородные (регулярные) структуры
управления при прочих равных показателях обладают меньшими затратами на
организацию управления и эксплуатацию СУ, так как позволяют экстраполировать
методы организации управления на однородные по структуре фрагменты СУ. Для
оценки однородности структуры управления используется вероятностный подход,
согласно которому любой ГСУ является одной из реализаций случайного орграфа, в
котором множество вершин определено детерминировано, а наличие дуг между
вершинами задано случайным образом. ГСУ «Общежитие» можно рассматривать как
реализацию (одно из возможных значений) некоторого случайного ГСУ, заданного на
множестве из 15 вершин. Неравномерность связей СУ характеризуется выражением 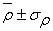 или
нормированным выражением (коэффициентом вариации)
или
нормированным выражением (коэффициентом вариации) 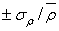 .
Указанные параметры определяются формулами:
.
Указанные параметры определяются формулами:
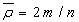 ,
,
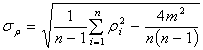 ,
,
где 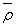 -
средняя степень вершины ГСУ «Сбербанк»;
-
средняя степень вершины ГСУ «Сбербанк»;
m
- число дуг ГСУ;
n
- число вершин ГСУ;
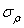 -
среднее квадратическое отклонение;
-
среднее квадратическое отклонение;
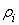 -
степень вершины i.
-
степень вершины i.
Средняя степень вершины ГСУ «Общежитие» равна 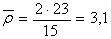 ,
а среднее квадратичное отклонение
,
а среднее квадратичное отклонение 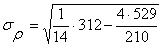 =3,49.
=3,49.
Неравномерность связей ГСУ «Общежитие» имеет приближенное значение
3,1±3,49 или нормированное значение ±1,13.
Вывод: данная СУ приближена к централизованной.
5.6 Степень централизации структуры
Степень централизации структуры ГСУ характеризует близость ее
топологии к стандартной централизованной (или радиальной) структуре СУ. Для
оценки степени централизации структуры вычисляют индекс центральности 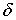 по
следующей формуле:
по
следующей формуле:
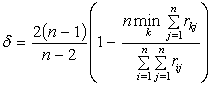
Индекс центральности вычисляется
только для связных неориентированных графов. Так как ГСУ «Общежитие» задан как
орграф, то его следует преобразовать в неориентированный путем дезориентации
дуг и удаления кратных ребер (рисунок 5.1). После этого необходимо построить
матрицу расстояний для неориентированного графа. Данная матрица приведена на
рисунке 5.2.

Рисунок 5.1 - Неориентированный граф
ГСУ «Общежитие»
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
|
1
|
|
0
|
2
|
3
|
1
|
2
|
3
|
3
|
4
|
2
|
1
|
2
|
3
|
2
|
3
|
3
|
|
|
2
|
|
2
|
0
|
3
|
2
|
2
|
3
|
3
|
4
|
3
|
1
|
2
|
3
|
2
|
3
|
3
|
|
|
3
|
|
3
|
3
|
0
|
2
|
1
|
2
|
2
|
3
|
2
|
3
|
2
|
2
|
2
|
2
|
|
|
4
|
|
1
|
2
|
2
|
0
|
1
|
2
|
2
|
3
|
1
|
1
|
2
|
2
|
2
|
2
|
2
|
|
|
5
|
|
2
|
2
|
1
|
1
|
0
|
1
|
1
|
2
|
1
|
1
|
2
|
1
|
1
|
1
|
1
|
|
|
6
|
|
3
|
3
|
2
|
2
|
1
|
0
|
2
|
1
|
2
|
2
|
3
|
2
|
2
|
2
|
2
|
|
|
7
|
|
3
|
3
|
2
|
2
|
1
|
2
|
0
|
3
|
2
|
2
|
3
|
2
|
2
|
2
|
2
|
|
|
8
|
|
4
|
4
|
3
|
3
|
2
|
1
|
3
|
0
|
3
|
3
|
4
|
3
|
4
|
3
|
3
|
|
|
9
|
|
2
|
3
|
2
|
1
|
1
|
2
|
2
|
3
|
0
|
2
|
3
|
2
|
2
|
2
|
2
|
|
|
10
|
|
1
|
1
|
2
|
1
|
1
|
2
|
2
|
3
|
2
|
0
|
1
|
2
|
1
|
2
|
2
|
|
|
11
|
|
2
|
2
|
3
|
2
|
2
|
3
|
3
|
4
|
3
|
1
|
0
|
3
|
2
|
3
|
3
|
|
|
12
|
|
3
|
3
|
2
|
2
|
1
|
2
|
2
|
3
|
2
|
2
|
3
|
0
|
2
|
2
|
2
|
|
|
13
|
|
2
|
2
|
2
|
2
|
1
|
2
|
2
|
3
|
2
|
1
|
2
|
2
|
0
|
2
|
2
|
|
|
14
|
|
3
|
3
|
2
|
2
|
1
|
2
|
2
|
3
|
2
|
2
|
3
|
2
|
2
|
0
|
2
|
|
|
15
|
|
3
|
3
|
2
|
2
|
1
|
2
|
2
|
3
|
2
|
2
|
3
|
2
|
2
|
2
|
0
|
|
|
|
34
|
36
|
31
|
25
|
18
|
29
|
31
|
42
|
29
|
23
|
36
|
31
|
28
|
31
|
31
|
|
Рисунок 5.2 - Матрица расстояний для
неориентированного графа
Индекс центральности ГСУ «Общежитие» равен 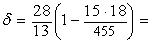
=2,154-0,407=1,747.
Вывод: данная структура управления имеет достаточно высокую
степень централизации.
5.7 Ранги элементов структуры
Ранги элементов структуры позволяют
расположить элементы по иерархическим уровням СУ. Определение рангов вершин ГСУ
выполняется с помощью алгоритма ранжирования или определения порядковой
(ранговой) функции на графе. Алгоритм ранжирования имеет смысл на графе без
контуров, поэтому исходный граф необходимо преобразовать, размыкая имеющиеся
контуры, путем удаления некоторых дуг (рисунок 5.3). В результате проделанных
действий были получены ранги, представленные на рисунке 5.4.

Рисунок 5.3 - ГСУ «Общежитие», преобразованный для алгоритма
ранжирования
В результате выполнения алгоритма,
получим следующее ранжирование вершин: ранг 0 имеют вершины 1,2,11,13,9,3,7,14
и 15, ранг 1 - вершины 5 и 10, ранг 2 - вершины 4,12 и 6, ранг 3 - вершина 8.

Рисунок 5.4 - Расположение элементов СУ «Общежитие» по рангам
6
. Построение контекстной диаграммы СУ «Общежитие» по методу
Гейна-Сарсона с помощью CASE.Аналитик
CASE-Аналитик представляет собой
графическую систему класса CASE, работающую под управлением операционной
системы MS Windows 3.0 и выше.
В основе данной CASE-системы лежит
методология структурного системного анализа Гейна-Сарсона, применимая к
широкому классу систем обработки информации. CASE-Аналитик обеспечивает следующие
возможности:
- средства
для функционального и структурного моделирования исследуемой системы с помощью
диаграмм потоков данных;
- графическое представление модели системы управления в нотации
Гейна-Сарсона;
- автоматическое ведение базы данных проекта;
- автоматическую верификацию проекта, контроль его целостности и
полноты;
- ясное и строгое описание системы (спецификаций системы);
- средства презентации проекта;
- автоматическую генерацию документации на проект;
- автоматическое формирование более 40 видов отчетов и протоколов по
содержанию проекта системы.
Для исследуемой СУ «Общежитие» была
построена контекстная диаграмма, на которой присутствуют внешние сущности,
подсистемы и информационные потоки (таблица 1.1).
Контекстная диаграмма СУ «Общежитие»
была создана с помощью программного средства CASE-Аналитик. При запуске
этой программы открывается диалоговое окно, в котором из пункта главного меню
Проект выбрана команда - Новый. Следующие диалоговое окно предлагает заполнить
поля: Условное наименование - проекта и системы, Руководитель проекта, Хранить
базу данных проекта, Имя директории проекта. Когда эти поля были заполнены, для
запуска проекта требовалось ввести фамилию руководителя проекта - Аптукова и
пароль - 123321. Запустив проект, открывается диалоговое окно с пустым листом,
на которое из пиктоменю помещаются внешние сущности, системы/подсистемы и
информационные потоки их связывающие. Каждому элементу присваивается имя.
Для проведения верификации
необходимо заполнить поля о проекте, исходные данные, разработчики и цели
создания. Пример заполнения этих полей представлен в Приложении Б.
Заключение
В результате проведенного анализа
объекта управления можно сделать ряд выводов о СУ «Общежитие»:
Ÿ наиболее
загруженным элементом данной системы является «Комендант»;
Ÿ СУ «Общежитие»
имеет 9 основных контуров управления;
Ÿ при анализе длин
путей было выяснено, что максимальную длину имеет путь между каналами
комендантом и заместителем по обслуживающим работам, а наиболее длинный путь
между вершинами превышает на 5.
Ÿ В-третьих, на графе
можно выделить 6 сильных компонент.
Ÿ В-четвертых, для
того, чтобы граф превратить в несвязанный, необходимо удалить одну вершину под
номером 5, т.е. элемент комендант.
Ÿ В-пятых, данная
система управления имеет достаточно высокую степень централизации, что можно
увидеть при расчете степени централизации.
Ÿ В идеале, на мой
взгляд, система управления должна сочетать в себе иерархическую и
централизованную структуры управления, где каждый уровень иерархии говорит о
подчинении вышестоящему уровню и руководству над нижестоящими. Для того, чтобы
структура управления стала полностью иерархической и централизованной, нужно
удалить связи между элементами, находящимися на одном уровне и на разных ветвях
иерархии.
Список используемой литературы
1. Лебедев В.Б. «Структурный анализ систем управления», учебное
пособие. - Пенза, 2000.- 96 с.
2. Лебедев В.Б. «Анализ систем управления», методические
указания по курсовому проектированию. - Пенза, 2000.
Приложение А
(обязательное)
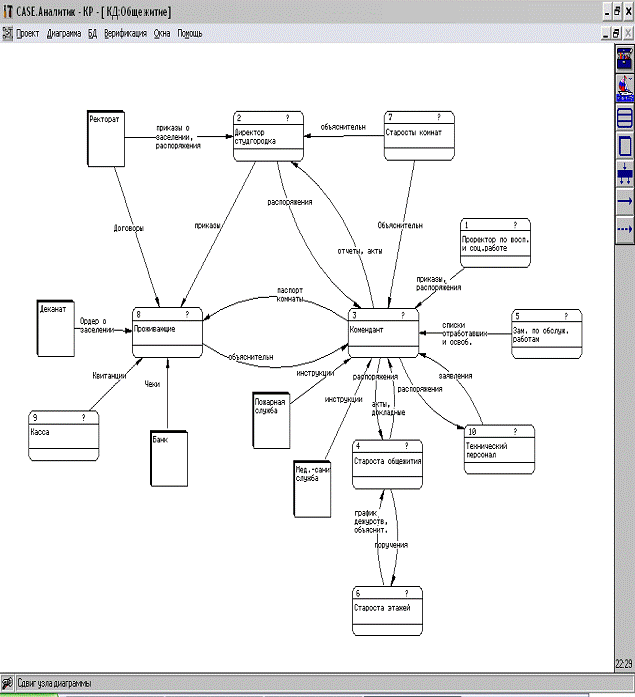
Приложение Б
(обязательное)
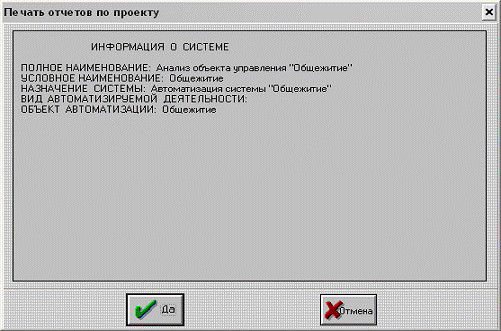
Рисунок Б.1- Отчёт «Информация о системе»
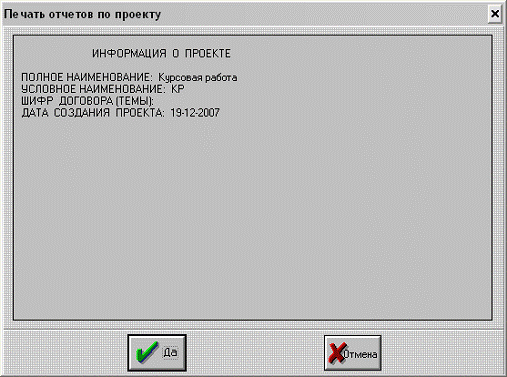
Рисунок Б.2 - Отчёт «Информация о проекте»
Рисунок Б.3 - Отчёт «Разработчики»
Рисунок Б.4 - Отчёт «Цели создания»