3D-Визуализация
Министерство
образования и науки РФ
ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО
ОБРАЗОВАНИЯ
«САРАТОВСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Н.Г. ЧЕРНЫШЕВСКОГО»
Кафедра
материаловедения, технологии и управления качеством
<#"870964.files/image001.gif">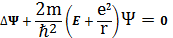
. (1)
Перейдем от декартовых координат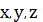 
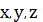к сферическим координатам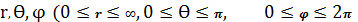 
.
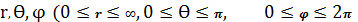Связь между координатами точки, в
которую направлен радиус-вектор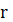 
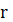в разных системах, описывается
следующим образом:
,
;
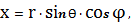
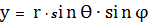
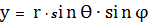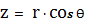
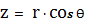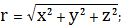
Переход к сферической системе
координат позволяет представить волновую функцию в виде произведения:
,
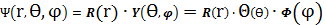
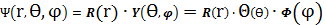радиальной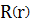 
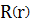и угловой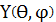 
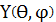частей.
Такое представление волновой функции
позволяет разбить уравнение Шредингера для атома водорода на три уравнения в
сферических координатах. Решая эти уравнения по отдельности, можно получить
волновую функцию и рассчитать возможные значения энергии атома водорода.
Изменение угла φ может
рассматриваться, как вращение электрона в плоскости, которое описывается
уравнением бегущей волны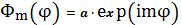 
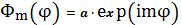. Согласно условию однозначности
волновой функции, один полный оборот приводит систему в исходное положение, в
итоге:
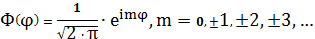
В атоме угловой механический момент
электрона жестко связан с вектором магнитного момента, энергия которого во
внешнем магнитном поле зависит от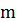 
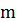. Поэтому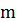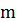называется магнитным квантовым
числом. Это число определяет возможные проекции вектора углового момента
электрона на ось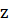 
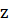, то есть ориентацию механического
углового момента электрона в пространстве. В силу целочисленности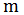 
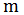, эти проекции дискретны.
Зависимость от угла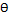 
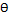имеет вид:
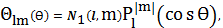
где,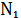 
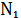- множитель, зависящий от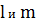 
; 
, 
.
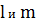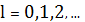
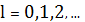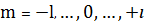
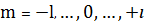Решение для угловой части уравнения
Шредингера для атома водорода имеет следующий вид[3]:
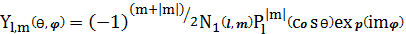
Комплексные функции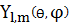 
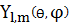называются сферическими
гармониками.
Для конкретного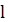 
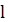имеется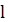 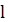поверхностей, проходящих через
положение ядра, где функция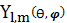 
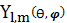обращается в нуль, они называются
узловыми поверхностями или просто узлами. Вероятность найти электрон в узле
равна нулю. Таким образом, для каждого 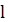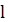имеются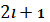 
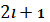сферических гармоник, отличающихся
положением в пространстве узловых поверхностей, квантовое число 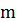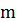определяет ориентацию узловых
поверхностей.
Наличие узловых поверхностей у волновой функции
атомов связано с волновыми свойствами электронов. В любой волне имеются точки,
в которых смещение колеблющейся величины равно нулю, а в случае, когда
колебания происходят в трех измерениях, совокупность этих точек образует
узловую поверхность.
волновой атом график электрон
2. Практическая часть
Построить график функции 4d-орбиталь
(l=2,m=0).
Итак, преступим к решению нашей задачи:
) Зададим диапазон аргумента и ординаты (Xmin;
Xmax;Ymin;Ymax).
) Затем определимся с количеством разбиений
нашего аргумента (N).
3) Выведем формулу. Пусть x будет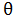 
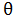, а y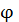 
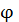,тогда для (l=2, m=0) получается
формула следующего вида[4]:
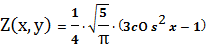(2)
) Приступаем к реализации этой формулы в среде
LabView.
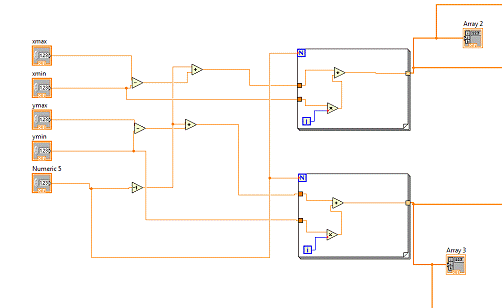
Рисунок 1 - Циклы Forloop
для перебора x и y
) Для перебора всех x
и y используем цикл
Forloop, который
позволяет перебрать все значения Xi и Yi
от 0 до N. Получившиеся значения сохраняем в массивах Array
2 и Array 3.
Теперь, когда у нас есть значения Xi иYi,
приступаем к нахождению Zi.
) Создадим цикл Forloop
и внутрь которого вложим еще один цикл Forloop
и реализуем формулу (1) для нахождения Zi.
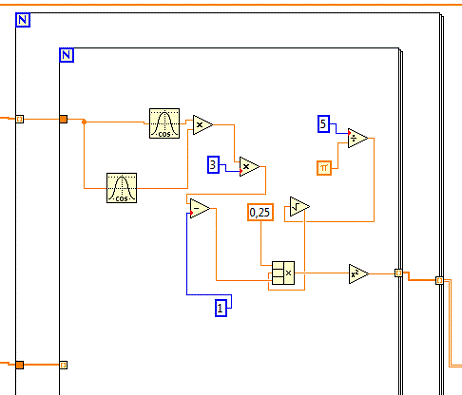
) Включаем индексацию, для того чтобы все x
перебрались относительно y,
а yотносительно x.
) На выходе создаем массив Array
и записываем в него все получившие значения Zi.
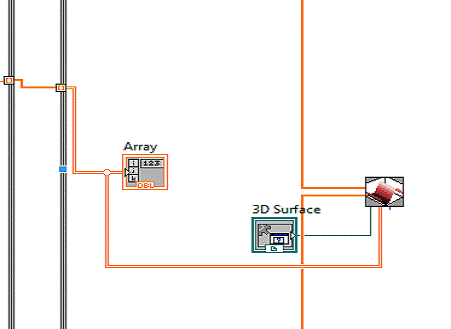
Рисунок 3 - Массив Arrayи
3DSurface
9) Подключаем массивы Zi
,Yi ,Xi
к 3DSurface и получим график.
Заменим систему координат на сферическую:
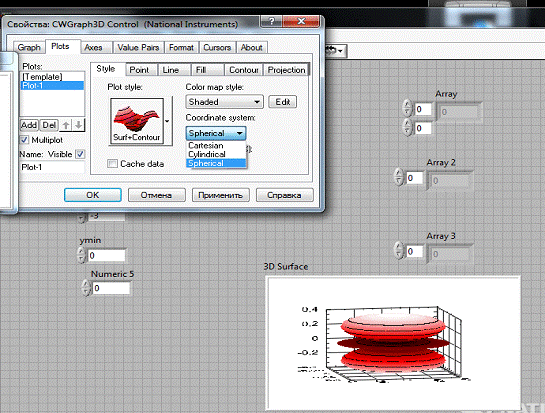
Рисунок 4 - Замена системы координат
Так выглядит решение на блок-диаграмме:
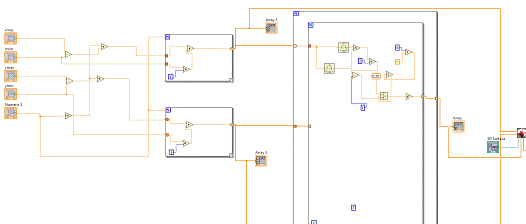
Рисунок 5 - Формула на блок диаграмме
Заключение
В ходе осуществления данной
работы были решены поставленные задачи, и построен график 3D4d-орбитали
(l=2, m=0). Были получены навыки построения трехмерных графиков и замены
системы координат.