Программное обеспечение вычислений
Введение
Borland
C++ Builder
- выпущенное компанией Borland
средство быстрой разработки приложений, позволяющее создавать приложения на
языке C++, используя при
этом среду разработки и библиотеку компонентов такую же, как в Delphi.
Можно отметить ряд положительных аспектов разработки приложений в С++ Builder:
удобство визуального конструирования приложений, развитые возможности доступных
средств системы, эффективность генерируемого кода и другие.
Язык программирования C++ широко используется
для разработки программного обеспечения. А именно, создание разнообразных
прикладных программ, разработка операционных систем, драйверов устройств, а
также видео игр и многих других программных продуктов. Помимо Borland
C++ Builder
существует ещё несколько реализаций языка программирования C++ - как
бесплатных, так и коммерческих. Их производят проекты: GNU, Microsoft и другие.
Проект GNU - проект разработки свободного программного обеспечения (СПО).
1. Постановка задачи
Составить схему алгоритма и программу для построения
графика временной функции, работающую как в машинном, так и в реальном времени.
Реальное время в диапазоне (t0
-
tкон)
формируется таймером в виде программного модуля с метками Тк,
называемыми временем квантования. При вычислении функции использовать алгоритм
Горнера.
Функция:
Z = | at4
+
bt3 +
ct2 +
dt + k
+ m |,
где t0
=
0 с; tкон =
10 с; Tк =
0,5 с;
k - корень
нелинейного уравнения x2
= sin5x,
которое надо решить методом Ньютона с точностью 
,
при начальном значении x0
= 0,58;
m - разность корней
квадратного уравнения:
a1z2 + b1z
+ c1 = 0
при a1 =
1, b1 = 5, c1 = 6.
Коэффициенты:=
0, b = 1, d = |b-c|, c = sin 45o.
2. Методы расчета
.1 Метод Ньютона
В основе метода лежит разложение функции в ряд
Тейлора
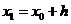. Для нахождения h
используем ряд Тейлора:
График 1. Метод Ньютона
Из графика 1 видно, что при переходе от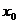 
,
и
т.д. значение у=f(x)
приближается к 0.
В ряде Тейлора члены с 
и
выше отбросим и в итоге получается:
.
Можем записать следующее выражение:
и тогда рабочая (итерационная) формула будет
иметь вид:
.
Эту же формулу можно получить другим способом.
Пусть имеем 
,
корень уравнения х* находится на [a,b],
при этом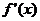 
и
сохраняют
определённые знаки. Геометрически метод Ньютона эквивалентен замене некоторой
дуге 
касательной,
проведенной в некоторой точке кривой. Допустим, что >0
при 
.
- уравнение
касательной. Согласно задаче примем y=0,
,
и тогда рабочая формула будет иметь вид:
.
В данном методе, как и в методе простой
итерации, очень важно выбрать 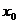. Условие выбора
начального приближения является условие 
.
Счёт заканчивается в том случае, если выполняется условие 
.
Алгоритм нахождения корня:
) Выбираем .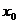
) -
нахождение последовательного приближения корня.
3) Счёт заканчивается, когда выполняется условие
.
Метод обладает квадратичной скоростью
сходимости.
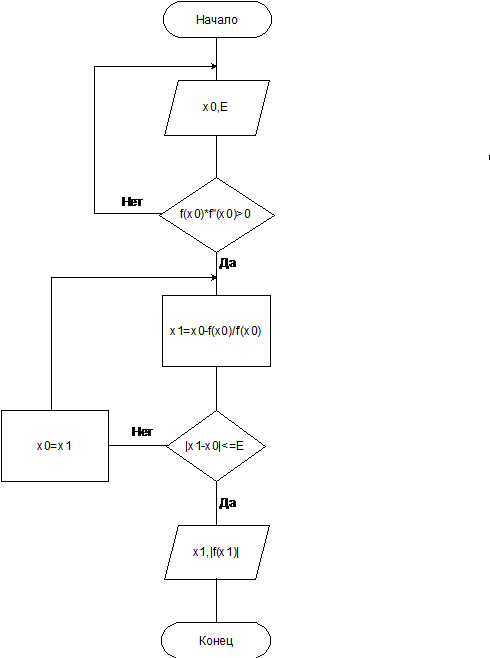
Блок-схема 1. Метод Ньютона
2.2 Метод простых итераций
Суть метода заключается в следующем: исходное
уравнение заменяем
эквивалентным 
. Выбрав начальное
приближение 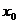, будем
последовательно производить вычисления:
и продолжать будем до тех пор пока 
.
В данном методе очень важно выбрать начальное
приближение 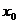. Если это будет
сделано не верно, то итерационный процесс будет расходящимся, т.е. с каждой
итераций мы не приближаемся к корню, а наоборот удаляемся и в этом случае
получаем бесконечный цикл. Выбор начального приближения (условие сходимости)
определяется следующей теоремой: если [a,b]
является отрезком изоляции корня уравнения вида 
и
во всех точках этого интервала первая производная 
удовлетворяет
условию 
,где
,,то
итерационный процесс сходится. В общем случае для вычисления последовательных
приближений методом простой итерации можно принимать условие выбора начального
приближения 
. Скорость
сходимости метода тем выше, чем меньше 
.
Блок-схема 2. Метод простых итераций
.3 Метод деления пополам
График 2. Метод деления пополам
Рассмотрим график 2. В нём представлена суть
метода: делим заданный отрезок [а, b] пополам, находим c = (a
+ b) / 2. Получили 2
отрезка [а, с] и [b, с]. Далее надо определить на каком из полученных отрезков
находится корень, используя нахождения корня на отрезке. f(a)*f(c)
< 0 -> [а, с], иначе -> [с, b]. Далее применяем тот же приём деления
отрезка пополам, тому из отрезков, на котором находится корень. Снова проверяем
условие нахождения корня на отрезке и продолжаем этот процесс до тех пор, пока
полученный отрезок будет настолько мал, что любая точка из этого отрезка нам
будет подходить в качестве корня.
Алгоритм нахождения корня:
) f(a)
* f(b)
< 0 - имеем корень.
2) c = (a + b) / 2.
) Если
f(a) * f(c) < 0 ,то
b = c.
Если f(b)
* f(c)
< 0 , то а = с.
) |a
- b| < E;
Метод обладает линейной скоростью сходимости. За
одну итерацию точность возрастает в 2 раза.
Блок-схема 3. Метод бисекции
2.4 Метод хорд
Метод хорд является более быстрым способом
нахождения корня уравнения f(x)=0,
лежащего на отрезке [а, b]. Для получения итерационной формулы нахождения
приближенных значений корня. Для большей наглядности рассмотрим случай, когда
f(a)<0.
-ый способ: Пусть f(a)<0,
f(b)>0.
Разделим отрезок [а, b] в отношении f(a)/f(b).
Из графика 3 видно, что первое приближение корня x1=a+h1.
Для нахождения h рассмотрим подобные треугольники ABC и Aax1
, 
.
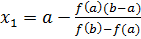Рассматривая [a;x1]
и [x1;b]
и применяя тот же приём, который рассматривали выше, ищем h2
и т.д.
-ой способ: Геометрически, метод хорд
эквивалентен замене дуги y=f(x)
хордой проходящей через точки А и B.
В этом случае уравнение хорды можно записать как
.
Принимаем, что х=х1 и у=0, и тогда из
уравнения хорды можно получить:
.
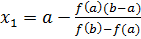Алгоритм нахождения корня:
) 
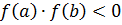- имеем корень.
иначе x0
= b;
) Если f(a)<0,
то 
,
иначе 
;
) Счёт заканчиваем, когда. 
График 3. Метод хорд
Блок-схема 4. Метод хорд
2.5 Схема Горнера
Схема Горнера предназначена для вычисления
значений многочлена, записанного в виде суммы одночленов, при заданном значении
переменной.
Есть полином вида:
Нужно вычислить его значение.
В схеме Горнера исходный полином представляется
в виде:
Выражение 
обозначим
,
и рекуррентная формула будет иметь следующий вид:
.
Значение полинома получается после выполнения n
вычислений.
Блок-схема 5. Схема Горнера
3. Код программы
#include
<vcl.h>
#include
<math.h>
#include
<windows.h>
#pragma hdrstop
#include
"Unit1.h"
#pragma
package(smart_init)
#pragma resource
"*.dfm"
#define pi
3.141592653*Form1;a1 = 1, b1 = 5, c1 = 6, a = 0, b = 1, c = sin(45*pi/180), d,
tK = 0.5, tKon = 10, t0 = 0, E = 0.001, x0, x1, m, t, k, cfs[6], y;i, n;
__fastcall
TForm1::TForm1(TComponent* Owner)
: TForm(Owner)
{
}
// Функция f. Нелинейное
уравнение x^2 = sin5x. (исходное уравнение)f (float x)
{(sqrt(fabs(sin(5*x))))-x;
}
// Функция fp. Производная от
функции f. (для метода Ньютона)
float fp (float x)
{((5*cos(5*x))/(2*sqrt(fabs(sin(5*x)))))-1;
}
// Функция f1. Функция f с
переменной x, перенесённой в левую часть. (для метода простых итераций)f1
(float x)
{sqrt(fabs(sin(5*x)));
}__fastcall
TForm1::BitBtn1Click(TObject *Sender) // Нажатие на кнопку "ОК"
{= 0.001; // Границы интервала= 0.58; // поиска корней=
fabs(b-c); // Задание значения переменной d= 0; // Обнуление переменной
счётчика итераций->Clear(); // Очистка графика
// Решение квадратного уравненияD, z1, z2;
D = pow(b1,2) - 4 *
a1 * c1;= (-b1 - sqrt(D)) / (2 * a1);= (-b1 + sqrt(D)) / (2 * a1);= fabs (z2 -
z1);
// Вывод разности его корней->Caption=(FloatToStrF(m,ffFixed,8,3));
switch (RadioGroup1->ItemIndex) // Выбор метода решения в
зависимости от индекса RadioGroup1
{
// Решение нелинейного уравнения методом Ньютона0:
x1 = x0 - f(x0) /
fp(x0);
while(fabs(f(x1-x0))
> E)
{
if(n!=0) x0 = x1;
x1 = x0 - f(x0) /
fp(x0);
n++;
}= x0;;
// Решение нелинейного уравнения методом простых итераций
case 1:
{(n!=0) x0 = x1;=
f1(x0);++;
}((fabs(f1(x1)-f1(x0)))
>= E);
k = x1;;
// Решение нелинейного уравнения методом деления пополам
case 2:xm, xd;=
x1-x0;= x0+xd;(xd >= E)
{++;= xd/2;=
x0+xd;(f(x0) * f(xm) < 0)= xm;= xm;
}= xm;
break;
// Решение нелинейного уравнения методом хорд
case 3:
do
{
if (n!= 0) x0h =
x1h;
if (f(x0)<0) x1h
= x0h - ((f(x0h)*(x1 - x0h))/(f(x1) - f(x0h)));
else
x1h = x0h -
((f(x0h)*(x0h - x0))/(f(x0h) - f(x0)));
n++;
}
while (fabs(x1h -
x0h) > E);
*/= 0.563656; // Должно быть x1h, но метод не работает с этим
уравнением;
}
// Вывод результатов на
экран->Caption=(FloatToStrF(k,ffFixed,8,3));
Label19->Caption=("Проверка, f(x )= " +
FloatToStrF(f(k),ffFixed,8,5));->Caption=("Итераций: "+ IntToStr(n));
// Схема Горнера. Занесение коэффициентов в массив
cfs[1] = a;[2] =
b;[3] = c;
cfs[4] = d;[5] = k+m;
// Цикл для вычисления значений многочлена с зависимостью от
времени
for (float
t=t0;t<=tKon;t=t+tK)
{= fabs(cfs[1]);(i
= 2;i <= 5;i++)
{
y = fabs(y*t +
cfs[i]);
}(RadioButton1->Checked==false) // Условие для построения
графика в реальном времени
{->AddXY(t,y); // Добавление точки на график(tK*1000); //
Ожидание, мс (время квантования)
Application->ProcessMessages();
}Series1->AddXY(t,y);
// Построение графика в машинном времени
}
}__fastcall
TForm1::RadioGroup1Click(TObject *Sender)
{->Clear(); // Очистка графика при смене типа вывода
}
//---------------------------------------------------------------------------
4.
Результаты
.1
Скриншоты
Рисунок
1. Вид программы
Рисунок
2. Результат выполнения программы в машинном времени с решением уравнения
методом Ньютона
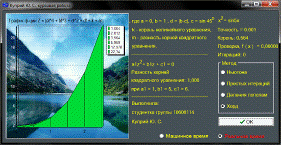
Рисунок
3. Промежуточный результат выполнения программы в реальном времени с решением
уравнения методом хорд
Вывод
программа график уравнение
С
помощью выполнения данной курсовой работы я закрепила навык создания программ в
Borland C++ Builder 6.0. Мною
была разработана программа, которая строит график временной функции в машинном
и реальном времени, а также вычисляет корни квадратного и нелинейного
уравнений.
Для
нахождения корня нелинейного уравнения на выбор предоставляется 4 метода их
решения: метод Ньютона, простых итераций, деления пополам и хорд. Каждый из
методов имеет свои положительные и отрицательные стороны.
Список
использованной литературы
1. Конспект лекций по информатике.
. Архангельский А. Я. «C++ Builder
6. Справочное пособие. Книга 1. Язык С++»
3. Рейхсдорф
К.,
Хендерсон
К.
«Borland C++ Builder. Освой самостоятельно»
4. Культин Н. «C++
Builder в задачах и
примерах»