Методы принятия управленческих решений

Методы принятия управленческих решений

Методы принятия управленческих решений

Задание

Цель работы.

Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.

Порядок выполнения.

.Вводим исходные данные.

Переменным задачи соответствуют ячейки:

B3(x1); C3(x2); D3(x3); E3(x4); F3(x5).

Коэффициентам ЦФ соответствуют ячейки:

B5(c₁=84); C5(c₂=5.7); D5(c₃=0); E5(c₄=10); F5(c₅=-3).

Правым частям ограничения соответствуют ячейки:

I9(b₁=50); I10(b₂=120); I11(b₃=600); I12(b₄=210).

. В ячейку G5 вводим формулу, по которой будет рассчитываться значение целевой функции.

Целевая функция определяется выражением:

x₁+5.7x₂+10x₄-3x₅

В ячейку G5 вводим формулу и нажимаем Enter

=СУММПРОИЗВ(B3:F3;B5:F5).

В ячейку G9 вводим формулу и нажимаем Enter

В ячейку G10 вводим формулу и нажимаем Enter

=СУММПРОИЗВ(B10:F10;B3:F3)

В ячейку G11 вводим формулу и нажимаем Enter

=СУММПРОИЗВ(B11:F11;B3:F3)

В ячейку G12 вводим формулу и нажимаем Enter

=СУММПРОИЗВ(B12:F12;B3:F3)

.Устанавливаем параметры решения задачи. (В окне «Поиск решения»)

В графу «Установить ячейку» вводим $G$5 и приравниваем к максимальному значению. В поле «Изменяя ячейки» вписываем адреса $B$3:$F$3. В поле «Ограничения» вписываем все ограничения целевой функции:

$B$3>=0; $C$3>=0; $D$3>=0; $E$3>=0; $F$3>=0; $G$10<=120; $G$11=600; $G$12>=210; $G$9=50.

.Решение задачи.

В окне «Поиск решения» нажимаем «Выполнить» получаем сообщение о решении задачи.

Ответом данной задачи линейного программирования являются следующие значения:

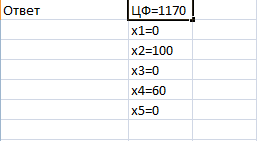
Вывод

линейный программирование excel

При выполнении данной работы я научилась решать задачи линейного программирования с помощью Microsoft Excel.

Для того чтобы решить задачу линейного программирования необходимо выполнить следующие действия.

1.      создать экранную форму для ввода условия задачи.

.        ввести исходные данные в экранную форму.

.        ввести зависимости из математической модели в экранную форму.

.        задать ЦФ.

.        ввести ограничения и граничные условия.

.Решить задачу:

.        установить параметры решения задачи.

.        запустить задачу на решение.

.        выбрать формат вывода решения.