Использование АОС 'Транспортная задача'

Использование АОС 'Транспортная задача'

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ «ГОРНЫЙ»

КАФЕДРА ИНФОРМАЦИОННЫХ СИСТЕМ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Использование АОС «Транспортная задача»

Санкт-Петербург

Цель работы

Целью данной лабораторной работы является решение математической задачи, которая представлена в виде модели транспортной задачи.

Задание

Решить транспортную задачу методом потенциалов, используя АОС.

Согласно УМК условия задания (таблица №1) выбираются студентом самостоятельно и согласовывается с преподавателем каждым студентом индивидуально.

Таблица №1. Условия математической транспортной задачи для ее решения методом потенциалов

Решение

Математическая модель транспортной задачи: F = ∑ ∑ c_ijx_ij, (1), при условиях:

∑ x_ij = a_i при i = 1, 2,…, m, (2) и ∑x_ij = b_j при j = 1, 2, …, n, (3).

С целью составления двойственной задачи переменные x_ij в условии (2) заменим на u₁, u₂, u_i, ..., u_m, а переменные x_ij в условия (3) на v₁, v₂, v_j,..., v_n.

Поскольку каждая переменная x_ij входит в условия (2,3) и целевую функцию (1) по одному разу, то двойственную задачу по отношению к прямой транспортной задаче можно сформулировать следующим образом.

Требуется найти не отрицательные числа u_i (при i = 1, 2, …, m) и v_j (при j = 1, 2, …, n), обращающие в максимум целевую функцию: G = ∑ a_iu_i + ∑ b_jv_jпри условии:

u_i + v_j ≤ c_ij, i = 1, 2, ..., m; j = 1, 2, ..., n (4).

В систему условий (4) будет mxn неравенств. По теории двойственности для оптимальных планов прямой и двойственной задачи для всех i, j должно быть: u_i + v_j ≤ c_ij, если x_ij = 0, u_i + v_j = c_ij, если x_ij ≥ 0,

Эти условия являются необходимыми и достаточными признаками оптимальности плана транспортной задачи.

Числа u_i , v_j называются потенциалами. Причем число u_i называется потенциалом поставщика, а число v_j - потенциалом потребителя.

Для упрощения решения математической транспортной задачи воспользуемся программным комплексом «АОС транспортная задача» разработанным студентом Сорокиным Д.Ю.

.По первой теореме двойственности в оптимальном решении значения целевых функций прямой и двойственных задач совпадают: F = G.

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов в таблице №1 и отображена на рисунке №1.

транспортный задача потенциал поставка

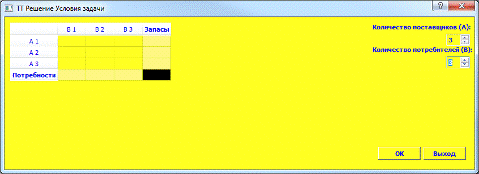
Рисунок №1. Ввод исходных данных задачи в программу «АОС транспортная задача»

Проверим необходимое и достаточное условие разрешимости задачи:

∑_a = 25+25+25= 75

∑_b = 30+25+20= 75

Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.

.Решим задачу диагональным методом или методом северо-западного угла

Благодаря программе «АОС транспортная задача» автоматически получен первый опорный план рисунок №2, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

Рисунок №2. Первый опорный план и проверка целевой функции

3.Подсчитаем число занятых клеток таблицы на рисунке №2.

Количество занятых клеток равно 5, а должно быть m + n - 1 = 5. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

(x) = 700

4.Проверим оптимальность опорного плана путем поиска предварительных потенциаловu_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

Благодаря программе «АОС транспортная задача» найдем предварительные потенциалы.

Результат поиска потенциалов отобразим на рисунке №3.

Рисунок №3. Результат поиска предварительных потенциалов в программе «АОС транспортная задача»

5.Проверим результат поиска предварительных потенциалов путем вычисления невязок.

С помощью программы «АОС транспортная задача» вычислим невязки.

Рисунок №4. Результат вычисления невязок в программе «АОС транспортная задача»

. Согласно полученным результатам на рисунке №4, выходит, что все потенциалы не равны нулю, следовательно,u_i + v_i>c_ij,тогда предложенный план не оптимален.

Следовательно, нажимается кнопка «Нет».

. На рисунке №5, программа «АОС транспортная задача» просит ввести «Координаты перевозки, вводимый в базис».

Рисунок №5. Ввод координат перевозки, вводимый в базис

. Произведем ввод «координаты перевозки, вводимый в базис», которые в данном случае будут: A(i) = 3 и B(j)= 1.

Ввод «координат перевозки, вводимый в базис» в программе «АОС транспортная задача» изображен на рисунке №6.

. В следующем окне программа «АОС транспортная задача» построит цикл поставок рисунке №7.

Рисунок №6. Ввод координат перевозки, вводимый в базис

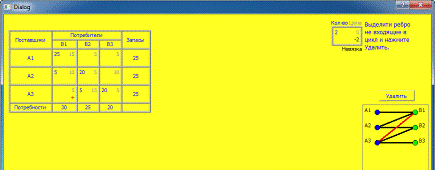
Рисунок №7. Цикл поставок

Рисунок №8. Цикл поставок с удаленными ребрами

. В следующем окне (рисунке №7) программа «АОС транспортная задача» построит цикл поставок.

. Для дальнейшего решения задачи требуется в окне программы «АОС транспортная задача» выделить все ребра, которые не входят в цикл и удалить их.

В результате этих удалений получится цикл рисунок №8.

. Введем знаки для клетокA(2)B(2), А(2)В(3) и А(3)В(3).

В результате ввода знаков для клетокполучается, что значение клеток A(2)B(2) иА(3)В(3) отрицательное, а значение клеток A(2)B(3) и A(3)B(2) положительное, что изображено на рисунке №9.

Рисунок №9. Результате ввода знаков клетокA(2)B(2), А(2)В(3) и А(3)В(3)

. Выберем из клеток A(2)B(2)и А(3)В(3) минимальное количество товара, которое равняется 5, т.е. это значение находящиеся в клетке А(2)В(3).

Введем данное значение в поле «Из клеток помеченных знаком «-» выберите MIN значение».

В результате всех выше описанных действий с программой «АОС транспортная задача» получился новый опорный план, который изображен на рисунке №10.

Рисунок №10. Второй опорный план

Рисунок №11. Второй опорный план и проверка целевой функции

.Подсчитаем число занятых клеток таблицы на рисунке №11.

Количество занятых клеток равно 6, а должно быть m + n - 1 = 6. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

(x) = 625

.Далее итерация повторяется до тех пор, пока все потенциалыне станут равны нулю, следовательно u_i + v_i≤c_ij, тогда предложенный план оптимален.

На рисунке №12 можно увидеть результат деятельности программы «АОС транспортная задача», который подтверждает, что изначально предложенный план по доставке и распределения груза оптимален, и поздравление с его получением.

Рисунок №12. Окончательный вариант плана поставок товара предоставленный программой «АОС транспортная задача»