Построение ПИД-регулятора

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ФАКУЛЬТЕТ

ПРИКЛАДНОЙ МАТЕМАТИКИ, ИНФОРМАТИКИ И МЕХАНИКИ

КАФЕДРА ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ И АВТОМАТИЧЕСКОГО

РЕГУЛИРОВАНИЯ

Контрольная работа

ТЕМА:

ПОСТРОЕНИЕ ПИД-РЕГУЛЯТОРА

Профессор, доктор

технических наук Лозгачев Г.И.

Научный руководитель Лозгачев Г.И.

Выполнил студент 4 курса в/о Анчаков П.Ю.

Воронеж 2013

Содержание

Введение

1. Постановка задачи

2. Построение передаточной функции

3. Построение области устойчивости

4. Подбор коэффициентов для определения наибольшей устойчивости системы

Выводы

Список использованных источников

Введение

Пропорционально-интегрально-дифференциальный (ПИД) регулятор - устройство в цепи обратной связи, используемое в системах автоматического управления для поддержания заданного значения измеряемого параметра.

ПИД-регулятор был изобретен в 1910 г.; позже, в 1942 г., Зиглер и Никольс разработали методику его настройки, а после появления микропроцессоров в 80-х годах развитие ПИД-регуляторов происходит нарастающими темпами.

ПИД-регулятор относится к наиболее распространенному типу регуляторов. Причиной столь высокой популярности является простота построения я промышленного использования, ясность функционирования, пригодность для решения большинства практических задач и низкая стоимость.

Основной задачей данной курсовой работы является практическое использование знаний, полученных в процессе изучения курса, развитие навыков в расчете областей устойчивости ПИД-регулятора и выборе оптимальных параметров регулирования.

Цель работы - построить область устойчивости и подобрать оптимальные параметры для заданного переходного процесса в системе MatLab.

1. Постановка задачи

Необходимо определить, как Y меняется во времени, то есть построить переходный процесс Y (t) - ? при Хз =

2. Построение передаточной функции

Запишем зависимость Y от Хз:

После преобразования получим:

Таким образом, передаточная функция имеет вид:

Рассмотрим знаменатель:

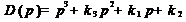
Знаменатель D (p) определяет устойчивость линейной системы.

3. Построение области устойчивости

Для определения устойчивости существует несколько критериев:

1) Критерий устойчивости Гурвица

Пусть дано характеристическое уравнение системы вида при а0 > 0.

Гурвиц предложил алгебраический критерий, который основан на построении специальных определителей характеристического уравнения (2), называемых определителями Гурвица. Они составляются по следующим правилам:

по главной диагонали выписывают все коэффициенты от а1 до аn в порядке возрастания индекса;

дополняют столбцы определителя вверх от диагонали коэффициентами с последовательно возрастающими, а вниз - с последовательно убывающими индексами;

на место коэффициентов, индексы которых больше n и меньше 0, ставят нули.

В соответствии с этими правилами, определитель Гурвица n-го порядка имеет вид:

регулятор устойчивость передаточная функция

Определители Гурвица более низкого порядка являются диагональными минорами Dn. Например, при n = 3

; ;

Поскольку в последнем столбце определителя Dn стоят нули, за исключением, то Критерий Гурвица формулируется следующим образом:

для того чтобы АСУ была устойчива необходимо и достаточно, чтобы все определители Гурвица были положительными, и при этом выполнялось условие a0>0.

2) Критерий устойчивости Рауса

Этот критерий представляет собой систему неравенств, составленных по особым правилам из коэффициентов характеристического уравнения замкнутой САУ.

Критерий Рауса требует несколько меньшего объема вычислений, чем критерий Гурвица и более удобен для программирования на ЭВМ. Для суждения об устойчивости системы по этому критерию необходимо составить таблицу Рауса.

Таблица Рауса

В первой строке таблицы записывают коэффициенты характеристического уравнения, имеющие четные индексы в порядке их возрастания. Во второй строке таблицы записывают коэффициенты с нечетными индексами в порядке их возрастания. В последующие строки вписывают коэффициенты, определяемые как

Условия устойчивости Рауса: Чтобы САУ была устойчивой необходимо и достаточно, чтобы все коэффициенты первого столбца таблицы Рауса имели один и тот же знак, то есть были положительными. Если не все коэффициенты первого столбца таблицы Рауса положительны, то есть САУ неустойчива, число правых корней характеристического уравнения равно числу перемен знака в первом столбце таблицы Рауса.

В данной работе, поскольку количество коэффициентов мало, удобнее использовать критерий устойчивости Гурвица.

Найдем область устойчивости по критерию Гурвица. Для этого составим из коэффициентов матрицу и потребуем, чтобы ее главные миноры были положительны.

k₃ > 0₁k₃ - k₂ > 0₂ (k₁k₃ - k₂) > 0

т.к. k₁k₃ - k₂ > 0, то в последнем неравенстве достаточно потребовать, чтобы k₂ > 0. В итоге имеем систему:

₃ > 0₂ > 0₁k₃ > k₂

Найдем область устойчивости сначала для двух коэффициентов k₂ и k₃:

Далее будем подбирать k₁ так, чтобы выполнялось неравенство k₁k₃ > k₂.

4. Подбор коэффициентов для определения наибольшей устойчивости системы

Для построения переходного процесса умножим передаточную функцию на Хз

получим

Возьмем для начала k₁ = 3 k₂ = 0,1 k₃ = 2

С помощью системы MatLab разложим нашу дробь на сумму простых дробей.

>> [R,S,K] = RESIDUE (c,d)=

.4998 - 0.3627i

.4998 + 0.3627i

.0004

.0000=

.9830 + 1.4024i

.9830 - 1.4024i

.0341

=

[]

Здесь R - вектор числителей нашей суммы дробей, S - корни полинома в знаменателе.

Теперь получаем оригинал по формуле

с помощью функции

>> y=R (1). * (exp (S (1). *t)) +R (2). * (exp (S (2). *t)) +R (3). * (exp (S (3). *t)) +R (4). * (exp (S (4). *t));

Затем выводим график функции:

>> plot (t,y)

В данном случае мы наблюдаем достаточно большое отклонение (около 0.3) и достаточно длительное (5 сек) время нормализации.

Попробуем увеличить k₂: k₁ = 3 k₂ = 1 k₃ = 2

Видим, что увеличилось отклонение (больше 0.3) и время (около 6 сек).

Увеличиваем остальные коэффициенты: k₁ = 9 k₂ = 1 k₃ = 11

Отклонение и время нормализации заметно уменьшились. Попробуем увеличить k₂₁ = 9 k₂ = 2 k₃ = 11

Снова наблюдаем улучшение по всем параметрам. Увеличиваем k₂ еще на 1.

₁ = 9 k₂ = 3 k₃ = 11

Заметных изменений нет. Значительно увеличиваем k₂

₁ = 9 k₂ = 9 k₃ = 11

Заметна потеря устойчивости. Для проверки еще увеличим k₂

₁ = 9 k₂ = 30 k₃ = 11

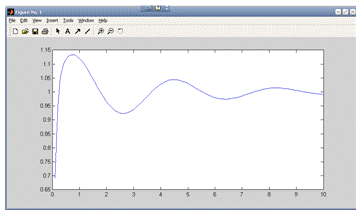
Видим, что k₂ увеличивать не стоит.

Попытаемся увеличить остальные коэффициенты

₁ = 17 k₂ = 1 k₃ = 15

Время стабилизации сократилось до 3-х, отклонение - до 0,05. Попробуем увеличить k₂

₁ = 17 k₂ = 2 k₃ = 15

Видим, что возросло отклонение. Уменьшаем k₂

₁ = 17 k₂ = 0,1 k₃ = 15

Отклонение и время уменьшились, увеличиваем коэффициенты

₁ = 30 k₂ = 1 k₃ = 30

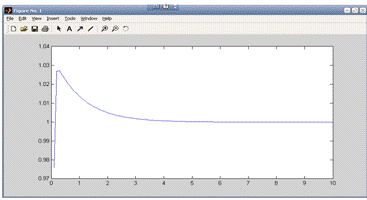
Отклонение стало меньше 0.03, что на данный момент является наилучшим результатом. Зная, что k₂ лучше уменьшать, уменьшим его

₁ = 30 k₂ = 0,1 k₃ = 30

Видим, что отклонение теперь составляет около 0.025, время - около 3.

Это наименьшие результаты, которых нам удалось достичь, поэтому будем считать, что при данных коэффициентах система наиболее устойчива.

Выводы

На примере был исследован ПИД-регулятор. Построена область устойчивости с помощью критерия Гурвица.

Математическая модель реальной системы не выбирается однозначно, это связано с тем, что существуют факторы, влияние которых можно проверить лишь экспериментально. Но она должна как можно полнее отражать свойства оригинала, и оставаться по возможности простой чтобы не усложнять исследования.

Исходя из структурной схемы, я построил передаточную функцию и определила область устойчивости системы.

Подбирая различные коэффициенты из области устойчивости, я выяснил, что система работает наиболее устойчиво при как можно меньшем k₂ и как можно больших k₁ и k₃. ь

Путем построения графика переходного процесса в системе MatLab мною было выяснено, что система наиболее устойчива при k₁ = 30 k₂ = 0,1 k₃ = 30.

2.      Теория автоматического управления. Том 1. Линейные системы.

.        Ким Д.П., Москва "ФизМатЛит - 2003"

4.      Попов Е.П. Теория линейных систем автоматического регулирования и управления: Учеб. пособие для втузов. - 2-е изд., перераб. и доп. - М.: Наука. Гл. ред. физ. - мат. лит., 1989. - 304 с.

5.      ПИД-регулятор [статья]: - . - (URL: http://ru. cybernetics. wikia.com/wiki/%D0%9F%D0%98%D0%94-%D1%80%D0%B5%D0%B3%D1%83%D0%BB%D1%8F%D1%82%D0%BE%D1%80) (дата обращения: 12.06.2012).