Развитие творческого мышления учащихся 5-6-х классов на уроках математики с помощью олимпиадных заданий

Развитие творческого мышления учащихся 5-6-х классов на уроках математики с помощью олимпиадных заданий

Содержание

Введение

Глава 1. Теоретические основы развития творческого мышления учащихся на уроках математики

.1 Психолого-педагогические аспекты мышления учащихся

.2 Виды и функции мышления

.3 Развитие творческого мышления решения олимпиадных задач

Вывод по 1 главе

Глава 2. Методические основы развития творческого мышления

.1 Использование типологии олимпиадных задач, развивающих творческое мышление учащихся 6-х классов на уроках математики

.2 Методические приемы работы с помощью учебных заданий на примере темы «Делимость чисел»

.3 Организация и результаты педагогического эксперимента

.4 Конспекты занятий

Конспект 3. Личная олимпиада

Конспект 4. Математическая регата

Конспект 5. Устная олимпиада

Вывод по 2 главе

Заключение

Список использованной литературы

Введение

Актуальность исследования. В современном информационном обществе, претерпевающем серьезные изменения во всех его сферах, востребуется самостоятельная творческая личность, обладающая системными знаниями и способная применять эти знания в практической деятельности. Решение глобальных проблем современности и разработка высоких информационных технологий возможны при наличии определенного стиля мышления, выводящего человека на осознание новых связей между объектами и обеспечивающего создание нового в духовной или материальной сфере. Такое мышление, направленное на создание чего-либо нового (идеального или материального), значимого для личности и общества, является творческим (М. Вертгеймер, И.Я. Лернер, Л. Секей, К. Тейлор, Е.П. Торренс, Веккер, Э.Г. Гельфман, Л.Э. Генденштейн, М.И. Махмутов, H.A. Менчинская, Э.Г. Мингазов, Д. Пойа, Г. Цумме и др.) вопрос рассматривается как особый и ведущий элемент обучения.

Однако анализ и обобщение практики изложения учебного материала по математике 6-х классов показывают, что проблема поиска дидактических возможностей учебного вопроса для развития творческого мышления в рамках учебной деятельности остается по-прежнему открытой. Таким образом, можно констатировать следующие противоречия:

• между значимостью проблемы развития творческого мышления учащихся и недостаточной разработанностью методических средств;

• между высокими развивающими возможностями заданий и недостаточной разработанностью научно-методических основ обучения математике 5-6-х классов с использованием разных типов заданий, ориентированных на развитие творческого мышления учащихся.

Объект исследования: процесс обучения математике учащихся 5-6-х классов.

Предмет исследования: развитие творческого мышления учащихся 5-6-х классов на уроках математики с помощью олимпиадных заданий.

Цель исследования: разработать и теоретически обосновать методику развития творческого мышления учащихся 5-6 классов на уроках математики при решении олимпиадных задач.

Для достижения цели исследования были поставлены следующие задачи:

. на основе анализа психолого-педагогической литературы выявить условия развития творческого мышления учащихся и критериев его сформированности;

. проанализировать существующие методические средства, способствующие развитию творческого мышления учащихся 5-6-х классов;

. выявить методические приемы работы с помощью учебных заданий на примере темы «Делимость чисел»

. определить мыслительную деятельность в процессе решения математических задач

  Глава 1. Теоретические основы развития творческого мышления учащихся на уроках математики

 

  1.1 Психолого-педагогические аспекты мышления учащихся

Фактически мышление явилось стержневой проблемой исследований (как теоретических, так и экспериментальных) в этой научной школе практически на всем протяжении ее самостоятельного существования. Выбор именно этой проблемы не случаен: мышление, выступавшее в качестве высшего проявления человеческого сознания, не получило сколь-нибудь удовлетворительного объяснения в традиционной, и гештальтпсихологи со всей присущей им решительностью приступили к исследованию продуктивного творческого мышления [11]. Объяснение этого сложнейшего проявления человеческого сознания должно было подтвердить справедливость претензий гештальтистов на создание подлинно научной.

Неверно было бы представлять дело так, что гештальтпсихология являлась единой теорией, основные положения которой разделялись бы всеми представителями данного направления. Вскоре после оформления гештальт как самостоятельного научного направления стали возникать разногласия, которые в дальнейшем значительно углубились, а отдельные представители этой школы (Макс Вертгеймер, Курт Коффка, Вольфганг Келер, Норман Майер, Лайош Секей и др.) зачастую оспаривали справедливость положений, выдвинутых коллегами. Существенно, что представления гештальтпсихологов о мышлении исторически претерпели серьезные изменения. Работы гештальтпсихологов неоднократно публиковались на русском языке, теоретические и экспериментальные исследования мышления в гештальт многократно анализировались в отечественной литературе, что избавляет от необходимости изложения концепций гештальтистов. Представляется особенно интересным зафиксировать комплекс исходных представлений о мышлении в гештальт и попытаться проследить хотя бы в самых общих чертах направление эволюции взглядов на мышление в этой научной школе.

В зарубежной психологии творческое мышление чаще связывают с термином «креативность». В 60-х годах XX в. толчком к выделению этого типа мышления послужили сведения об отсутствии связи между интеллектом и успешностью решения проблемных ситуаций. Было установлено, что последняя зависит от способности по-разному использовать данную в задачах информацию в быстром темпе. Такой тип мышления (Дж. Гилфорд, Н. Марш, Ф. Хеддон, Л. Кронбах, Е.П. Торренс) назвали креативностью и стали изучать ее независимо от интеллекта - как мышление, связанное с созданием или открытием чего-либо нового.

Для определения уровня креативности Дж. Гилфорд выделил 16 гипотетических интеллектуальных способностей, характеризующих креативность [34].

Среди них:

) беглость мысли - количество идей, возникающих в единицу времени;

) гибкость мысли - способность переключаться с одной идеи на другую;

) оригинальность - способность производить идеи, отличающиеся от общепринятых взглядов;

) любознательность - чувствительность к проблемам в окружающем мире;

) способность к разработке гипотезы;

) ирреальность - логическая независимость реакции от стимула;

) фантастичность - полная оторванность ответа от реальности при наличии логической связи между стимулом и реакцией;

) способность решать проблемы, то есть способность к анализу и синтезу;

) способность усовершенствовать объект, добавляя детали;

) и так далее.

Е.П. Торрес выделяет четыре основных параметра, характеризующих креативность:

легкость - быстрота выполнения текстовых заданий;

гибкость - число переключений с одного класса объектов на другой в ходе ответов;

оригинальность - минимальная частота данного ответа к однородной группе;

точность выполнения заданий.

Особый тип мышления, называемый в зарубежной психологии креативностью, в настоящее время широко изучается англо-американскими учеными, однако сущность этого свойства пока до конца не выяснена.

В отечественной психологии так же широко разрабатываются проблемы творческого мышления человека. Она ставится как проблема продуктивного мышления в отличии от репродуктивного. Психологи единодушны в признании того, что в любом мыслительном процессе сплетены продуктивные и репродуктивные компоненты. Большое внимание уделяется раскрытию сущности творческого мышления, выявлению механизмов творческой деятельности и природы творческого мышления.

И.Я. Лернер характеризует творческое мышление по его продукту. Учащиеся в процессе творчества создают субъективно новое, при этом проявляя свою индивидуальность[27].

С точки зрения Д.Б. Богоявленской, творчество является ситуативно нестимулированной активностью, проявляющейся в стремление выйти за пределы заданной проблемы.

По В.Н. Дружинину, творческое мышление - мышление, связанное с преобразованием знаний (сюда он относит воображение, фантазию, порождение гипотез и прочее).

Суть творческого мышления сводится, по Я.А. Пономареву, к интеллектуальной активности и чувственности (сензитивности) к побочным продуктам своей деятельности.

Я.А. Пономарев, В.Н. Дружинин, В.Н. Пушкин и другие отечественный психологи считают основным признаком мышления рассогласование цели (замысла, программы) и результата. Творческое мышление возникает в процессе осуществления, и связано с порождением «побочного продукта», который и является творческим результатом[9].

Выделяя признаки творческого акта, все исследователи подчеркивают его бессознательность, неконтролируемость волей и разумом, а также измененность состояния сознания.

Второй признак творческого мышления - спонтанность, внезапность творческого акта от внешних ситуативных причин.

Таким образом, главная особенность творческого мышления связана со спецификой протекания процесса в целостной психике как системе, порождающей активность индивида.

Иное дело - оценка продукта как творческого. Здесь в силу вступают социальные критерии: новизна, осмысленность, оригинальность и так далее.

С творческим мышлением сопряжены два личностных качества: интенсивность поисковой мотивации и чувственность к побочным образованиям, которые возникают при мыслительном процессе.

В качестве «ментальной единицы» измерения творческости мыслительного акта, «кванта» творчества, Я.А. Пономарев предлагает рассматривать разность уровней, доминирующих при постановке и решении задачи.

И.Я. Лернер считает, что основу творческого мышления представляют следующие черты: самостоятельный перенос знаний и умений в новую ситуацию; видение новых проблем в знакомых, стандартных условиях; видение новой функции знакомого объекта; видение структуры объекта, подлежащего изучению, то есть быстрый, подчас мгновенный охват частей, элементов объекта в их соотношении друг с другом; умение видеть альтернативу решение, альтернативу подхода у его поиску; умение комбинировать ранее способы решения проблемы в новый способ и умение создавать оригинальный способ решения при известности других [34].

Овладев этими чертами, можно развивать их до уровня, обусловленного природными задатками и усердием. Однако перечисленным чертам свойственна одна способность - «они не усваиваются в результате получения информации или показа действия, их нельзя передать иначе как включением в посильную деятельность, требующую проявления тех или иных творческих черт и тем самым эти черты формирующую».

Д.Б. Богоявленской была выделена (1983 г.) единица измерения творчества, названная «интеллектуальной инициативой». Она рассматривается как синтез умственных способностей и мотивационной структуры личности, проявляющихся в продолжении мыслительной деятельности за пределами требуемого, за пределами решения задачи, которая ставится перед человеком. Главную роль в детермининации творческого поведения играют мотивации, ценности, личностные черты. К числу основных черт относят: когнитивную одаренность, чувствительность к проблемам, независимость в неопределенных и сложных ситуациях.

В.А. Крутецкий структуру творческого мышления в математике представляет следующим образом:

способность к формализованному восприятию математического материала, схватывание формальной структуры задач;

способность к логическому мышлению в сфере количественных и качественных отношений, числовой и знаковой символики, способность мыслить математическими символами;

способность к совершенствованию процесса математических рассуждений и системы соответствующих действий, способность мыслить свернутыми структурами;

гибкость мыслительных процессов в математической деятельности;

стремление к ясности, простоте, экономичности и рациональности решения;

способность к быстрой и свободной перестройке направленности мыслительного процесса, переключение с прямого на обратный ход мысли;

математическая память (обобщенная память на математические отношения, типовые характеристики, схемы рассуждений и доказательств, методы решения задач и принципы перехода к ним);

математическая направленность ума.

Так же к творческому мышлению В.А. Крутецкий относит следующие «не существенные» компоненты: быстрота мыслительных процессов как временная характеристика; вычислительные способности; память на цифры, числа, формулы; способность к пространственным отношениям; способность наглядно представлять абстрактные математические отношения и зависимости.

Структура творческого мышления представлена в формуле: «математическая одаренность характеризуется обобщенным, свернутым и гибким мышлением в сфере математических отношений, числовой и знаковой символики и математическим складом ума».

Итак, в отечественной психологии исследования творческого мышления теоретически обоснованы, индивидуальные различия анализируются не только с количественной стороны, но и качественной стороны. Тем не менее, все еще незначительно количество исследований в этой области.

Таким образом, творческое мышление - мышление, связанное с созданием или открытием принципиально нового субъективного знания, с генерацией собственных оригинальных идей.

Показателем, характеризующим творческое мышление и на которые я буду основываться в своем исследовании следующее: беглость, гибкость и оригинальность мысли.

Беглость включает в себя два компонента: легкость мышления, то есть быстрота переключения текстовых заданий и точность выполнения задания.

Гибкость мыслительного процесса - это переключение с одной идеи на другую. Способность найти несколько различных путей решения одной и той же задачи.

Оригинальность - минимальная частота данного ответа к однородной группе.

В психологии развития существуют три подхода к проблеме развития творческого мышления:

) генетический, отводящий основную роль наследственности;

) средовой, представители которого считают решающим фактором развития внешние условия;

) генотип - средового взаимодействие, сторонники которого выделяют разные типы адаптации индивида к среде в зависимости от наследственных черт.

Мы в своей работе будем придерживаться 3 подхода, согласно которому развитие креативности идет по следующему механизму: на основе общей одаренности под влиянием микросреды и подражания формируется система мотивов и личностных свойств (нонконформизм, независимость, мотивация самоактуализации), и общая одаренность преобразуется в актуальную креативность.

Однако и в этом подходе существует несколько направлений. В.Н. Дружинин, В.И. Тютюнина и другие считают необходимым для развития творческого мышления:

отсутствие регламентации предметной активности, точнее - отсутствие образца, регламентированного поведения;

наличие позитивного образца творческого поведения;

создание условий для подражания творческому поведению и планированию проявлений агрессивного и деструктивного поведения;

социальное подавление творческого поведения.

Они выделяют между условиями и повседневной жизни индивида и достигнутым им уровнем творческого мышления. Идея эта по существу бихевиористская и заключается в том, что развитию творческого мышления способствуют те же аспекты ситуации, которые приводят к научению: повторение и подкрепление. А этап имитации является необходимым звеном развития творческой личности.

Дж. Вулвилл и Р. Лоу развитие творческого мышления не сводят к накоплению опыта, а представляют как структурное изменение операционного состава. Развитие (в рамках теории Ж. Пиаже) трактуется как возникновение уравновешенной структуры или уравновешивание (возникновение когнитивного конфликта). Творческое мышление развивается благодаря процессам, подобным «уравновешиванию» и запускаемым при возникновении когнитивного конфликта.

П.Я. Гальперин разработал развивающий метод, основанный на социальном взаимодействии. Идея социального научения (А. Бандура) заключается в том, что мы способны учиться, наблюдая поведение других людей и принимая его образец. Образцы творческого поведения могут передавать определенный подход к решению задач, к определению зоны поиска.

Таким образом, существуют два направления проблемы развития творческого мышления:

влияние условий воспитания и повседневной жизни;

проведение развивающего эксперимента.

Развитие совершается в процессе обучения и воспитания. Оно формируется в процессе взаимодействия с миром, посредством овладения в процессе обучения содержания материальной и духовной культуры, искусства. Поэтому есть возможность говорить о специальном, целенаправленном формировании творческого мышления, о системном формирующем воздействии.

Феноменологические традиции, методологические установки и основные оппозиции школы (в первую очередь В. Вундту, Вюрцбургской школе, О. Зельцу, формальной логике и бихевиоризму) обусловили исходные представления о мышлении. В основных чертах они могут быть сведены к следующему:

. Мышление есть продуктивный, творческий процесс.

. «Асубъектность» мышления, вытекающая из идеи феноменального поля (как протест против гипотетических тенденций, возникающих у субъекта и способных направлять процесс мышления), отказ от признания действия факторов «более высокого порядка» для объяснения избирательного и направленного характера мышления.

. Мышление есть трансформация, пере структурирование ситуации (в соответствии с феноменологической традицией мышление может быть раскрыто через его содержание).

. Переход от одного структурирования ситуации к другому (от одного гештальта к другому) достигается с помощью инсайда (противопоставление бихевиоризмам, утверждавшим в качестве основного способа постепенность решения задачи через пробы и ошибки).

. Ситуативность мышления и отрицание роли прошлого опыта (противопоставление ассоциативной Вюрцбургской школе и бихевиоризму).

. «Визуальность» мышления (влияние феноменологических традиций и предшествующих исследований восприятия, реакция на «безобразное» мышление и логицизм).

. Независимость мышления от культуры, невербальный характер мышления (традиции феноменологии, реакция на логицизм).

. «Сознательность» мышления, отрыв его от реального поведения, ограниченность сферой сознания (традиции феноменологии, вообще сознания).

. «Нерефлексивность» мышления - мышление есть принципиально одноуровневый процесс, совершающийся в мыслительном поле.

Итак, согласно исходным представлениям гештальтпсихологов, мышление рассматривалось исключительно с его содержательной стороны как переструктурирование ситуации путем инсайда, как переход от одного гештальта к другому.

Представления о мышлении в историческом развитии школы претерпели значительные изменения. Условно в эволюции гештальттеории мышления можно выделить три этапа:. «Классическая» гештальттеории мышления (работы М. Вертгеймера, К. Кофки, В. Келера и др., выполненные в 1920-х гг.).. «Неогештальттеория» мышления (исследования К. Дункера, Л. Секея, Н. Майера и др., посмертно опубликованная работа М. Вертгеймера «Продуктивное мышление», 1930-40-е гг.).. «Постгештальттеория» мышления (последующие работы Л. Секея, Н. Майера, А. Лачинса и др., 1950-70-е гг.).

Если на первом этапе большинство исходных характеристик мышления принимается, то на втором наблюдается отчетливый отход от целого ряда принципиальных положений. Третий этап вообще представляет собой попытки формирования «гибридных» теорий, синтеза с другими научными направлениями.

Если первый и второй этапы развития гештальтистских представлений о мышлении в отечественной литературе получили достаточно подробное освещение, то третий практически отражения не нашел. Поэтому остановимся на некоторых моментах, характеризующих второй и третий этапы.

Развитие гештальтпсихологической концепции мышления шло в направлении отказа от исходных ограничений и принятия положений, противоречащих первоначальным установкам:

) причины, обусловившие принятие тех или иных положений;

) изменение взглядов на методы, методики и стратегии исследования мышления.

Уже в работах К. Дункера [5; 6; 14] содержится отчетливое признание роли прошлого опыта в мышлении, решении задач (что, в частности, дало толчок для проведения целого цикла специальных исследований, направленных на изучение феномена функциональной фиксированности в решении мыслительных задач), находят отражение операционные и мотивационные характеристики мышления [5; 6].

Характеризуя книгу М. Вертгеймера [3], В.П. Зинченко отмечает, что «автор выходит за границы гештальттеории» [7, с.11], «Вертгеймер существенно трансформировал исходные понятия гештальт» [7, с.22], использует «непривычный для классической гештальт концептуальный аппарат, относящийся к описанию деятельности и действий. Здесь и понятия (или их аналоги) предметных значений или предметных обобщений, функциональных или операциональных значений, здесь есть и прототип описания функциональной структуры действий и даже ее модель, выраженная в абстрактных логических понятиях» [7, с.23].

Таким образом, работы второго этапа развития гештальттеории мышления сильно отличаются от исходных представлений об этом процессе. Остановимся на концепции Лайоша Секея, одного из наиболее интересных представителей гештальт, поскольку его работы (особенно последние) у нас малоизвестны. Первое исследование Л. Секея (1940) посвящено центральному моменту в решении задачи, который особенно интересовал гештальтпсихологов, - возникновению идеи. Секей отмечает, что важнейшим достижением современной мышления является признание того, что решение задачи состоит в пере структурировании материала [16, с.79]. Подход Л. Секея к исследованию мышления явно следует традиции, заложенной К. Дункером. Это следует специально подчеркнуть, так как представляется совершенно неоправданным мнение (основанное, вероятно, на обстоятельствах жизненного пути ученого), высказываемое некоторыми зарубежными историками, согласно которому Секея не считают принадлежащим к этой научной школе.

Секей, вслед за Дункером, полагает, что решение задачи представляет собой ряд последовательных фаз, которые закономерно вытекают одна из другой. Он выделяет (впервые описанные Дункером) эвристические приемы мышления - анализ ситуации и анализ цели, выявляет роль направления, которое принимает мышление (в зависимости от того, идет оно как анализ цели - «что мне нужно, чтобы достичь?» - или как анализ ситуации - «что нужно изменить в данном?») в решении (или нерешении) задачи. Важно отметить, что, по Секею, мышление не представляет собой «единообразного» во всех случаях процесса: пере структурирование мыслительного материала происходит не всегда; более того, эта переорганизация нужна в протекании не каждого мыслительного процесса. В этой работе Секея есть еще один крайне важный момент, ставящий проблему роли прошлого опыта в решении задач. «Окружающие нас предметы имеют определенное значение и ряд закрепленных за ними свойств» [16, с.87]. «За предметом в нашем понимании (на нашем уровне культуры, в нашем обществе) закреплены определенные функции, но в зависимости от специальных требований могут обнаруживаться новые свойства и возможности его применения. Обнаружение новых возможностей применения по-разному затруднительно в различных ситуациях. Это зависит от разных факторов, из которых только немногие известны сейчас» [16, с.88]. Для решения задачи часто необходимо обнаружить именно новое, неявное, латентное свойство предмета. Каким образом возможно обнаружение этого нового латентного свойства? По Секею, пере структурирование связано с бессознательным: «Этот вид пере структурирования… принадлежит, собственно, к арсеналу бессознательных и предсознательных механизмов» [16, с.94].

Отметим, что в цитированной статье имеются ссылки на публикации Фрейда, в частности на известную работу об остроумии и его отношении к бессознательному, имеющие, впрочем, чисто вспомогательное значение, но, как мы увидим, это обстоятельство оказывается важным для понимания логики развития концепции ученого.

Проанализируем основные положения этой работы в интересующем нас контексте.

Несомненно, что Секей исходит из традиций гештальт, непосредственно продолжая исследования К. Дункера. Исходное положение, согласно которому мышление - продуктивный процесс, представляющий собой пере структурирование, сохраняется [14]. Нопо остальным «позициям» происходит весьма радикальное изменение взглядов:

признается роль прошлого опыта, причем опыт не только является необходимым моментом в мышлении, но, в свою очередь, обусловлен культурой, общественным опытом;

признается роль действий субъекта (эвристические приемы, анализ ситуации, анализ цели);

мышление выступает как обслуживающее реальное поведение, является средством решения, в том числе, жизненных, практических задач;

происходит отказ от понятия феноменального поля (в работе речь идет о мысленных образах предметов, в которых должны выявляться новые свойства);

происходит отчетливое выделение различных уровней мыслительного процесса (осознаваемых и неосознаваемых).

Таким образом, можно видеть, что большинство выделенных исходных характеристик мышления оказались подвергнутыми пересмотру. В цикле последующих работ Секея (40-е - начало 50-х гг. XX в.) происходит разработка проблем, поставленных в первых экспериментальных исследованиях: соотношение знания и мышления, влияние способа обучения на возможности продуктивного применения, полученного знания и т. п. Это исследования, соответствующие второму этапу гештальттеории мышления.

На третьем этапе (1950-70-е гг.) теория мышления трансформируется за счет заимствования объясняющих понятий, выработанных в других научных школах. Л. Секей предпринимает попытку соединить традиции гештальт с положениями психоанализа и генетическими концепциями Жана Пиаже и Джерома Брунера. При этом сохраняется традиционная проблематика гештальт. Ставится задача объяснить пере структурирование мыслительного содержания, в результате которого достигается решение задачи. Наиболее интересной представляется работа Л. Секея «Творческая пауза» [15; 16], посвященная выяснению центрального момента в творческом мышлении - зарождения новой идеи, приводящей к открытию, нахождению решения задачи. Фактически эта работа выполнена на ту же тему, что и осаждавшаяся выше статья 1940 года. Эти исследования разделяет почти тридцать лет. Каковы основные отличия в понятийном аппарате и подходе к изучению мышления?

В последней статье Л. Секей в решении задачи различает следующие характеристики:

) содержание мышления,

) фазы (этапы) мышления,

) механизмы мышления, в которых различаются манипуляции и операции (абстракция, аналогия, обобщение, отрицание т.д.),

) уровни организации мышления (терпимость или нетерпимость к противоречиям, нереалистическим предположениям и т. п.)» [15, S. 142].

Таким образом, творческое мышление, не только включает действия операции субъекта, но представляет собой интимно-личностный процесс, непосредственно 70 г., излагаются результаты исследований процесса группового решения задач, что совершенно чуждо гештальтистских традициям в изучении мышления [18].

Изменения взглядов гештальтпсихологов процесс мышления закономерны. Будучи вначале своего развития «чистым» направлением, не признававшим влияния «посторонних «факторов, гештальтпсихология столкнулась существенными трудностями в объяснении избирательного и направленного течения мыслительного процесса. Собственный экспериментальный материал оказался значительно богаче исходных схем, что заставило вносить коррективы в концепции. Поворот к практике, в первую очередь к вопросам обучения, также обусловил изменение представлений о мышлении и его основных характеристиках.

Направление эволюции представлений о мышлении свидетельствует, на наш взгляд, о тенденции к стихийной интеграции: к использованию комплексных описаний, предполагающих заимствования и тесное «взаимодействие», кооперацию, коммуникацию с другими исследовательскими подходами. Эта стихийная интеграция приводит к тому, что психологическая концепция выходит за рамки научной школы. Это неизбежно, так как постижение психического во всей реальной сложности вступает в противоречие с узкими теоретическими установками. На наш взгляд, это один из путей развития психологического знания.

 

  1.2 Виды функций мышления

О творческом мышлении в первый раз заговорили древнейшие греки. Древнегреческий мыслитель Платон полагал, что мыслительные способности (нус) - это то, что выделяет человеческую душу от звериной. Мысль - надындивидуальное по натуре творческое начало, приобщающее человека к божественному миру. Философ противопоставил суждению мысль понятие разума, имеющего «земное» происхождение. Данный тип разума имел нетворческий, рационалистичный вид. Вследствие в немецкой классической философии и тот и другой типа разума были воссозданы сначала И. Кантом и потом В.Ф. Гегелем. Божественный по природе, креативный вид интеллекта стали называть интеллектом, а второй - рассудком.

Во 2-ой половине XIX в., когда случилось подразделение науки от философии, предметом исследования стал творческий интеллект. Изучения мышления сосредоточились вокруг основ рассуждения и умозаключения.

Только к началу 1930-х гг. эксперты снова обратились к вопросу творческого интеллекта. Одним из основных исследователей данного вида мышления был М. Вертгеймер, что, осуждая ассоцианистический путь, писал, что в случае если решение задачи «...достигается в итоге элементарного припоминания, автоматического повторения, что было заучено прежде, благодаря беспорядочному открытию в серии незрячих проб, то я бы не осмелился охарактеризовать такой процесс рациональным мышлением» [5]. Из числа наиболее значимых особенностей творческого мышления Вертгеймер назвал его адаптивность и структурность. Адаптивность обозначает, что творческие процессы ориентированы на усовершенствование условия, а структурность - то, что в ходе решения происходит исследование особенностей проблематичной ситуации и изменение многофункциональных значений отдельных компонентов условия в рамках целостной структуры. Кроме того Вертгеймер обратил внимание на то, что задачи, которые активизируют творческое понимание, должны быть «нетипичными», экзотическими для человека. Решающий творческую проблему должен посмотреть на обстановку по-новому, применяя тайные характеристики предметов, необычные связи, пытаясь передвинуть основы и способы решения из одной области в иную, порой весьма отдаленную.

Начиная с конца 1950-х гг. творческие процессы становятся предметом опытного исследования многочисленных специалистов (Дж. Гилфорд, Е.П. Торранс, Д.Б. Богоявленская, Я.А. Пономарев, Р. Стернберг и др.). Совершенствуются способы диагностики, систематизируются творческие задачи. В настоящее время для диагностики творческого мышления применяют задачи, отличающиеся по 3 основаниям: по числу условий, которые нужно принимать во внимание с целью достижения решения, по «материалу» и согласно выраженности 1-го из шагов творческого процесса [11]. Что касается главного основания выделения творческих задач, то в 1 полюсе стоят задачи, которые могут иметь только лишь одно ограничительное условие, в другом - имеющие обилие условий. Образцом задач с минимальным числом условий могут служить упражнения на формирование фантазии: нарисовать несуществующее животное, придумать как можно больше предметов, основой для которых стал бы круг и т.п. Образцом заданий с большим числом условий являются так называемые трудные ситуации, которые формулируются с точки зрения человека, которому необходимо что-либо предпринять [15]. В данных ситуациях нужно принимать во внимание не только лишь «внешние» обстоятельства, такие, как особенности окружающего пространства, времени, энергетические, финансовые и материальные ресурсы, причинно-следственные закономерности среди объектами и предметами, но и «внутренние» обстоятельства, заданные логикой воздействия Лица в этой ситуации. «Материал» творческого мышления может быть: двигательным, образным и мировоззренческим.

Под обучающими функциями будем понимать такие функции, которые направлены на формирование системы математического мышления, умений, навыков у обучающихся (как предусмотренных программой, так и расширяющих и углубляющих ее содержание) на различных этапах ее усвоения. Обучающие функции задач можно подразделить на функции общего характера, специального и конкретного характера. Под общими обучающими функциями понимаются такие функции, которые имеют место не только в ходе обучения математике, но и всем предметам естественно-математического цикла. Под специальными функциями понимаются функции общего характера, соотнесенные только к обучению математике [11].

Под конкретными функциями задач будем понимать частные виды специальных функций. Ограничимся одним примером. Формирование у учащихся некоторого понятия (на уровне представлений о нем) - обще обучающая функция; формирование представления о натуральном числе - специальная обучающая функция; формирование представления о числе нуль конкретная обучающая функция.

К числу общих обучающих функций мышления относятся:

) формирование у учащихся некоторого понятия (на уровне представлений о нем, на уровне его усвоения и на уровне закрепления);

) установление различных связей между понятиями (от рода к виду, внутри предметные и меж предметные связи и т.д.);

) формирование описания, определения понятия; подведение объекта под понятие;

) формирование ведущих идей, законов, суждений;

) установление различных связей между ведущими идеями, законами, суждениями; структурных соотношений между ними, иерархии;

) формирование основных видов умозаключений, способов и приемов их проведения;

) формирование ведущих умений и навыков, характерных для данного учебного предмета;

) формирование умений и навыков выражения мысли в речи и записи;

) формирование умений и навыков моделирования учебного материала (чертежи, графики и т.п.);

) формирование умений и навыков в обращении с приборами, инструментами, таблицами, с учебной и справочной литературой.

В процессе обучения математике, наряду с образовательными целями, должны реализовываться и определенные воспитательные цели. Известно, что обучение воспитывает, прежде всего, своим содержанием - фактами и их истолкованием [7].

Главное состоит в том, чтобы планомерно использовать изучаемый материал, сам процесс учения, и в частности процесс решения задач для воспитания у учащихся устойчивых взглядов и убеждений. Эта общая цель воспитания реализуется на уроках математики различными путями. Итак, под воспитывающими функциями задач будем понимать функции, которые направлены на формирование нравственных качеств учащихся. В отличие от обучающих функций задач их воспитывающие функции, на наш взгляд, можно подразделить лишь на функции общего и специального характера. К числу общих воспитывающих функций задач относятся:

) формирование у школьников высокой степени сознательности, чувства ответственности перед обществом, социальной активности, оптимизма и гуманистической направленности;

) воспитание у школьников чувства товарищества, взаимопомощи, творческой инициативы, дисциплинированности и организованности;

) эстетическое воспитание учащихся (формирование чувства прекрасного, вкуса к прекрасному, потребности, желания и способности преобразовать окружающий мир и строить человеческие отношения по законам красоты, стремление пополнить свой запас художественных и эстетических знаний и т.д.);

) воспитание положительного отношения школьника к учебной деятельности, развитие интереса к учебе, любознательности;

) формирование умений рационализировать свою учебную работу и приемы ее оформления; воспитание способности доводить любое учебное задание до конца; формирование критичности в оценке результатов своей работы, наряду с чувством уверенности в правильности ее выполнения.

Наконец, под развивающими функциями задач будем понимать такие их функции, которые направлены на развитие мышления учащихся, на формирование качеств, присущих научному мышлению, на овладение приемами эффективной умственной деятельности. Такие функции делятся на общие и конкретные. К специальным развивающим функциям математических задач могут быть отнесены, например, следующие:

) умение математизировать простейшие ситуации жизненного характера, усматривать математические закономерности в окружающем мире;

) умение предсказать (предположить существование того или иного факта или свойства, относящегося к математическим объектам с достаточной степенью правдоподобия);

) умение доказать или опровергнуть то или иное математическое положение дедуктивным путем;

) умение планировать поиск решения задачи, исключить из условия ненужные данные, дополнять недостающие, отбирать методы, средства и операции, необходимые для ее решения, умение осуществить проверку правильности решения;

) иметь четкое представление о логической структуре курса математики, о том, что абстрактный характер математики является основной причиной ее многочисленных приложений в других науках, в технике, в народном хозяйстве;

) умение формулировать определения математических понятий и умение соотнести то или иное понятие с данным определением;

) умение быстро и правильно проводить вычисления с привлечением простейших вычислительных средств для облегчения исчисления на соответствующем его этапе; умение создать на основе теоретических знаний удобную вычислительную ситуацию, осуществлять проверку и прикидку правильности вычислений;

) умение распознавать то или иное математическое понятие в различных ситуациях;

) умение проводить исследование в простейших учебных ситуациях.

В качестве примера общих специальных и конкретных развивающих функций задач рассмотрим следующую функцию. Развить способности учащихся к обобщению изученного - общая развивающая функция; развитие способности обобщить то или иное геометрическое понятие - специальная развивающая функция.

 

  1.3 Развитие творческого мышления решения олимпиадных задач

В настоящее время в сфере образования на первый план выходит проблема воспитания творческой личности, становление которой происходит во всевозможных условиях и видах деятельности. Вектор развития России отчётливо перекликается с главной идеей, лежащей в основе Образовательной системы «Школа 2100», - ориентированность на личность, формирование ученика как самостоятельно мыслящего человека. Придерживаясь этого направления, мы решили пойти дальше и, основываясь на системе воспитания творческой личности, разработали методику обучения школьников решению нестандартных (олимпиадных) задач.

Под «нестандартной задачей» мы понимаем задачу, заключающую в себе нечто оригинальное, творческое. «Олимпиадная задача» трактуется как определённое задание из какой-либо области знаний, данное учащимся для соревнования. Решение олимпиадных задач - это творчество, определяющееся самим процессом (результат решённой задачи не является социальной ценностью).

Для реализации этого творческого процесса учащийся должен овладеть аппаратом творческой деятельности. При воспитании творчества у школьников, прежде всего, следует обратить внимание на то, что основу в этом возрасте составляет создание одних элементов творчества и приведение других к виду, который должен соответствовать творчеству, а вовсе не компоновка элементов творчества в систему [11].

Вот почему чем большее число значимых элементов, составляющих процесс творчества, задействовано, тем быстрее будет достигнута цель.

Часто бывает так, что серьёзное увлечение математикой начинается с решения какой-либо понравившейся нестандартной задачи. Такая задача может встретиться на уроке в школе, на занятии математического кружка, в журнале или книге. Богатым источником таких задач служат различные олимпиады - от школьных, районных и городских до международных.

Решение олимпиадных задач обычно не требует знаний, выходящих за рамки школьной программы. Такие задачи, как правило, сформулированы так, что они не принадлежат ни к одному из стандартных типов задач школьного математического курса. Поэтому решение каждой такой задачи требует особого подхода, наличие способности к интенсивному творческому труду. Умение решать нестандартные задачи свидетельствует о глубоком владение математическим аппаратом и развитой культуре математического мышления, а владение предметом гораздо важнее, чем просто «чистые знания», которые всегда можно пополнить с помощью хороших справочников.

Ниже приведены ссылки на страницы сайта с задачами олимпиадного уровня. Задачи распределены по тематикам, но деление это условно - часто одна и та же задача может быть отнесена к различным рубрикам, поэтому имеет смысл не ограничиваться просмотром только одной. Каждая страница начинается с небольшого теоретического материала. Иногда это несколько предложений, иногда - неплохой справочник, на который стоит обратить внимание. По каждой теме предложено 10 задач с достаточно подробными решениями, иногда несколькими способами, и 5 задач без решений для самостоятельного разбора.

Ученики 6 классов наиболее перспективны для освоения основ творчества. В этом возрасте идёт речь не о систематизации творческих компонентов, а об их становлении. Стабильный возраст (8-12 лет) даёт возможность ученику приобрести научный тип мышления, который связан с выделением существенного в окружающем мире, способностью обоснования, оценивания, контролем своих действий, выбором того или иного действия.

В целом школа содействует бессистемному формированию и развитию творческих аспектов у школьников. Поэтому следует особо отметить, что более перспективно вести обучение творчеству в системе в связи с наличием всех факторов ученика и условий для его воспитания.

Творческое мышление можно характеризовать по следующим элементам:

признаки (развитое воображение, критичность мышления, аналитичность, широта категоризации, беглость, гибкость, оригинальность);

качества (открытость опыту, широта категоризации, аналитичность, беглость мышления, оригинальность);

и умения (способность экстраполировать, определять скрытый признак, анализировать, быстро переходить от одной категории к другой).

Умения при решении нестандартных задач школьников зависят от возраста ребёнка, а их развитие и формирование - от особенностей возраста

Исходя из степени развития аппарата творчества, проявляются качества, способствующие решению нестандартной задачи (анализировать, синтезировать, предвидеть). Возрастные видовые особенности ребёнка влияют на успешное формирование различных творческих качеств. Но для этого необходимо обратить внимание на следующие аспекты:

. Воспитывая качества творческого мышления, следует учитывать его структуру, включающую:

понятие, с его приёмами анализа, синтеза, абстрагирования, сравнения, обобщения;

суждение, содержащее аргументацию и доказательство;

умозаключение, предполагающее аналогию, дедукцию, индукцию.

. Ориентироваться надо на аспекты творческой деятельности, присущие компонентам структуры творческого мышления.

. Внимание уделять внутри возрастным особенностям (кризисном и стабильному возрасту). Так, для кризисного возраста рационально ориентироваться, в первую очередь, на сравнение, обобщение, аналогию и только затем на наиболее высшую ступень - анализ, синтез. В стабильном возрасте при развитии творческого мышления, когда от сформированности мыслительных операций зависит преобладание форм мышления, обучать мыслительным операциям следует в системе.

Специфика обучения решению нестандартных (олимпиадных) задач вытекает из возрастных особенностей школьников. Обучение детей кризисного возраста предполагает разбор каждого этапа решения нестандартных задач, когда проговаривается название, уточняется его суть, каждый этап разбирается на конкретной задаче, и в дальнейшем постоянно происходит его отработка. Дети стабильного возраста обучаются в системе, где придерживаются определённой последовательности творческой деятельности по решению нестандартных задач [37].

Основные аспекты, сопутствующие обучению решению нестандартных задач, включают ряд ключевых составляющих успеха, которые характерны для различных периодов школьного возраста и соотносятся с личностно, культурно, деятельностно ориентированными принципами. Сами принципы применимы не только к механизму усовершенствования аппарата творчества, необходимого для решения нестандартных (олимпиадных) задач, но и к классификации обучения решению нестандартных задач по изучаемым разделам математики. В результате процесс обучения обретает систему, которая даёт возможность не только активно использовать задачи по основным направлениям математического материала, но и в полной мере соответствовать особенностям данного возраста и индивидуальности каждого учащегося, что приводит к более действенным результатам.

  Вывод по 1 главе

Таким образом, специфика обучения решению нестандартных (олимпиадных) задач вытекает из возрастных особенностей школьников. Обучение детей кризисного возраста предполагает разбор каждого этапа решения нестандартных задач, когда проговаривается название, уточняется его суть, каждый этап разбирается на конкретной задаче, и в дальнейшем постоянно происходит его отработка. Дети стабильного возраста обучаются в системе, где придерживаются определённой последовательности творческой деятельности по решению нестандартных задач.

Основные аспекты, сопутствующие обучению решению нестандартных задач, включают ряд ключевых составляющих успеха, которые характерны для различных периодов школьного возраста и соотносятся с личностно, культурно, деятельностно ориентированными принципами. Сами принципы применимы не только к механизму усовершенствования аппарата творчества, необходимого для решения нестандартных (олимпиадных) задач, но и к классификации обучения решению нестандартных задач по изучаемым разделам математики. В результате процесс обучения обретает систему, которая даёт возможность не только активно использовать задачи по основным направлениям математического материала, но и в полной мере соответствовать особенностям данного возраста и индивидуальности каждого учащегося, что приводит к более действенным результатам

  Глава 2. Методические основы развития творческого мышления

 

  2.1 Использование типологии олимпиадных задач, развивающих творческое мышление учащихся 6-х классов на уроках математики

В соответствии с выделенными дидактическими возможностями олимпиадных задач, обеспечивающими эффективность процесса развития творческого мышления, нами была построена типология задач, в основу которой положено уровневое понимание учебного материала.

Система олимпиадных задач, которая основывается на уровневом понимании, может быть направлена на работу с понятиями, отрывком учебного текста или текста в целом. Для ученика задача будет тем труднее, и тем более приближенным к творческому уровню понимания, чем больший отрывок текста следует обобщить, чтобы ответить на него.

Остановимся подробнее на типах, способствующих развитию творческого мышления, приведем примеры из различных тем школьного курса математики 5-6-х классов.

К первому типу отнесем для ориентировки в информационном поле изучаемой проблемы. Результатом работы с ним является понимание того, какие факты нужны для получения решения.

Ответы на воспроизводящие олимпиадные задачи направлены на умения дать определения, найти факты, распознавать элементы информации, констатировать, перечислять, систематизировать, описывать, формулировать, приводить примеры, опираться на свои прошлые знания.

Первый уровень понимания предполагает опознание (идентификация) элементов информации; выявление фактов; использование ранее усвоенных математических понятий; словесное и визуальное описание объектов, которые обладают определенными свойствами.

Информацией для воспроизведения могут быть собственные знания и опыт учащегося. Информация может состоять из фактов, цифр, списков, таблиц, рисунков, словесного текста и т.д. учащиеся просматривает имеющуюся информацию, определяя ее достаточность для решения проблемы или определяя вид информации, которая может понадобиться для выбора оптимального решения.

Процесс понимания при ответе на учебный - усилия учащегося понять информацию поля задачи установить связи с предшествующей текстовой информацией, имеющимися знаниями

Примерами олимпиадных задач могут быть:

Задача 1

На кошачьей выставке в ряд сидит 10 котов и 19 кошек, причём рядом с любой кошкой сидит более толстый кот. Докажите, что рядом с любым котом сидит кошка, которая тоньше его.

Решение. Пусть каждая кошка укусит более толстого кота, сидящего рядом с ней, Любые 9 котов могли получить не более 18 укусов, значит каждый кот оказался укушенным, то есть рядом с ним сидит кошка, которая тоньше его.

Задача 2

Докажите, что если цифры десятизначного числа выписать в обратном порядке, то полученное число не будет в три раза больше исходного.

Решение. Предположим, что такое число нашлось. Его первая цифра может быть 1, 2 или 3 (потому что иначе в три раза большее число будет одиннадцатизначным).

Если первая цифра 1, то последняя - 7 (так как иначе при умножении на три на конце получится другое число - см. таблицу умножения на 3). Но тогда обращённое число получается более чем в три раза превосходит исходное.

Если первая цифра - 2 или 3, то последняя - 4 или 1, поэтому обращённое число получается слишком мало.

Задача 3

Есть 10 монет, среди них ровно две фальшивые. Детектор R7 за одну операцию исследует три монеты и указывает на одну из них. Известно, что детектор не может указать на настоящую монету, если среди тестируемых монет есть хотя бы одна фальшивая. Как за шесть тестов выявить обе фальшивые монеты?

Решение. Выберем три кучки по три монеты, протестируем каждую из них, и возьмём те три монет, на которые указал детектор. Среди них, очевидно есть хоть одна фальшивая. Протестируем эти монеты и таким образом определим одну из фальшивых. Вторая фальшивая монета может быть только среди тех четырёх монет, с которыми тестировалась найденная фальшивая или быть той монетой, которая ещё не была задействована. Среди этих пяти монет за два теста определить одну фальшивую уже совсем легко (каждый тест выявляет две настоящие монеты).

Задача 4

На доске написано пять двузначных натуральных чисел. Чебурашка каждую минуту прибавляет ко всем числам единицу или (тоже ко всем числам) двойку. После того, как Чебурашка увеличивает числа, К. Гена может стереть какое-нибудь число, делящееся на 13, или число, сумма цифр которого делится на 7 (если, конечно, такое число на доске есть). Докажите, что при любых действиях Чебурашки Гена через некоторое время сумеет стереть с доски все числа.

Решение. Гена может найти пять пар не более чем пятизначных соседних чисел, так, чтобы в каждой паре он мог стереть любое число. Чебурашка сможет «провести» через одну такую пару не более одного числа, а значит все пять чисел Гена сможет стереть.

Подобных пар очень много, например годятся пары 142 и 143, 312 и 313, 3120 и 3121, 1312 и 1313, 69999 и 70000

Ко второму уровню отнесем задачи, ответы на которые предполагают: понимание контекстной информации, которую можно додумать, реконструировать из учебного текста и контекста; выделение главного; установление связей между понятиями; объяснение причин; использование разных способов интерпретации фактов и явлений; обобщение математических понятий отношений и действий; соотнесение своих действий с целями собственной деятельности; готовность оценивать качество отдельных «шагов» собственной интеллектуальной деятельности и контролировать свои учебные действия.

Отвечая - объяснительный тип, учащиеся ориентируются на его формулировку, на слова, из которых он состоит, которые наводят их на ответ. Такие задачи необходимы на этапе актуализации прежних знаний, развертывания проблемы. К задачам этого уровня относятся следующие:

Задача 5

На одной стороне улицы разбитых фонарей стояло 150 фонарей, причём среди любых трёх фонарей, стоящих подряд, хотя бы один был разбит. После того, как электрик Петров починил несколько фонарей, среди любых четырёх фонарей, стоящих подряд, осталось не более одного разбитого. Докажите, что электрик починил не менее 25 фонарей.

Решение

способ. Разобьём фонари на 25 шестёрок подряд стоящих, и докажем, что в каждой из них был починенный фонарь. Предположим, что в какой-то шестёрке ни один фонарь не был починен. В такой шестёрке не менее двух разбитых фонарей (поскольку в каждой из двух троек, составляющих шестёрку, был разбитый фонарь), между которыми не менее трёх работающих фонарей (так как иначе можно будет указать четыре фонаря, среди которых хотя бы два разбитых). Но как раз трёх работающих фонарей подряд стоять и не может.

способ. Посмотрим на фонари до прихода электрика. В каждой тройке подряд стоящих фонарей есть хотя бы один испорченный, значит всего испорченных фонарей не менее 50. Пронумеруем первые 50 испорченных фонарей слева направо и разобьём на пары: 1-й со 2-м, 3-й с 4-м, и т.д. (всего 25 пар) Между фонарями одной пары все фонари целые, а значит их не более двух. Поэтому один из испорченных фонарей, входящих в одну пару, надо починить.

Задача 6

На Васиной чаше двухчашечных весов лежат гири весом 1 г, 3 г, …, 2001 г, а на Петиной чаше - 2 г, 4 г, …, 2000 г. Первым ходит Вася - он убирает по одной гире со своей чаши до тех пор, пока она не станет легче Петиной. Потом Петя убирает по одной гире со своей чаши до тех пор, пока она не станет легче Васиной. Затем опять ходит Вася, потом Петя, и так далее. Выигрывает тот, кто первым сможет убрать все гири со своей чаши. Кто выигрывает при правильной игре?

Решение. Выигрывает Вася. Ему достаточно до последнего момента не убирать со своей чаши гирю весом 2001 г.

В двух последних следует обратить внимание учащихся на то, что при ответе «может» достаточно привести хотя бы один подтверждающий пример (он фиксируется в тетрадях), тогда как ответ «не может» требует обоснований. Кроме фиксации примера, целесообразно задать учащимся дополнительный вопрос:

Рассуждения учащихся, проведенные таким образом, способствуют более глубокому пониманию математического содержания, создают возможности проводить рассуждения разными способами: с практической, геометрической, аналитической точек зрения последствий принимаемых решений.

Тип задач, направленных на третий уровень понимания назовем творческим.

Он основывается на реорганизации и трансформации имеющихся данных с тем, чтобы выйти за их пределы и увидеть изучаемый объект в новом виде. Очевидно, существуют два способа найти ответ: найти ответ в тексте, если достаточно хорошо знать текст и представлять, где нужно искать ответ на поставленный вопрос, однако учащемуся важно научиться искать и то, что он не знает.

Решение учащийся может дать различные ответы, находя различные способы их обоснования. Такие вопросы часто требуют обобщенного подхода к информации и расширенного ответа.

Задача 1: В правление фирмы входят 9 человек. Из своего состава правление должно выбрать президента и вице-президента. Сколькими способами это можно сделать?

Задача 2: Найдите пропущенное число:

13	60	17
16		14
26	20	14
19		31

Задача 3: Петя говорит: позавчера мне еще было 10 лет, а в следующем году мне исполнится 13. Может ли такое быть?

Задача 4: В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй - 20 суток и третий - 12 суток. Вернувшись в порт, теплоходы в этот день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем маршрутам. Через сколько суток они впервые снова вместе уйдут в плавание?

Задача 5: Немецкого учёного Карла Гаусса называли королём математиков. Однажды в школе (Гауссу тогда было 10 лет) учитель предложил классу сложить все числа от 1до 100. пока он диктовал задание, у Гаусса уже был готов ответ. Попробуйте догадаться, как Карл Гаусс складывал числа от 1 до 100 и запишите результат вычислений.

В рамках каждого уровня понимания можно выделить три типа задач, направленных на обогащение понятийного, рефлексивного и эмоционально-оценочного опыта. То есть на каждом уровне понимания - воспроизводящем, объяснительном и творческом - могут быть три разных типа.

На основании проведенного анализа текстов ряда учебников математики 6-х классов с точки зрения наличия в них учебных заданий разных типов, (п. 1.3), был выделен дефицит задач с использованием графики. Однако практика обучения творчеству требует активного применения графиков, рисунков, диаграмм и т.п., которые являются для ученика как бы инструментом обобщенного «видения» содержания новых абстрактных понятий и представлений.

Изобразительные и условно-графические средства (таблицы, схемы, рисунки, графики, диаграммы, репродукции картин, фотографии ученых и т.д.), являющиеся составными элементами учебных текстов, играют существенную роль в развитии творчества учащихся, обогащая их понятийный опыт. Сама по себе графическая наглядность еще не обусловливает развития творческого мышления учащихся. Для этого необходима тесная взаимосвязь процессов восприятия с процессами мышления. Чем содержательнее, активнее деятельность учащихся, связанная с графической наглядностью, тем эффективнее будет ее влияние на умственное развитие. Это позволяет говорить о том, что вопросы, сформулированные с помощью графической наглядности, могут обрести новую функцию - активизировать творческое мышление учащихся.

Познавательные задачи, применяемые для активизации творческого мышления учащихся, должны иметь свойство обобщенности. Такие вопросы позволяют акцентировать внимание учащихся на главном в изучаемом материале, подводят их к осмыслению той или иной закономерности, но не дают готовых выводов, а требуют определенной мыслительной активности, самостоятельности. Формы графической наглядности, которые не только дополняют словесную информацию вопроса, но и сами выступают носителями информации, способствуют обогащению понятийного опыта учащихся, необходимого для роста уровней понимания учебного материала.

Приведем примеры (рис. 2):

1. Каков замысел художника, нарисовавшего этот «портрет»?

психологический педагогический творческий математика

. Как вы думаете, что объединяет числа, украшающих «математическую» кошку?

. Как вы могли бы подписать этот рисунок?

. Какие бирочки можно поместить к представленным множествам натуральных чисел?

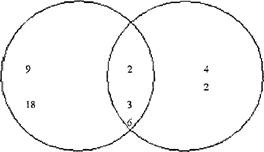
Такие типы задач можно отнести к творческим/понятийным. Следующие типы задач-заданий с помощью графической наглядности требуют самостоятельной постановки заданий и видоизменений условий. Цель таких задач-заданий - вызов ситуации, которая требует видоизменения решения. Речь идёт в этих случаях о выработке умений перестраивать известные способы решения в соответствии с изменением условий задачи. Успех этой перестройки непосредственно зависит от того, в какой мере учащиеся умеют анализировать задачи, улавливая одновременно и сходное, и различное. Это способствует обогащению понятийного опыта учащихся, выработке более сложных умений, которые необходимы для «восхождения» на высокие уровни понимания и, соответственно, для формирования творческого мышления учащихся. Примеры таких заданий представлены на рисунках (рис. 3,4).

Рис. 4. Вопросы-задания по рисунку Подобные задания развивают умения:

• ставить разумные вопросы, соотнося их постановку с графически представленному условию;

• математизировать ситуацию (т.е. переводить задачу с сюжета, заданного рисунком на язык математики);

• выбирать необходимые для решения величины из их чрезмерного множества или осуществлять вариативный поиск данных, недостающих для решения задачи;

• анализировать найденные решения, сравнивать их, выбирать подходящие, т.е. соответствующие здравому смыслу;

•        «разматематизировать» ситуацию (т.е. переводить полученный ответ на язык житейской практики).

•        Методический прием специального построения умозаключений делает процесс мышления учащихся более продуктивным. Учащимся необходимо между посылками и выводами восстановить необходимую зависимость, даже если эта зависимость скрыта неочевидными пропусками каких-то элементов операций мышления. Какие данные необходимы для решения поставленной проблемы? Какими способ можно решить проблему?

Результатом организованного процесса суждения может стать изменение, расширение, уточнение собственной точки зрения, что становится платформой для возникновения учебного сотрудничества, которое, в свою очередь, приводит к развитию познавательной и творческой деятельности.

Полученное графически систематизированное изображение решаемой проблемы является хорошей наглядной основой для самостоятельного ее осмысления. Оно дает возможность обдумать полноту и глубину изложения рассматриваемой в параграфе проблемы, выделить вопросы и взаимосвязи, нуждающиеся, с вашей точки зрения, в более полном раскрытии и обосновании и др.

Графическая организации текста с помощью заданий предполагает:

· оценку предмета изучения с точки зрения возможности выделения в нем больших и малых смысловых единиц;

· выделение смысловых блоков и более мелких единиц, графическое установление связей между ними;

· осмысление полученной графической систематизации текста (оценка полноты, обоснованности ответа, определение заданий, вызывающих сомнение, требующих более аргументированного изложения и т.д.);

· умение презентовать свою графическую схему текста.

Учебным вопросам, направленным на формирование и обогащение рефлексивного опыта учащихся, отводится значительное место, т.к. они обеспечивают реальную открытость учащегося новому опыту, окружающим его участникам учебного процесса, самому себе.

Психолого-педагогические исследования показывают, что осуществление рефлексии невозможно без саморазвития учащегося, без его «выхода» за пределы собственного опыта.

С помощью заданий, направленных на обогащение рефлексивного опыта, создается рефлексивная среда: в мышлении - проблемно - провокационных ситуаций; в деятельности - сотрудничество; в общении - открытость опыта для себя и других.

Психолого-педагогический анализ позволил выделить признаки заданий, направленных на развитие рефлексивного опыта в обеспечении развития творческого мышления учащихся:

. Признак сотворчества. Вопросы создают творческую позицию субъектов, взаимодействующих в учебном процессе. Этот признак выражается, во-первых, в критичности относительно чужого и своего опыта; во-вторых, в том, что ответ на вопрос - это не только результат, но прежде всего процесс совместного поиска.

2. Признак взаиморазвития. Он проявляется в том, что взаимодействие участников сотворчества связано не столько с взаимообменом опыта, сколько с взаимным преобразованием и достраиванием друг друга как целостных личностей. Каждый участник оказывается катализатором для развития другого.

3. Функциональный признак. Для субъектов сотворчества каждый новый опыт становится точкой отсчета, поводом для нового знания.

Создание выделенных рефлексивных признаков возможно с помощью организации заданий на обоснование позиции, идеи.

Такие учебные вопросы предполагают использование учащимися полученных навыков производить анализ информации, выносить оценочные суждения в нестандартных ситуациях. На этом этапе учитель дает возможность анализа учащимися конкретных учебных ситуаций. Такие задачи можно задавать и до, и после изучения темы.

1. Найдите число, которое записывается тремя различными цифрами, следующими в порядке возрастания, название которого состоит из слов, начинающихся с одной буквы. Ответ: 147

. Математики пишут учебник для второго класса. Какое наибольшее число различных примеров на сложение чисел 0, 1, 2, …, 8, 9 они смогут придумать? Ответ: 100

. Настя делилась с подругами конфетами, при этом она съела в три раза больше конфет, чем отдала. А её подруга Маша съела меньше всех, и число съеденных ею конфет было в восемь раз меньше, чем число конфет, съеденных остальными девочками. Скажите, со сколькими подругами Настя делилась конфетами, если конфеты были съедены все. Ответ: 2

. Школьники шли в музей парами. Оказалось, что пар из двух мальчиков в 3 раза больше, чем пар из двух девочек.Когда они шли обратно, пар из двух мальчиков было в 6 раз больше, чем пар из двух девочек. Можно ли построить детей так, чтобы пар из двух мальчиков было в 11 раз больше, чем пар из двух девочек?Если можно, укажите в ответе цифру 1, если нет - цифру 0.Ответ: 1

. На островах Туба, Юба, Руба, Муба и Коруба живут бабки Ёжки. К ним по морю приплыло 30 ступ. На каждом острове бабки Ёжки поделили ступы поровну. Причём оказалось, что у каждой бабки Ёжки на острове Туба ступ больше, чем у каждой бабки на Мубе; у каждой бабки на Мубе больше, чем у каждой на Рубе; у каждой на Рубе больше, чем у каждой на Мубе, и у каждой на Мубе больше, чем у каждой на Корубе. Определите, сколько бабок Ёжек живёт на Рубе, если на всех пяти островах бабок 20.Ответ: 1

. Переставьте две спички, и запишите в ответ полученное верное равенство.

Ответ: 2+3=5

. В таблице 3х3 расставлены положительные - как целые, так и дробные числа - числа. Произведения элементов в каждом строке и каждом столбце равны 1, произведение чисел в каждом квадрате 2х2 равно 2. Найдите число, стоящее в середине квадрата 3х3.Ответ: 16

. Решите кросснумбер и укажите в ответе время, на которое установлен будильник у Пети.

По горизонтали: 6 252- столько минут Петя может ещё спокойно проспать 7 2014- Петины часы сейчас показывают ровно столько часов

По вертикали:- квадрат целого числа- факториал какого-то числа

Пояснение: факториал числа n - произведение всех целых чисел от 1 до n, например: факториал числа 3 - это 1*2*3=6 11= 07- число, состоящее из одинаковых цифр 3

Ответ: 08:00

Данные задачи стимулируют обращение ученика к прошлому опыту и предполагают выдвижение гипотез. При ответе на подобные учебные вопросы, прямое усмотрение истины осуществляется единовременным обобщением без строгого логического доказательства. Такие вопросы развивают интуицию-догадку, которая необходима для развития творческого мышления.

Задачи, обогащающие эмоционально-оценочный опыт учащихся, дают возможность подумать о тех действиях, которыми они пользовались для решения проблем. Например, при изучении темы «О распределительном законе умножения относительно сложения», уместен вопрос о том, какой из предложенных способов представления закона в тексте им больше понравился и написать об этом в тетрадях.

Учащиеся могут представить различные способы представления этого закона: словесный, с помощью чисел, с помощью символов, с помощью рисунков.

К вопросам, обогащающим эмоционально-оценочный опыт можно отнести, например, такие вопросы:

· Какую часть суток вы спите, говорите по телефону, смотрите в окно?

· Какие задания вам показались более трудными?

·        Какие задания вам понравились?

· Ученик пропустил тему «Сложение целых чисел». Как бы вы ему рассказали, что -3+(+5)=2?

В данном параграфе рассмотрели использование разных типов задач и привели примеры их использования на примере основных тем курса математики 5-6-х классов.

Использование типологии, основанной на уровневом понимании учебного материала через обогащение понятийного, рефлексивного, эмоционально-оценочного опыта, способствует не только достижению учащимися обязательных результатов обучения и возможности углубленного изучения некоторых заданий учебного курса, но, кроме того, развивает умения анализировать, сравнивать, обобщать, планировать умственную деятельность, мыслить с учетом практического контекста, высказывать предположения, т.е. работать в творческом режиме.

 

  2.2 Методические приемы работы с помощью учебных заданий на примере темы «Делимость чисел»

Одной из основных содержательных линий школьного курса математики является линия изучения числовых систем, в частности, вопросы теории делимости целых чисел.

Проблемы, связанные с анализом свойств целых чисел, со всевозможными числовыми комбинациями, всегда привлекали внимание математиков, на всех ступенях человеческого знания играли большую роль. Например, работы П.Л. Чебышева демонстрируют возможности сочетания теории и практических задач, которые решаются различными математическими методами (задачи о губчатых колесах, о ветряных мельницах, о кройке платьев и т.д.). В теории чисел часто ставятся проблемы, которые просто и доступно формулируются, но поиски решения практических задач с использованием теории чисел создают условия для различных решений, поиска гипотез.

Тема «Делимость чисел», с одной стороны, имеет прикладное значение в курсе математики 6-х классов, т.к. теоретические и практические результаты, полученные при ее изучении, используются при выполнении преобразований рациональных чисел (поэтому успешность изучения данной темы сказывается на успешности изучения темы «Рациональные числа»). С другой стороны, данный учебный материал может создать условия для развития творческого мышления учащихся. Внешне простые по своей постановке задачи темы «Делимость чисел» привлекают учащихся, мотивируют их творческую деятельность. Изучая данную тему, школьники с необходимостью приобретают опыт поиска закономерностей построения гипотез, опровержения и обоснования соответствующих предложений.

Большинство задач по вопросам темы «Делимость чисел» отличаются по поиску их решений. Они формулируются на доступном для школьников уровне, не требуют для решения большой предварительной суммы знаний. Как правило, при их решении не требуется владение серьезными математическими техниками, что позволяет ученику с любым уровнем знаний активно включиться в учебно-познавательный процесс и максимально проявить себя. Задачи на делимость чисел входят не только в тематику олимпиадных заданий, но и в практику вступительных экзаменов в вузы.

Многие теоретико-числовые задачи школьного курса математики являются хорошей основой для самостоятельного планирования собственной деятельности: выдвигать цели и подцели, продумывать средства их реализации, выстраивать последовательность собственных действий и т.д.

Указанные особенности теоретико-числовых задач открывают богатые возможности их использования для развития творческого мышления учащихся, повышения качества знаний учащихся, развития у них устойчивого интереса к занятиям математикой.

Все вышесказанное определило выбор темы «Делимость чисел» в качестве примера организации работы с использованием типологии заданий, направленной на развитие творческого мышления учащихся.

Работа строилась с использованием учебной книги серии «МПИ» («Математика. Психология. Интеллект». «Делимость чисел» [35]).

Остановимся на содержании темы, которое создает условия ля постановки разных типов заданий.

В рамках данной темы учащиеся отвечают на один из заданий теории чисел:

«Делится ли одно целое число на другое?»

При ответе на этот вопрос создается широкий контекст, связанный с обсуждением выполнимости арифметической операции на различных числовых множествах. Вводится понятие «делитель натурального числа» и ставится задача поиска способов нахождения всех натуральных делителей данного натурального числа.

Учащиеся применяют свои знания о признаках делимости натурального числа; находят делители натуральных чисел, представляющих собой целое число сотен и тысяч; приходят к выводам о делимости произведения; обнаруживают новые признаки делимости; приходят к выводам о делимости суммы; учатся проводить доказательства некоторых признаков делимости. Наконец, рассмотрев разложение чисел на простые множители, получают способ нахождения всех делителей числа. Кроме того, учащиеся знакомятся с такими понятиями как «общий делитель натуральных чисел», «наибольший общий делитель натуральных чисел», «общее кратное двух натуральных чисел», «наименьшее общее кратное двух натуральных чисел». Учащиеся ищут закономерности, задают вопросы, проверяют их для различных частных случаев, предлагают контр примеры, обосновывают, учатся оформлять результаты своих исследований, рассуждать. В ходе этой деятельности учащиеся осознают смысл словесных выражений вида: «если... то», «тогда и только тогда», «те и только те», «неверно, что».

Работая над содержанием данной темы, школьники учатся отвечать на специальные типы заданий.

Осмысление познавательной ситуации начинается с понимания фактов (событий, явлений), которые носят констатирующий характер: субъект ограничивается узнаванием факта, актуализацией его смысла, сформированного в прошлой мыслительной деятельности, у учащегося «в уме» воссоздается та предметная ситуация, в которую включен требующий понимания факт. На это направлены вопросы воспроизводящего уровня понимания. Объяснительный уровень заданий требует более высокого уровня понимания и представляет собой процесс такого сопоставления с реальностью, в результате которого они, по мнению субъекта, «совпадают».

Работа по теме строилась специальным образом. Были составлены методические рекомендации для учителей, дидактические материалы для учащихся. Методические материалы для учителей включают развернутые цели изучения отдельных заданий темы, комплексы заданий для проведения уроков, вопросы для осуществления контроля, примеры различных форм проведения занятий, активизирующих деятельность учащихся при работе с вопросами и формирующих умения составлять вопросы. При составлении типологии заданий отмечаются особенности работы над понятиями.

Приведем примеры предлагаемых видов работы, способствующих развитию творческого мышления учащихся.

Пример 1. Вопросная карта изучения темы (рис. 6).

Рис. 6. Вопросная карта

Подобные вопросные карты позволяют учителю фиксировать признаки объекта, характеризующие понятия, что имеет большое значение для правильного использования понятий в учебной практике, дает возможность учителю охватить основные проблемы темы, посмотреть план ее изучения.

При изучении данного учебного материала необходимо акцентировать внимание учащегося на проблеме выполнимости операции на различных множествах, ввести понятие «делитель числа», постановке проблемы поиска натуральных делителей данного натурального числа.

Пример 2. Краткие советы по изучению темы «Делитель числа».

Таблица 4

Числовое множество	Всегда ли выполнима операция ?
	+	-	X
Натуральные числа	да	...	...
целые числа	да	...	да	нет

Вопросы, способствующие разно уровневому пониманию темы «Делитель числа» (табл. 4), могут быть представлены, например, таким образом:

Работа учеников с вопросом «Всегда ли выполнима операция?» позволяет отметить следующие моменты:

- аналогии между операциями сложения и умножения;

-        выполнимость арифметических операций на различных числовых множествах;

-        при работе с понятием «делитель числа»: а) дать определение; б) обоснование с помощью определения, что некоторое число является или не является делителем данного числа (например, что 2 - делитель числа 12, а 3 не является делителем числа 25);

-        в) проиллюстрировать, что если а: b, то и а: (-b);

-        дать понятие признака делимости.

Реализация возможностей типологии заданий по уровням понимания позволяет учащимся решать проблему, касающуюся темы «Делитель числа» постепенно, при этом создавая условия для активной познавательной деятельности учеников, развития их понимания учебного материала и, как следствие, развития творческого мышления.

задания, которые позволяют повторить ключевые моменты теории.

Приведем некоторые задачи-вопросы, которые предусматривают работу учащихся в рамках данной темы на разных уровнях понимания. Вопросы-задания воспроизводящего уровня понимания:

1. Какое число называется простым?

2. Может ли простое число быть а) четным; б) нечетным?

позволяют повторить ключевые моменты теории, акцентируя внимание на существенных особенностях определения простого числа, понятиях четного и нечетного числа.

. Известно, что целое число имеет делители 4, -3, 7. Какие делители, кроме данных, наверняка имеет это число?

Это вопрос объяснительного типа, ответ на который предполагает последовательность рассуждений учащихся:

Очевидным образом выписываются делители ±1, -4, 3 и -7. Если число делится на 4, 2, 7, это не означает, что оно делится на 8 или 56 (28:4, 28:2, но 28: 8). Ведь если число делится на 4, 2, 7, то его можно представить в виде произведения «4 - 7» или « 2 - 2 - 7», а вот дополнительного множителя 2 в этом произведении может и не оказаться, так как он уже содержался в множителе 4. То есть в данном случае можно точно определить делители ±1, ±2, ±7, ±4, ± 14 и ±28.

Подобные вопросы объяснительного типа требуют подробного описания процесса поиска, опровержения и подтверждения, дают возможность постепенного уточнения формулировок под влиянием дополнительно обнаруженных фактов, позволяют проводить аналогичные рассуждения на числовых примерах.

. Придумайте трехзначное число: а) не делящееся на 5; б) делящееся на 5, но не делящееся на 10 (сколько таких чисел?); в) делящееся на 10, но не делящееся на 5 (сколько таких чисел?).

Трехзначные числа, подходящие к условию пункта б) должны оканчиваться цифрой 5. Таких чисел, меньших тысячи, - 90 (по одному в каждом десятке каждой сотни, начиная со второй). Чисел, удовлетворяющих условию в), не существует ("а: 10 => а =...*** 0 => а: 5).

Этот вопрос закрепляет навыки использования признаков делимости и развивает комбинаторные умения учащихся.

Учитель предлагает учащимся выделить из предложенных им утверждений верные и неверные. Выполняя задание, учащиеся описывают заданную тему, обосновывая свой ответ. После знакомства с основной информацией (текст параграфа, лекция по данной теме) учитель возвращает учащихся к выделенным ранее группам «верные» и «неверные», и предлагает им оценить их первоначальный вариант, используя полученные на уроке сведения.

Данный методический приём можно использовать как для индивидуальной и групповой работы, так и для фронтальной на начальной стадии урока, когда идёт подведение к теме и актуализация знаний. Приём позволяет выяснить, что знают или думают ученики по обсуждаемому вопросу.

Пример 3. Комплексы заданий, основанные на уровневом понимании учебного текста через обогащение понятийного, рефлексивного и эмоционально-оценочного опыта учащихся, которые могут быть положены в основу проведения урока по определенной теме.

Как бы вы их объяснили? Каков вид слагаемых, на которые разбивается каждое число? Какова взаимосвязь между делимостью на 4 каждого слагаемого и делимостью на 4 их суммы? Каким свойством обладает делимость суммы?

Какое из чисел 24,25,26 можно поставить вместо * в сумму 2000+*, чтобы оно делилось на: с!. 4; е. 5.	Объяснительный/понятийный
Для того, чтобы обосновать, что число 372 делится на 4, один из учеников записал 372 = 300+72, а другой 372=360+12. Какая из записей помогает получить признак делимости на 4 любого натурального числа?	Творческий /рефлексивный
О какой разрядной единице мы можем твердо заявить, что она делится на 4?	Объяснительный/ рефлексивный
Как бы вы объяснили следующие записи: £ 43726; & |123456 ?	Творческий/понятийный
На карточке написано натуральное число, которое больше миллиарда. Какие цифры этого числа нужно знать, чтобы установить делится ли это число на: b. 2; 1. 4; 5; к. 8.	Творческий/понятийный
Сможете ли вы сформулировать признак делимости на 4?	Творческий/рефлексивный
Что нового вы узнали о делимости чисел? Что полезного вы узнали в это теме?	Творческий/эмоционально - оценочный
Какой план действий вы бы предположили при получении признака делимости на 8?	Творческий/ рефлексивный

С помощью этих заданий учащиеся смогут уточнить понятие «признаки делимости», ввести свойство делимости суммы и с его помощью обосновать признаки делимости на 4,5,8.

Данный комплекс заданий носит избыточный характер, чтобы дать возможность учителю организовывать диалог в зависимости от возникающих ситуаций.

Приведем пример:

К теме делимость чисел можно предложить задание: «Верно, или неверно»?

Представленные вопросы (воспроизводящие, объясняющие, творческие) имеют либо утвердительные ответы, либо отрицательные. Данные ответы обучающиеся помещают в таблицу:

Верно	Неверно

Ответы могут быть полными, либо краткими.

Примерами заданий могут быть такие:

• Если хотя бы одно слагаемое делится на некоторое число, то сумма делится на это число?

•        Если ни одно из слагаемых не делится на некоторое число, то сумма не делится на это число?

• Если каждое из слагаемых делится на некоторое число, то и вся сумма делится на это число?

• Если а делится на в, а в делится на с, то а делится на с?

• Есть числа, которые могут иметь только 2 делителя?

• Есть число, которое имеет только 1 делитель?

•        Если уменьшаемое делится на некоторое число, а вычитаемое нет, то разность на это число не делится?

• Значение выражения 2к может оканчиваться нечетной цифрой?

• Значение выражения 10к может оканчиваться еще какой-либо цифрой, кроме нуля?

•        Если ш-делитель числа п, то существует такое натуральное число к, что п=т*к?

• На данное натуральное число п делятся все числа, кратные п?

• Среди делителей данного числа найдется наименьшее и наибольшее число?

•        Среди кратных данного числа всегда найдется наименьшее, но нет наибольшего числа?

• По последней цифре числа можно узнать делится оно на 9 или нет?

• Если п- нечетное число, то п+2 - четное?

• Если одно число делится на другое, то НОК этих чисел равен большему числу?

Заметим, что учитель не дает прямых оценочных суждений в адрес своих учеников, помогая им самостоятельно вырабатывать подходы к содержательной оценке хода и результатов собственной познавательной деятельности. Для обучающихся становится значимым не только усваивать «правильное» знание, но и сомневаться, противопоставляя собеседнику другую точку зрения, другое мнение, иной подход к оценке.

В данном фрагменте урока деятельность учителя провоцирует учащихся к рефлексии. В рассматриваемом, фрагменте роль таких «провокаторов» играют вопросы учителя, обращенные к Ане и Лене:

Что дает вам этот ответ? Зачем вам этот вопрос?...

В данном параграфе представлены некоторые элементы методики использования типологии учебных заданий, способствующей развитию творческого мышления учащихся.

Представленные типы заданий создают условия самостоятельно переносить ранее усвоенные знания и умения в новую ситуацию; видеть проблемы в знакомой ситуации; видеть новые функции объекта; видеть проблемы; видеть альтернативы решения; комбинировать ранее усвоенные способы деятельности в новые, применительно к возникшей проблеме, строить субъективно новые способы решения (в отличие от других, известных), то есть научить учащихся творческим процедурам.

 

  2.3 Организация и результаты педагогического эксперимента

Педагогический эксперимент проходил в шестых классах Гимназии №2 г. Город, и состоял из трех этапов: констатирующего, поискового, формирующего. Охват обучаемых на поисковом этапе составил 62 человека; объем выборки на заключительном этапе формирующего эксперимента составил 40 человека.

Целью первого этапа эксперимента являлось выявление состояния проблемы развития творческого мышления учащихся 6-х классов на уроках математики, организации учебной деятельности, направленной на развитие творчества учащихся. Данный этап включал проведение пилотажных исследований, анкетирование и беседы с учителями. В частности, учащимся 6-х классов по основным темам курса математики 6-го классов предлагались специальные задания (на выбор), инициирующие их творческую деятельность.

Тип урока: урок практического применения знаний.

Цель урока: сформировать умение складывать и вычитать смешанные числа.

Задачи:

образовательные:

закрепить умение складывать и вычитать смешанные числа.

воспитательные:

вовлечь в активную деятельность всех учащихся класса;

создать условия для воспитания навыков сотрудничества;

воспитывать у учащихся любознательность и положительную мотивацию к учению.

развивающие:

развивать познавательный интерес и логическое мышление;

развивать навыки коллективной работы учащихся в сочетании с самостоятельной.

Форма работы: групповая форма работы.

Время реализации урока: 45 минут.

Учащиеся:

актуализируют:

понятия «сократить дробь», «смешанное число», «наименьший общий знаменатель», «целая часть», «дробная часть», «неправильная дробь»;

умение приводить дроби к наименьшему общему знаменателю;

умение складывать и вычитать дроби с разными знаменателями;

умение выделять целую часть из неправильной дроби;

умение сокращать дробь.

приобретут:

положительную мотивацию к обучению;

навыки коллективной работы.

закрепят:

умение складывать и вычитать смешанные числа.

Необходимое оборудование и материалы: компьютер, проектор, презентация урок-игра «Веселый садовник», названия групп («Зеленые», «Желтые», «Оранжевые» и «Красные»), томаты или красные кружки.

Дидактическое обеспечение урока:

Таблица «Действия со смешанными числами».

Сообщение «Томаты».

Дополнительная необходимая информация:

Предварительно класс необходимо поделить на четыре группы по трем уровням сложности: легкий уровень - группа «Зеленые», средний уровень - группа «Желтые» и группа «Оранжевые» и сложный уровень - группа «Красные».

Если класс слабый, то лучше, чтобы каждая группа решала примеры и уравнения своего уровня. Если класс сильный, то можно каждой группе дать возможность решить все задания, а затем проверить правильность их решения, нажав на соответствующую кнопку на слайде.

Ход урока

Мотивация учащихся. Здравствуйте, дети! Сегодня на уроке мы закрепим умение складывать и вычитать смешанные числа. Работать вы будете в четырех группах: «Зеленые», «Желтые», «Оранжевые» и «Красные».. Актуализация ранее изученного материала

. Проверка домашнего задания. Задание: сопоставьте ответ с номером домашнего задания.

. Тест.

Вопрос классу: о какой овощной культуре идет речь? Это одна из самых популярных овощных культур, хотя долгое время она считалась несъедобной и даже ядовитой. Ее родина - Южная Америка. Итальянцы называют ее «золотое яблоко». (Выслушиваются ответы учеников).

Чтобы узнать кто из вас был прав, решим тест.

При нажатии на правильный ответ, будет появляться часть рисунка.

Сообщение «Томаты».. Отработка умений и навыков

Итак, каждая из групп будет «выращивать» томаты. Если вы правильно решили задание, то ваша группа будет вознаграждена, получит томат.

У каждого ученика из группы должно быть решено задание в тетради.

Выполнение заданий по слайдам.

Физкультминутка (упражнение для глаз):

Закрыть глаза. Отдых 10-15 с. Открыть глаза. Повторить 2-3 раза.

Закрыть глаза. Выполнить круговые движения глазными яблоками с закрытыми глазами вправо и влево. Повторить 2-3 раза в каждую сторону.

Поморгать глазами. Повторить 5-6 раз.. Итог урока.

Учащимся, работающим у доски, в зависимости от количества «выращенных» его группой томатов, выставляется оценка.

Рефлексия деятельности на уроке: обсудить с учащимися урок, предложив учащимся продолжить фразу «Сегодня на уроке я…».

% учащихся не выбрали ни одного задания творческого характера, результаты выполнения выбранных заданий показали неумение учащимися актуализировать свои знания при решении новых задач, использовать общие методы и идеи, демонстрировать разнообразие и гибкость знаний.

Был проведен качественный анализ создаваемых текстов по следующим показателям:

1. Оригинальность идеи, способов изложения.

а) находчивость в соединении «несоединимых» элементов;

б) использование метафор.

2. Эмоциональность образов:

вызывает ли представленное задание интерес и эмоции у слушателя.

3. Разнообразие идей, ассоциаций:

разнообразие и количество используемых образов, ситуаций, действий,

многообразие их способов построения.

4. Умение увидеть проблему.

В таблице 6 представлены результаты анализа по выделенным показателям.

Таблица 6

Умение увидеть проблему	Разнообразие идей, ассоциаций	Оригинальность идей, способов изложения	Эмоциональность изложения
40%	10%	15%	6%

На данном этапе эксперимента были проанализированы некоторые учебники математики для 6-го класса по вопросным характеристикам, представленным в п. 1.3.

На основе анализа с помощью вопросных характеристик текстов, выделенных H.H. Сметанниковой, A.B. Хуторским, М.М. Поташником, вопросы на применение составляют в среднем 40% от общего числа заданий, представленных в текстах учебников, вопросы на субъектно-личностный опыт составляют лишь 7%, вопросы для направления мышления - 15%; вопросы с использованием графики - 10%.

Таким образом, содержание учебников не учитывает всех возможностей заданий.

На курсах повышения квалификации учителям была предложена анкета по использованию разных типов заданий в практике обучения.

По результатам анкетирования были выделены следующие наиболее часто задаваемые учителями группы заданий:

• репродуктивного типа;

• переключающие внимание учащихся;

•        апеллирующие к эмоциям учащихся.

Результаты констатирующего эксперимента позволили определить цель и задачи исследования.

Результаты этого этапа эксперимента обозначили проблему поиска дидактических средств, создающих условия для развития творческого мышления на уроках математики. С этой целью был проведен теоретический анализ философской, педагогической, психологической литературы по теме исследования, который позволил выделить учебный вопрос как одно из средств, создающих условия для развития творческого мышления учащихся.

Целью второго этапа эксперимента поисковый этап, была разработка типологии учебных заданий, способствующих развитию творческого мышления учащихся 6-х классов, выявление психолого-педагогических и методических условий организации обучения учащихся 6-х классов средствами использования типологий заданий, апробировалась и корректировалась методическая система обучения с помощью заданий. Основное внимание на данном этапе исследования уделялось тем изменениям, которые вносит внедрение типологии заданий в результаты учебной деятельности и развитие качеств творческого мышления учащихся. Эти изменения прослеживались с использованием тех же заданий, которые были выделены на констатирующем эксперименте. Положительная динамика полученных данных (таблица 7) позволила сделать вывод, что предложенная методика преподавания с использованием специальной типологии заданий создает условия для развития творческого мышления учащихся.

Таблица 7

Умение увидеть проблему	Разнообразие идей, ассоциаций	Оригинальность идей, способов изложения	Эмоциональность изложения
60%	30%	45%	35%

Целью третьего этапа была проверка эффективности внедрения методики обучения математике с помощью типологии заданий, в основе которой заложены психо-дидактические характеристики заданий: их ориентация на уровневое понимание учебного материала, обогащение рефлексивного и эмоционально-оценочного опыта, обрабатывались, анализировались и обобщались результаты исследования, определялись перспективы дальнейшей работы. На данном этапе была разработана процедура оценивания результативности применения предложенной методики, а также интерпретированы полученные значения.

С целью диагностики уровня развития качеств творческого мышления (до экспериментального обучения и после экспериментального обучения), были использованы тесты творческого мышления П. Торренса.

Оценка выполнения этих тестов включает следующие показатели:

) скорость, или беглость,- количество ответов в каждом субтесте;

) пластичность, или гибкость,- степень разнообразия ответов, оцениваемая по количеству категорий в ответах;

) оригинальность - редкость, нетривиальность идей.

Фигурные тесты состоят из трех субтестов, на выполнение которых отводится 30 мин (по 10 мин на каждый).

Задание « Нарисуй картинку» - тест, в котором испытуемый должен придумать оригинальную картину с использованием определенного элемента.

В инструкции подчеркивается необходимость придумать такой рисунок, который никто больше не сможет придумать (оригинальность. Художественный уровень исполнения рисунков во всех заданиях фигурных тестов не оценивается.

Задание «Незавершенные фигуры» Незаконченные фигуры вызывают стремление завершить их простейшим и легчайшим способом. Таким образом, чтобы создать оригинальный ответ, необходимо контролировать это стремление и тормозить его удовлетворение. Каждая законченная фигура (их всего 10) оценивается по оригинальности. Количество выполненных заданий определяет показатель беглости, а степень разнообразия ответов - гибкость мышления.

Задание «Повторяющиеся фигуры» сходно с предыдущим. В задании «Повторяющиеся фигуры» стимулируются все характеристики творческого мышления. Беглость стимулируется инструкцией придумать как можно больше предметов и картинок, гибкость - сделать их как можно более разнообразными, оригинальность - попытаться придумать такие рисунки, которые никто не смог бы придумать.

Анализ полученных результатов показал, что в экспериментальных группах показатели творческого мышления достоверно увеличились после проведенного обучения. За этот период изменения аналогичных показателей у учащихся контрольной группы были незначительными.

Такой критерий развития творческого мышления, как «рефлексивность», определялся по количеству правильных ответов на вопросы, носящих рефлексивный характер.

На этапе формирующего эксперимента было важно определить желание обучающихся использовать свой творческий потенциал для решения творческих заданий. Для этого нами был введен критерий, который показывает желание индивида использовать свой творческий потенциал и назовем этот критерий творческой инициативой.

Каждому учащемуся было предложено на выбор пять заданий из 10- ти, представляющих для него интерес. Пять заданий носят репродуктивный характер, пять заданий носят творческий характер. К творческим отнесем задания, которые позволяют найти решение несколькими способами, требуют новых способов решения, отличных от ранее рассмотренных, предусматривают применение знаний в новых, нестандартных ситуациях.

Задания для учащихся 5-го класса:

1. Выполнить действия:

21 х 23+ 3(213 -52)=

2. Измени число или знак действий в числовом выражении так, чтобы его значение стало равно 0:

21 х 23 + 3(213 - 52)=

3. Скорость пешехода 6 км/ч, он прошел путь за 3 часа, а велосипедист проехал тот же путь за 1 час. Какова скорость велосипедиста?

4. Измени условие 3-ей задачи так, чтобы она имела абсурдный ответ.

Результаты:

Группы	Высокий	Средний	Низкий
5 ЭТ.	4,5%	9,1%	86,4%
5. К.Г.	4,7%	9,5%	85,8%

5. Сравни:

2 км 2 дм и 2 км 20 см 1час 10 минут и 110 минут

6. Вместо (*) поставить такие цифры, чтобы между выражениями можно было поставить знак равенства:

7(*) + (93 + 71): 4 = 36 * (*) + (97 + 7): 4.

7. Сторона квадрата равна 4. Найдите площадь прямоугольника, если его ширина равна сторона квадрата, а длина в 2 раза больше.

8. Прочти задачу №3. Какие вопросы к задаче ты бы еще мог задать?

9. Два автомобиля выехали одновременно на встречу друг другу из пункта А в пункт Б со скоростями 100 км/ч и 120 км/ч. Через сколько часов они встретятся, если расстояние между пунктами 660 км.

10.    Прочти условие задачи №9. Какое слово из задачи нужно исключить, чтобы решение ее стало неопределенным.

Анализ выполнения заданий на определение уровня сформированности операций «творческая инициатива» показал следующие

Кроме того, в конце 6-го класса проведена диагностическая рейтинговая контрольная работа. Способность и желание учащихся использовать свой творческий потенциал оценивались по критерию «творческая инициатива», который определялся по количеству выбранных и правильно выполненных заданий, носящих творческий характер. К творческим отнесем задания, которые позволяют найти решение несколькими способами, требуют новых способов решения, отличных от ранее рассмотренных, предусматривают применение знаний в новых, нестандартных ситуациях.

По результатам этой же рейтинговой контрольной работы мы сравниваем результаты успеваемости учащихся контрольных и экспериментальных классов.

В работе 19 задач, и у каждой задачи свой «вес» - количество баллов, причитающихся за верное решение. Цель решающего - набрать (за время, отведенное на контрольную работу) как можно больше баллов.

Время, отводимое на выполнение контрольной работы - 60 мин.

Рейтинговая контрольная работа по теме «Делимость чисел» (учебник серии МПИ) [35, с.120].

Отец и сын решили измерить шагами расстояние между двумя деревьями, для чего прошли одновременно от одного дерева до другого. Длина шага отца - 70 см, сына- 56 см. Найдите расстояние между этими деревьями, если известно, что следы совпали в точности

Простым или составным числом является сумма четырех последовательных натуральных чисел? Если сумма - число составное, то назовите хотя бы два его нетривиальных делителя5

Сравнение уровня выполнения заданий диагностической контрольной работы отображено в таблице 7.

Таблица 8

Участники эксперимента	Количество учащихся, получивших соответствующую отметку
	«5»	«4»	«3»	«2»	Всего
Контрольная группа	40	90	62	10	202
Экспериментальная группа	72	109	17	3	201 '

Для оценки значимости полученных результатов был использован статистический метод обработки данных К. Пирсона х^г (^{а =} 0,05).

В нашем случае выборки (контрольный и экспериментальный классы) и члены каждой выборки независимы, сумма-объемов (количество учащихся во всех классах) больше 20, значения в каждой ячейке таблицы больше 5. Таким образом, выполняются условия применения критерия%².

Эксперимент показал, что использование на уроках математики типологии учебных заданий, основанной на уровневом понимании учебного материала и психо дидактических характеристики заданий: их ориентации на обогащение понятийного, рефлексивного и эмоционально-оценочного опыта учащихся, позволяет создать условия для повышения качества математической подготовки учащихся, развивает их творческое мышление.

Эксперимент показал, что использование на уроках математики в 5 - 6-х классах типологии учебных заданий, основанной на уровневом понимании учебного материала и псих дидактических характеристики заданий: их ориентации на обогащение понятийного, рефлексивного и эмоционально-оценочного опыта учащихся, позволяет создать условия для повышения качества математической подготовки учащихся, развивает их творческое мышление.

 

  2.4 Конспекты занятий

Конспект 1. «Признаки делимости на 3»

В рамках данной темы учителю необходимо ввести соответствующие признаки делимости, сформировать представление об универсальном способе получения признака делимости на произвольное число и систематизировать знания учащихся по изучаемой теме.

Перед тем, как перейти к изучению признака делимости на 3, желательно повторить, какой общий способ получения признака делимости был использован ранее: находили первую разрядную единицу, которая делилась на данное число, и представляли число в виде суммы целого числа этих разрядных единиц и остатка. Теперь имеет смысл применить эту процедуру для обнаружения признака делимости на 3. Обоснование признака достаточно провести не в общем виде, а на конкретном числовом примере - на трехзначном или четырехзначном числе.

Получить признак делимости на 9 учащиеся могут самостоятельно, повторяя на конкретном числовом примере такую же процедуру. Учитель. Начнем урок с математической разминки. Скажите, пожалуйста, делится ли сумма трех последовательных натуральных чисел на 3? Дима. Это можно проверить, взяв, например, числа 3, 4, 5. Их сумма равна 12, она делится на 3.

Ксения. Но, может быть, для других трех последовательных натуральных чисел так не получится. Лучше записать сумму любых трех последовательных натуральных чисел (пишет на доске).

п + (п+1) + (п+2)=3п + 3=3(п+1)

Учитель. Действительно ли 3(п+ 1) делится на 3?

Ученики (хором). Да.

Саша. Если хотя бы один из множителей делится на некоторое число, то произведение делится на это число.

Учитель. Хорошо. Вашему вниманию предлагается еще одно задание (указывает на доску). Можно ли, не производя сложения чисел 26, 32, 60, 93, 122, выяснить, делится ли их сумма на 3?

Филипп. Я думаю, что нельзя. Если каждое слагаемое не делится на данное число, то о делимости суммы ничего определенного сказать нельзя. Света. Надо сложить числа и посмотреть, будет ли делиться на 3 их сумма. (Пишет с комментариями)

+ 32 + 60 + 93 + 122 = 333 делится на 3, хотя не все слагаемые делятся на 3. Учитель. Действительно, теперь очевидно, что число 333 делится на 3. Но сразу увидеть, будет ли делиться на 3, например, число 147, трудно. Или, например, числа 3984, 214... делятся они на 3 или нет? Хорошо бы нам знать... (пауза).

Егор. Признак делимости на 3

Учитель. Давайте им и займемся (пишет на доске).

Признак делимости на 3. Ксения. Можно замечание? Света складывала все числа. Я отбросила те, которые на 3 точно делятся. Потом проверила сумму 26, 32 и 122. Получилось число 180. Оно делится на 3. Каждое слагаемое делится на 3, значит, и сумма делится на 3. Поэтому я думаю, что о делимости 147 на 3 тоже можно легко судить - 147=120 + 27. У меня получился признак делимости на 3.

Если число удается разбить на слагаемые, каждое из которых делится на 3, то и сумма разделится на 3. Учитель. Интересный признак!

Егор. Очень трудоемкий. Надо поискать такой, чтобы было сразу видно, чтобы посмотрел на число и понял...

Учитель. Какой же метод «розыска» признаков делимости может привести к успеху?

Юра. Нужно записать число в виде суммы разрядных слагаемых и искать разрядную единицу, которая нацело делилась бы на интересующее нас число. А затем использовать делимость суммы.

Учитель. Ну что же, давайте применим этот метод для числа 147. Записи делаем в тетрадях. Кто желает поработать у доски? Саша (пишет с комментариями на доске). 147 = 100 + 4 • 10 + 7 (думает)

нацело на 3 не делится, 100 нацело на 3 не делится. Учитель. А как делится?

Саша (пишет). 10:3 =3 (остаток 1). 100: 3 - 33 (остаток 1).

Учитель. Так что же, нет в числе 147 разрядных единиц, делящихся на 3 без остатка?

Саша. Нет

Учитель. Неужели метод потерпел крах при встрече с числом 3? (Замешательство детей. Слышны неуверенные голоса «да»). Учитель. Может, нам поможет этот листок?

Вы, конечно, понимаете, что это - подсказка. Я эту подсказку расположу на запасной доске. Кто не захочет ею воспользоваться - пожалуйста, ищите признак делимости на 3 самостоятельно.

Учитель. На что вы обратили внимание в первых четырех строчках записки? Оля. Разрядные единицы записаны в виде суммы числа, делящегося на 9 и остатка 1.

Учитель. А зачем появилась запись 9 * 1+1, затем 9*11 + 1 вместо 99+ 1? Оля. Чтобы 9 выделить. Учитель. Что дальше?

Ксения. Каждую разрядную единицу записывают с помощью первых четырех строк.

Юля. Потом пользуются распределительным законом. Учитель. Зачем же у него выделены некоторые числа?

Дима. Число содержит две тысячи, а не одну; пять сотен; 7 десятков и 4 единицы.

Филипп (торжественно, он сделал открытие!). Это же цифры числа 2547!

(По классу проносятся звуки ликования.) Учитель. И что же дальше делают?

(В это время работающие самостоятельно предлагают ответить на вопрос о признаке делимости на 3, но учитель просит их чуть-чуть подождать.) Саша. Холмс складывает числа, кратные девяти, и сумму цифр числа 2574, а затем использует распределительный и сочетательный законы.

Учитель. Давайте еще раз посмотрим на последнюю строчку записи. Делится ли число 2574 на 9? Ученики (хором). Да.

Оля. Первое слагаемое содержит множитель 9, оно обязательно разделится; второе слагаемое 18 тоже делится на 9, значит, сумма разделится на 9. Учитель. Так от чего же будет зависеть, разделится число на 9 или нет ? Максим. От первого слагаемого не будет, оно всегда кратно девяти, а вот от суммы цифр числа будет зависеть.

Учитель. Верно. Давайте сформулируем признак делимости на 9.

Ксения. Число будет делиться на 9, если сумма цифр в его записи разделится на 9.

Антон. Надо, Ксюша, продолжить в другую сторону. Если число не делится на 9, то и сумма его цифр не делится на 9.

Учитель. Говорят: число делится на 9тогда и только тогда, когда сумма его цифр делится на 9.

Учитель. Что удивило, обрадовало вас в том результате, который вы получили?

Наташа. Вопрос о делимости большого числа свелся к вопросу о делимости меньшего числа

Учитель. Как вы думаете, можно ли подобным образом найти признак делимости на 3?

Ученики (вразнобой). Да, наверное.

Учитель. Давайте попробуем. Каждый в своей тетради попробует найти признак делимости на 3, работая с числом 147 (мы его оставили на полпути). Дети самостоятельно делают записи в тетрадях, кто-то обращается к записям на задней доске. Я в это время разговариваю с теми, кто работал над признаком делимости на 3 самостоятельно. Выслушиваю их, предлагаю, в свою очередь, заняться признаком делимости на 9. Так проходит пять минут и... поднимаются руки, почти во всех детских глазах - удовольствие. Учитель. Получилось? Открыли признак делимости на 3? Кто сформулирует?

Сережа. Число делится на 3 тогда, когда сумма его цифр делится на 3. Антон. Можно, наверное, на 3 снова не доказывать. Если число делится на 9, то на 3 и подавно разделится. Я дома посмотрю.

Конспект 2. Координатная плоскость

Цели урока:

Образовательная.

Обеспечить систематизацию знаний умений и навыков построения точки по заданным координатам, определения координаты точки.

Формировать умение самостоятельно проверять усвоение материала.

Развивающая.

Формировать умения творческой деятельности учащихся

Развивать систематичность и последовательность мышления.

Воспитательная.

Формировать мировоззрение (правильные представления), связанные с природой математики и её объектов, практические потребности людей.

Воспитывать творческий подход к решению математических задач.

Ход урока.

. Организационный момент.

. Актуализация знаний.

«Собери» ответы на данные вопросы.

. Закрепление материала

Задание 1

Задание 2

Задание 3. (морской бой)

Задание 4

Следующее задание предлагается выполнить самостоятельно.

Текст задания и координаты точек демонстрируются на экране.

Назовите имя молодого графа из сказочной повести Джаннии Родари.

Построив координаты данных точек и последовательно соединив линиями точки, получите подсказку к ответу.

(-4;-2)

(-5;-2)

(-6;-3)

(-6;-5)

(-5;-6)

(-3;-6)

(-2;-5)

(-2;-3)

(-3;-2)

(-4;-2)

(-4;-1)

(1;4)

(-1;4)

(-3;6)

(-1;6)

(3;2)

(5;2)

(3;4)

(1;4)

(1;-2)

(0;-2)

(-1;-3)

(-1;-5)

(0;-6)

(2;-6)

(3;-5)

(3;-3)

(1;-2)

. Итог урока

Чем мы занимались на сегодняшнем уроке?

Какие задания понравились больше всего?

Что нового узнали вы сегодня на уроке?

. Домашнее задание

П.45

№1418;1420;повторение №1421(а)

  Конспект 3. Личная олимпиада

1. Витя сложил из карточек пример на сложение, а затем поменял местами две карточки. Какие карточки он переставил?

З 1 4 1 5 9 + 2 9 1 8 2 8 = 5 8 5 7 8 7

. У овец и кур вместе 36 голов и 100 ног. Сколько овец?

. Хозяин обещал работнику за 30 дней 9 рублей и кафтан. Через три дня работник уволился и получил кафтан. Сколько стоит кафтан?

. На какое наибольшее число частей можно разделить тремя разрезами: а) блин; б) булку?

. В бутылке, стакане, кувшине и банке налиты молоко, лимонад, квас и вода. Известно, что вода и молоко находятся не в бутылке, в банке - не лимонад и не вода, а сосуд с лимонадом стоит между кувшином и сосудом с квасом. Стакан стоит около банки и сосуда с молоком. Определите, где какая жидкость.

. Три подруги были в белом, красном и голубом платьях. Их туфли были тех же трех цветов. Только у Тани цвета платья и туфель совпадают. Валя была в белых туфлях. Ни платье, ни туфли Лиды не были красными. Определите цвет платья и туфель каждой из подруг.

. Три товарища - Владимир, Игорь и Сергей - окончили один и тот же педагогический институт и преподают математику, физику и литературу в школах Тулы, Рязани и Ярославля. Владимир работает не в Рязани, Игорь - не в Туле. Рязанец преподает не физику, Игорь - не математику, туляк преподает литературу. Какой предмет и в каком городе преподает каждый из друзей?

. Как из бочки с квасом налить ровно 3 л кваса, пользуясь пустыми девятилитровым ведром и пятилитровым бидоном?

  Конспект 4. Математическая регата

Задача 1

. В школе 30 классов и 1000 учеников. Докажите, что есть класс, в котором не менее 34 учеников.(2 балла)

. Можно ли отмерить 8 литров воды, находясь у реки и имея два ведра: одно вместимостью 15 литров, другое - вместимостью 16 литров? (2 балла)

. Найдите значение выражения (ВАРЕНЬЕ): (КАРЛСОН). (3 балла)

Задача 2

. В магазин привезли 25 ящиков с яблоками трех сортов, причем в каждом ящике лежали яблоки одного сорта. Найдутся ли 9 ящиков одного сорта? (2 балла)

. Один сапфир и три топаза ценней, чем изумруд, в три раза. А семь сапфиров и топаз его ценнее в восемь раз. Определить прошу я вас, сапфир ценнее иль топаз? (3 балла)

. Таня пошла покупать ручки и карандаши. На все деньги, которые у нее были, она могла купить 6 ручек. На те же деньги она могла купить 12 карандашей. Но она решила купить одинаковое количество ручек и карандашей. Сколько?(4 балла)

Задача 3

. В школе 400 учеников. Докажите, что хотя бы двое из них родились в один день года.(2 балла)

. Бутылка и стакан весят столько же, сколько кувшин. Бутылка весит столько же, сколько стакан и тарелка. Два кувшина весят столько же, сколько три тарелки. Сколько стаканов уравновешивают одну бутылку?(4 балла)

. Используя ровно пять раз цифру 5, представьте любое число от 0 до 10.(5 баллов)

Задача 4

. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?

. Двое по очереди ломают шоколадку 6х8. За ход разрешается сделать прямолинейный разлом любого из кусков вдоль углубления. Проигрывает тот, кто не сможет сделать ход. Кто выиграет?

. У Маши, Саши и Даши вместе 11 воздушных шариков. У Маши на 2 шарика меньше, чем у Даши, а у Саши на 1 шарик больше, чем у Даши. Сколько шариков у Даши?

. Семья ночью подошла к мосту. Папа может перейти его за 1 минуту, мама - за 2 минуты, малыш - за 5, а бабушка - за 10 минут. У них есть один фонарик. Мост выдерживает только двоих. Как им перейти мост за 17 минут? (Если переходят двое, то они идут с меньшей из скоростей. Двигаться по мосту без фонарика нельзя. Светить издали нельзя. Носить друг друга на руках нельзя. Кидать фонарик нельзя.)

. По контракту Гансу причиталось по 48 талеров за каждый отработанный день, а за каждый прогул взыскивались 12 талеров. Через 30 дней Ганс узнал, что ему ничего не причитается, но и он ничего не должен. Сколько дней он работал?

. Вовочка собрал в коробку жуков и пауков - всего 8 штук. Если всего в коробке 54 ноги, сколько там пауков? (У жука - 6 ног, а у паука - 8 ног).

. В коробке лежат 10 красных и 10 синих шариков. Продавец, не глядя, достает по одному шарику. Сколько шариков надо вытащить, чтобы среди вынутых из коробки шариков обязательно нашлись два шарика одного цвета?

  Конспект 5. Устная олимпиада

1. До царя дошла весть, что кто-то из трех богатырей убил Змея Горыныча. Приказал царь им явиться ко двору. Молвили богатыри:

Илья Муромец: Змея убил Добрыня Никитич.

Добрыня Никитич: Змея убил Алеша Попович.

Алеша Попович: Я убил Змея.

Известно, что только один богатырь сказал правду, а двое слукавили. Кто убил змея.

. На улице, став в кружок, беседуют четыре девочки: Аня, Валя, Галя и Надя. Девочка в зеленом платье (не Аня и не Валя) стоит между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом и Валей. Кто какое платье носит?

. Из числа 382818 вычеркните две цифры так, чтобы получилось наибольшее возможное число.

. Расставьте знаки арифметических действий и скобки, чтобы получились верные равенства:

а) 4 4 4 4=5; б) 4 4 4 4=17; в) 4 4 4 4=20; г) 4 4 4 4=32; д) 4 4 4 4=64.

. Разделите 7 полных, 7 пустых и 7 полупустых бочек меда между тремя купцами, чтобы всем досталось поровну и бочек, и меда. (Мед из бочки в бочку не переливать!)

. Продолжите последовательность чисел: 1, 11, 21, 1112, 3112, 211213, 312213, 212223, 114213, …

. Отлейте из цистерны 13 литров молока, пользуясь бидонами емкостью 17 и 5 литров.

. Решите ребус: КНИГА + КНИГА + КНИГА = НАУКА.

. Костя разложил в ряд 5 камешков на расстоянии 3 см один от другого. Каково расстояние от первого до последнего камушка?

. Мама положила на стол сливы и сказала детям, чтобы они вернувшись из школы, разделили их поровну. Первой из школы пришла Аня, взяла треть слив и ушла. Потом вернулся из школы Борис, взял треть оставшихся слив и ушел. Затем пришел Витя и взял 4 сливы - треть от числа слив, которые он увидел. Сколько слив оставила мама?

. Расставьте скобки, чтобы получилось верное равенство:

А) 3248:16 - 3∙315 - 156∙2=600

Б) 350 - 15∙104 - 1428:14=320

В) 1 - 2∙3 + 4 + 5∙6∙7 + 8∙9 = 1995.

. Сумма уменьшаемого, вычитаемого и разности равна 26. Найдите уменьшаемое.

. Турист проехал автобусом на 80 км больше, чем прошел пешком. Поездом он проехал на 120 км больше, чем автобусом. Какое расстояние он проехал автобусом, если поездом он преодолел в шесть раз большее расстояние, чем пешком?

. Найдите наибольшее натуральное число, а) все цифры которого различны, б) все цифры которого различны и которое делится на 4.

. Из числа 1829 вычеркните одну цифру так, чтобы получилось наименьшее возможное число.

. Задумано трехзначное число, у которого с любым из чисел 543, 142, 562 совпадает один из разрядов, а два других не совпадают. Какое число задумано?

 

  Вывод по 2 главе

Рассматривая возможности вопроса как отправного пункта мыслительного, процесса и как средства, стимулирующего творческое развитие обучающихся, мы представили типологии заданий, в основу которых легло условие «уровневого» понимания, реализующих ведущие идеи и принципы развития творческого мышления учащихся в одном из его вариантов.

Какая форма понимания возникает у субъекта в конкретной ситуации, обусловлено, прежде всего, тем, в какие объективные обстоятельства средствами вопроса, требующие понимания, попадает обучающийся и какую задачу он решает в этих обстоятельствах. Восхождение учащимся на соответствующий уровень понимания с помощью вопроса обусловлено актуализацией собственного опыта: как учащийся перерабатывает информацию при ответе на вопрос, как он использует свои знания, каким образом контролирует свою деятельность, почему именно так и об этом он думает. Типология заданий, учитывающая интеграцию всех уровней ментального опыта, позволит учащемуся выйти из логики текста, совместить ранее несовместимое и получить решение, не выводимое из предложенного текста - решение творческое. Таким образом, были выделены вопросы по уровням: о воспроизводящие; о объясняющие; о творческие.

Представлена методика их составления и дидактические возможности в развитии творческого мышления на уроках математики в 5-ом и 6-ом классах.

В этой же главе нами выделены типологии рефлексивных заданий, заданий графической наглядности, их дидактические возможности в развитии творческого мышления учащихся. Особо отмечены вопросы- предвосхищения и вопросы-провокация, показаны возможности организации дидактических игр с использованием заданий.

Во второй главе нами выявлены и описаны методические приемы использования представленных выше типологий заданий на примере темы «Делимость чисел».

При решении проблемы диагностики развития творческого мышления учащихся, мы выделили такие качества творческого мышления как гибкость мышления, беглость мышления, оригинальность мышления. Эти качества мышления оценены с помощью тестов П. Торренса и творческого задания которое мы назвали «Я в мире чисел».

Желание индивида использовать свой творческий потенциал, мы полагаем, является критерием его творческого развития. Этот критерий назвали творческой инициативой. По тому, какие задания выбирают учащиеся (творческого или репродуктивного характера), можно судить об их инициативе.

В качестве интегрального критерия развития качеств творческого мышления мы выделили способность учащихся отвечать на вопросы рефлексивного типа и их способность задавать вопросы этого типа.

Экспериментальная методическая система обучения математике с использованием возможностей представленных типологий заданий создает для учащихся условия для развития повышения качества усвоения математических знаний и обеспечивает развитие качеств творческого мышления

 

  Заключение

Данное исследование было посвящено проблеме развития творческого мышления учащихся.

Анализ психолого-педагогической литературы, анализ текстов учебников математики (на примере темы «Делимость чисел») и результаты анкетирования учителей математики показали, что в школьной практике преобладают вопросы репродуктивного характера, направленные на запоминание фактического материала, а не на развитие творческого мышления. Проблема использования учебных заданий как дидактического средства, создающего возможности для развития качеств творческого мышления при обучении математике, как показало изучение литературы и исследований по методике преподавания математики, разработана недостаточно.

На основании выделенных противоречий, анализа философской, психолого-педагогической литературы, а также в результате изучения опыта работы на уроках математики учащихся 6-х классов была сформулирована проблема исследования: как с помощью учебных заданий в преподавании математики в 6-х классах развивать творческое мышление учащихся, а V также поставлена цель исследования: теоретическое обоснование и разработка методики преподавания математики в 6-х классах с помощью учебных заданий, реализация которой обеспечивает условия для развития творческого мышления учащихся.

Была спроектирована методическая система обучения математике с использованием возможностей типологии заданий, способствующей развитию творческого мышления учащихся с учетом специфики предметного содержания курса математики 6-го классов, позволяющего разработать и реализовать типологию заданий, создающую условия для развития творческого мышления. В соответствии с этим выделены типы заданий с постепенным расширением поля ответов, направленные на уровневое понимание учебного содержания. Выделены вопросы, направленные на обогащение различных форм ментального опыта. В рамках каждого уровня понимания выделены три типа заданий, направленных на обогащение понятийного, рефлексивного и эмоционально-оценочного опыта.

В работе представлены методические приемы использования типологии заданий на примере темы «Делимость чисел» к основным понятиям темы и даны методические комментарии. Выделены методические приемы использования типологии заданий с помощью графического оформления, организации дидактических игр, приведены примеры уроков, реализующих возможности специфики и разнообразия заданий для стимулирования творческого развития учащихся и их активности в самостоятельной постановке заданий.

Все это дает основание считать, что поставленные задачи исследования решены.

Получены следующие результаты и выводы:

• Теоретически обоснованы условия развития творческого мышления учащихся в процессе обучения математике, в частности, сформулировано положение о возможности развития творческого мышления на основе уровневой организации процесса понимания учебного материала;

• Проанализирована роль заданий (с учетом их дидактических и психолого-педагогических функций) с точки зрения их влияния на уровень понимания учебного материала и, как следствие, на развитие творческого мышления учащихся в процессе изучения математики.

• Разработана типология учебных заданий, основанная на учете уровней понимания учебного материала и псих дидактических характеристиках заданий: их ориентации на обогащение понятийного, рефлексивного и эмоционально-оценочного опыта учащихся.

• Внедрена методика организации учебного процесса с использованием типологии заданий и комплекса приемов организации деятельности учащихся по использованию и конструированию заданий, способствующая повышению качества математической подготовки и развитию качеств творческого мышления: беглости, оригинальности, гибкости, инициативы и рефлексивности.

• Разработаны методические рекомендации для учителей математики 5-6-х классов по использованию учебных заданий как средства развития творческого мышления учащихся, а также дидактические материалы для учащихся 6-х классов по теме «Делимость чисел» на основе предложенной типологии учебных заданий.

Таким образом, можно констатировать актуальность и востребованность проведенного исследования, а также оценить перспективы дальнейшей разработки данной темы.

Разработанная методика использования типологии учебных заданий по теме «Делимость чисел» может быть распространена на другие темы школьного курса математики 5-6-х классов, служить ориентиром при подготовке учителей к проведению занятий, а также использоваться как средство диагностики развития творческого мышления учащихся.

  Библиография

1.   Зинченко, В.П. Вступительная статья / В.П. Зинченко // Продуктивное мышление / М. Вертгеймер. - М.: Прогресс, 1987. - С. 5-26.

2.      Мазилов, В.А. Интегративные тенденции в: гештальтпсихология и проблема целостности / В.А. Мазилов // Человеческий фактор: Социальный психолог. - 2005. - Вып. 1 (9). - С. 27-38.

.        Мазилов, В.А. Целостность и интеграция в: (Некоторые методологические проблемы психологического исследования) / В.А. Мазилов // Вестник интегративной: Журнал для психологов. - 2005. - Вып. 1 (3). - С. 38-40.

.        Тихомиров О.К. Психология мышления. М., 2005.Хекхаузен Х. Мотивация и деятельность. Т. 1. М., 1986.

.        Буркина В.А., Титова Е.И. Методика работы с аномальными задачами// Молодой ученый. 2014. №2 (61). С. 740-741.

.        Ермолаева Е.И. Систематизация математических знаний у студентов строительных специальностей в рамках модульного обучения// Наука и школа. 2008. №1. С. 33-37

.        Титова Е.И., Чапрасова А.В. Различные трактовки понятия «задача» и методика их решения// Молодой ученый. 2014. №6 (65). С. 760-762.

.        Александрова, Э.И. Математика. 3 класс (система Д.Б. Эльконина. В.В. Давыдова) [Текст] / Э.И. Александрова - М. Вита-Пресс - 2004. - 211с.

.        Бородина, И.Ф. Педагогические условия развития творческих способностей учащихся старших классов в процессе преподавания литературы: Автореф. дис... канд. пед. наук. - Чебоксары: 2004.- 19с.

.        Гельфман, Э.Г. Математика. 6 класс. Учебник. Часть 1. Делимость чисел [Текст] / Э.Г. Гельфман - М: Просвещение: 2005 - 128с.

.        Гурова, Л.Л. Психология мышления [Текст] / Л.Л. Гурова - М., 2005. - С.126 -137.

.        Далингер, В.А., Толпекина Н.В. Организация и содержание поисково- исследовательской деятельности учащихся по математике [Текст] / В.А. Далингер, Н.В. Толпекина - Омск, 2004 - 264 с.

.        Зверева Н.М. Практическая дидактика для учителя: Учебное пособие [Текст] / Н.М. Зверева - М.: Педагогическое общество России, 2001. - 256 е.;

.        Зимняя, H.A. Педагогическая психология [Текст] /: И.А Зимняя: Учебник для вузов. 2-е изд., доп., испр. и перераб. - М.: Логос, 2002. - 384 С.

.        Влияние театрализованной игры на развитие творческих способностей дошкольников Л.Х. Цеева, А.В. Ситкова - Научно-методический электронный журнал "КОНЦЕПТ", 2014

.        Общие подходы к решению творческих задач на основе изобретательских технологий Г.С. Альтшуллера В.В. Утёмов - Научно-методический электронный журнал "КОНЦЕПТ", 2014

.        Применение фондов эффектов и ресурсов системы для развития научно-технического творчества учащихся

.        В.В. Утёмов - Научно-методический электронный журнал "КОНЦЕПТ", 2013

.        Этапы педагогической поддержки развития творческой одаренности младших школьников

.        И.И. Дереча - Научно-методический электронный журнал "КОНЦЕПТ", 2013

.        .Грецов А.Г. Тренинг креативности. Питер, 2008. - 202 с.

.        Мамедяров Д.М. Развитие творческого мышления старшеклассников на факультативных занятиях по математике (на основе фреймовой формы обучения): Диссертация кандидата педагогических наук // Махачкала, 2010 - 177 с.

.        Мамедяров Д.М. Вакилов Ш.М. Составление задач как способ развития творческого мышления // Сборник научно-методических статей: Проблемы преподавания математики и информатики в школе и ВУЗе. Материалы конференции 19-21 сентября 2008 г. Махачкала, 2008. - 228 с.

.        Шарифзода Ф., Миралиев А. Общая и профессиональная педагогика. Душанбе. Ирфон, 2013. с. 196

.        Ахмадов М.С. Подготовка будущего учителя начальных классов к формированию творческой ориентации учащихся в условиях осуществления межпредметных связей, //автореферат на соискание уч. ст. канд. пед. наук. Душанбе, 2012.- с. 12

.        Рахманова Д.З. Развитие творческих способностей будущих учителей начальных классов в процессе педагогической практики. // Журнал «Учёные записки» №3 (31), 2012.- с. 115

.        Шарифзода Ф. Педагогика интеграции. Душанбе. Ирфон, 2011.- с. 397

.        Концепция модернизации российского образования на период до 2010 г.: Утверждена распоряжением Правительства РФ от 29.12.2001 г. №1756-Р(п-2). М.: AKADEMIA АПК и ПРО, 2002. - 24с.

.        Амелюшкина С.М. Педагогические условия развития творческого потенциала младшего школьника в учреждении дополнительного образования: автореф. дис. канд. пед. наук: 13.00.01.- Москва, 2011.- 23с.

.        Капитонова, Т.А. Методика и технология профильного обучения математике Текст.: учеб.-метод, пособие / Т.А. Капитонова. Саратов: [б. и.], 2012.-115 с

.        Орлова, О.В. Исследование стремлений к творчеству: личностный подход Текст. / О.В. Орлова // Молодой ученый. 2011. - №12, т. 2. - С. 124-127.

.        Новоселов, С.А. Развитие творческих способностей учащихся в процессе математического моделирования проблемных ситуаций естественнонаучного содержания / С.А. Новоселов, В.П. Кочнев // Педагогическое образование в России. 2011.-№3.-С. 139-146.

.        Просвирова, И.Г. Структурно-содержательный и мотивационный аспекты формирования математических понятий у учащихся 6 классов Текст: дис.. канд. пед. наук: 13.00.02 / И.Г. Просвирова; Том. гос. пед. ун-т. Москва, 2010. - 171 с.

.        Садыкова, А.А. Методика подготовки будущих учителей математики к использованию моделирования в обучении школьников Текст: автореф. дис.. канд. пед. наук: 13.00.02 / А.А. Садыкова; Чуваш, гос. ун-т. Чебоксары, 2010.-26 с.

.        Качуровская, E.H. Формирование мотивации учащихся 6 классов к учебно-познавательной деятельности в процессе обучения математике Текст: дис. канд. пед. наук: 13.00.02 / E.H. Качуровская; Урал. гос. пед. ун-т. Екатеринбург, 2010. - 233 с.

.        Гузеев, В.В. Групповая учебная деятельность в образовательном процессе Текст. / В.В. Гузеев // Педагогические технологии. 2009. - №6. - С. 3-32.

.        Андреев, В.И. Педагогика творческого саморазвития Текст.: инновац. курс: учеб. пособие для студентов / В.И. Андреев. Казань: Изд-во Казан. ун-та, 2008.- 127 с.

.        Безусова, Т.А. Некорректные задачи как средство развития культуры математического и естественнонаучного мышления школьников Текст: дис. канд. пед. наук: 13.00.01 / Т.А. Безусова; Тюмен. гос. ун-т. Пермь, 2008. - 228 с.

.        Величко, Е.В. Обучаясь лечусь Текст.: реабилитац. программа по изобразит. деятельности в специализиров. Домах ребенка / Е.В. Величко. - Астрахань: АИПКП, 2008. - 128 с.

.        Дрязгунов, К.В. Формирование дивергентного мышления учителей в системе повышения квалификации Текст: автореф. дис. канд. психол. наук: 19.00.03 / К.В. Дрязгунов; Калуж. гос. пед. ун-т им. К.Э. Циолковского. - Калуга, 2002. 22 с.