Модель росту популяцій Ферхюльста
ЗМІСТ
ВСТУП
. АНАЛІТИЧНЕ ДОСЛІДЖЕННЯ Моделі
росту популяцій Ферхюльста
.1 Початкові дані
.2 Особливі точки
.3 Дослідження моделі на основі
характеристичного рівняння
.4 Умови стійкості
.5 Фазовий портрет особливої точки
. ЧИСЕЛЬНЕ МОДЕЛЮВАННЯ ПОВЕДІНКИ СИСТЕМИ
ПРИ РІЗНИХ ЗНАЧЕННЯХ ПАРАМЕТРІВ
.1 Випадок лінеаризованої системи
.2 Випадок нелінійної системи
.3 Економічна інтерпретація
отриманих результатів дослідження
ВИСНОВОК
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
ВСТУП
В даній курсовій роботі була модель росту популяцій
Ферхюльста.
Метою даної роботи є застосування теорії дослідження
динамічних систем в дослідженні моделі економічної динаміки.
Об’єктом дослідження в курсовій роботі є динамічне
середовище, що описує модель в розрізі зміни чисельності населення.
Предметом виступає модель росту популяцій Ферхюльста.
Виходячи з мети були поставлені наступні завдання:
– знайти особливі точки системи;
– визначити тип та стійкість особливих точок;
– зробити необхідні розрахунки та побудувати фазові
портрети;
– перевірити правильність результатів дослідження
числовим моделюванням;
– прокоментувати результати аналізу з точки зору
реальної економіки.
1. АНАЛІТИЧНЕ ДОСЛІДЖЕННЯ Моделі росту
популяцій Ферхюльста
1.1
Початкові дані
Дано систему рівнянь:
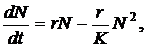
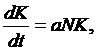 (1.1)
(1.1)
де
N - чисельність населення Землі;
K -
рівень технологічного розвитку;
r
- швидкість
росту чисельності населення;
rN
- додаток, що дає інформацію про необмежений ріст
населення;
 - негативний вплив взаємодії населення на
швидкість росту чисельності;
- негативний вплив взаємодії населення на
швидкість росту чисельності;
r>0.
1.2
Особливі точки
Система, що досліджується складається з двох диференційних
рівнянь і відповідно двох невідомих- чисельність населення Землі та рівень технологічного
розвитку. Також система
включає в себе два інших параметрів, які можуть приймати різні значення. Тому
проведемо теоретичне моделювання з оглядом всіх можливих станів системи і
визначенням умов її стійкості.
Для знаходження точок рівноваги системи необхідно прирівняти похідні 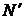 та
та 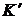 до нуля. Отримаємо (1.2):
до нуля. Отримаємо (1.2):
 (1.2)
(1.2)

 (1.3)
(1.3)

Звідси слідує, що N=0, K - будь-яке
число.
З першого рівняння маємо перший випадок:
 (1.4)
(1.4)
Відповідно К може приймати будь-які значення.
Другий випадок:
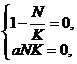 (1.5)
(1.5)
 (1.6)
(1.6)
 (1.7)
(1.7)
Отже, у досліджуваній системі у першому випадку при N=0 ми маємо рівноважну точку з координатами
(0;0), у другому випадку, коли bK-N=0 ми маємо пряму, що лежить на осі Оу,
при цьому К може набувати будь-яких значень. При цьому особлива точка
(0;0) задовольняє рівняння bK-N=0,
а отже лежить на даній прямій. Тому в подальшому будемо досліджувати дану
особливу точку.
1.3 Дослідження
моделі на основі характеристичного рівняння
Для подальшого дослідження моделі проведемо її лінеаризацію.
Відповідно отримаємо систему:
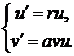 (1.8)
(1.8)
Знаходимо матрицю Якобі отриманої системи, як частинні похідні по u
та v:
 (1.9)
(1.9)
Підставляючи координати особливої точки (0;0) в матрицю 1.9 маємо:
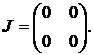 (1.10)
(1.10)
У нашому випадку det=0, отже
система має пряму точок рівноваги.
Складемо характеристичне рівняння за наступною формулою:
 (1.11)
(1.11)
де =a11+ a22;
=a11+ a22;
 =
a11*a22
- a11*a21.
=
a11*a22
- a11*a21.
Підставляючи коефіцієнти матриці Якобі отримуємо наступний вигляд
характеристичного рівняння:
 (1.12)
(1.12)
Відповідно корені характеристичного рівняння дорівнюють 0.
Так як у першому випадку det=0, то ми маємо пряму точок рівноваги, що аналогічно
другому випадку. Отже, аналогічні висновки по кореням характеристичного
рівняння можна застосувати і для другого випадку особливої точки.
1.4
Умови стійкості
Знайдемо слід та детермінант матриці Якобі за такими
формулами:
 (1.13)
(1.13)
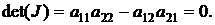 (1.14)
(1.14)
Так як детермінант і слід матриці системи дорівнюють 0, корені
характеристичного рівняння дорівнюють 0, з цього випливає, що всі положення
рівноваги нестійкі.
1.5
Фазовий портрет особливої точки
Побудуємо рівняння фазових траєкторій:
 (1.15)
(1.15)
 (1.17)
(1.17)
Де С - будь-яка константа.
Отже, фазові траєкторії лежать на прямих  і
паралельні прямій точок спокою.
і
паралельні прямій точок спокою.
Схематично зобразимо фазовий портрет системи:

Рисунок 1.1 - Фазовий портрет лінеаризованої системи
2. ЧИСЕЛЬНЕ МОДЕЛЮВАННЯ
ПОВЕДІНКИ СИСТЕМИ ПРИ РІЗНИХ ЗНАЧЕННЯХ ПАРАМЕТРІВ
2.1
Випадок лінеаризованої системи
Розглянемо випадки, коли параметри a, r системи 1.8 приймають різні значення.
Перший випадок: a>0, r>0.
Задамо значення параметрів a, r системи 1.8. Отримаємо:
 (2.1)
(2.1)
При даних значеннях отримаємо систему наступного вигляду:
 (2.2)
(2.2)
Знаходимо матрицю Якобі отриманої системи, як частинні
похідні по u та v:
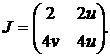 (2.3)
(2.3)
Знайдемо детермінант та слід матриці відповідно до формул 1.13 та 1.14:
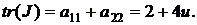 (2.4)
(2.4)
 (2.5)
(2.5)
Підставляючи координати особливої точки (0;0) отримаємо випадок, коли
детермінант і слід матриці дорівнюють 0. За даних умов отримаємо наступний вид
характеристичного рівняння:
|
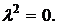 (2.6) (2.6)
|
|
Корені характеристичного рівняння дорівнюють 0. Отже система
має пряму точок рівноваги.
Фазові траєкторії лежать на прямій, що має вигляд:
|
 (2.7) (2.7)
|
|
Отже отримаємо наступний фазовий портрет:

Рисунок 2.1 - Фазовий портрет лінеаризованої системи
Використовуючи засоби MathCad побудуємо векторне поле даної
системи (Рисунок 2.3) за наступним алгоритмом:

Рисунок 2.2 - Алгоритм побудови векторного поля
лінеаризованої системи

Рисунок 2.3 - Векторне поле лінеаризованої системи
Другий випадок: a<0, r>0,
Задамо значення параметрів a, r системи 1.8. Отримаємо:
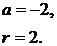 (2.8)
(2.8)
При даних значеннях отримаємо систему наступного вигляду:
 (2.9)
(2.9)
Аналогічно до попередніх результатів знаходимо матрицю Якобі, її
детермінант та слід:
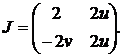 (2.10)
(2.10)
 (2.11)
(2.11)
 (2.12)
(2.12)
Підставляючи координати особливої точки (0;0) отримаємо випадок, коли
детермінант і слід матриці дорівнюють 0, а також корені характеристичного рівняння
дорівнюють 0. Отже система також має пряму точок рівноваги.
Фазові траєкторії лежать на прямій, що має вигляд:
 (2.13)
(2.13)
Отже отримаємо наступний фазовий портрет:

Рисунок 2.4 - Фазовий портрет лінеаризованої системи
Використовуючи засоби MathCad побудуємо векторне поле даної системи
(Рисунок 2.6) за наступним алгоритмом:

Рисунок 2.5 - Алгоритм побудови векторного поля лінеаризованої системи
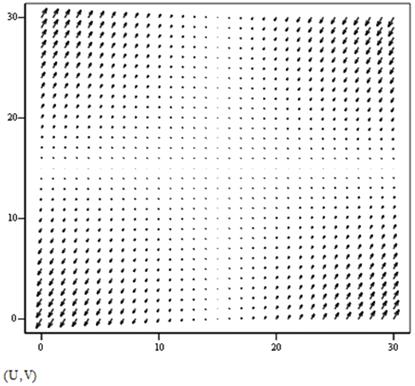
Рисунок 2.6 - Векторне поле лінеаризованої системи
Третій випадок: a>0, r<0.
Задамо значення параметрів a, r системи 1.8. Отримаємо:
 (2.14)
(2.14)
При даних значеннях отримаємо систему наступного вигляду:
 (2.15)
(2.15)
Аналогічно до попередніх результатів знаходимо матрицю Якобі, її
детермінант та слід:
особливий модель лінеаризований фазовий
 (2.16)
(2.16)
 (2.17)
(2.17)
 (2.18)
(2.18)
Підставляючи координати особливої точки (0;0) отримаємо випадок, коли
детермінант і слід матриці дорівнюють 0, а також корені характеристичного
рівняння дорівнюють 0. Отже система також має пряму точок рівноваги.
Фазові траєкторії лежать на прямій, що має вигляд:
 (2.19)
(2.19)
Отже отримаємо наступний фазовий портрет:

Рисунок 2.7 - Фазовий портрет лінеаризованої системи
Використовуючи засоби MathCad побудуємо векторне поле даної системи
(Рисунок 2.9) за наступним алгоритмом:
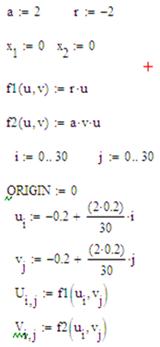
Рисунок 2.8 - Алгоритм побудови векторного поля лінеаризованої системи

Четвертий випадок: a<0, r<0.
Задамо значення параметрів a, r системи 1.8. Отримаємо:
 (2.20)
(2.20)
При даних значеннях отримаємо систему наступного вигляду:
 (2.21)
(2.21)
Аналогічно до попередніх результатів знаходимо матрицю Якобі, її
детермінант та слід:
 (2.22)
(2.22)
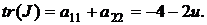 (2.23)
(2.23)
 (2.24)
(2.24)
Підставляючи координати особливої точки (0;0) отримаємо випадок, коли
детермінант і слід матриці дорівнюють 0, а також корені характеристичного
рівняння дорівнюють 0. Отже система також має пряму точок рівноваги.
Фазові траєкторії лежать на прямій, що має вигляд:
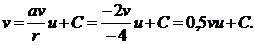 (2.25)
(2.25)
Отже отримаємо наступний фазовий портрет:
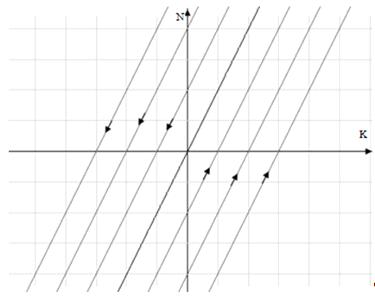
Рисунок 2.10 - Фазовий портрет лінеаризованої системи
Використовуючи засоби MathCad побудуємо векторне поле даної системи
(Рисунок 2.12) за наступним алгоритмом:

Рисунок 2.11 - Алгоритм побудови векторного поля лінеаризованої системи

Рисунок 2.12 - Векторне поле лінеаризованої системи
2.2
Випадок нелінійної системи
Для порівняння нелінійної системи із лінеаризованою задамо
аналогічні значення параметрів в системі та побудуємо векторне поле та фазовий
портрет.
Отримаємо систему наступного вигляду для першого випадку
параметрів (2.1):
 (2.26)
(2.26)
Знаходимо матрицю Якобі отриманої системи, як частинні похідні по K
та N:
 (2.27)
(2.27)
Підставляючи координати особливої точки (0;0) отримаємо випадок, коли
детермінант і слід матриці дорівнюють 0. За даних умов отримаємо наступний вид
характеристичного рівняння:
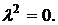 (2.28)
(2.28)
Корені характеристичного рівняння дорівнюють 0. Отже система має пряму
точок рівноваги.
Побудуємо рівняння фазових траєкторій:
 (2.29)
(2.29)
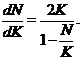 (2.30)
(2.30)
Фазові траєкторії лежать на прямій, що має наступний вигляд:
 (2.31)
(2.31)
Маємо наступний фазовий портрет:

Рисунок 2.13 - Фазовий портрет нелінійної системи
Використовуючи засоби MathCad побудуємо векторне поле даної системи
(Рисунок 2.15) за наступним алгоритмом:

Рисунок 2.14 - Алгоритм побудови векторного поля нелінійної системи

Рисунок 2.15 - Векторне поле лінеаризованої системи
Відповідно до випадку (2.8):
 (2.32)
(2.32)
Знаходимо матрицю Якобі отриманої системи:
 (2.33)
(2.33)
Підставляючи координати особливої точки (0;0) отримаємо випадок, коли
детермінант і слід матриці дорівнюють 0. Корені характеристичного рівняння
дорівнюють 0.
Побудуємо рівняння фазових траєкторій:
 (2.34)
(2.34)
 (2.35)
(2.35)
Фазові траєкторії лежать на прямій, що має наступний вигляд:
 (2.36)
(2.36)
Маємо наступний фазовий портрет:

Рисунок 2.16 - Фазовий портрет нелінійної системи
Використовуючи засоби MathCad побудуємо векторне поле даної системи (Рисунок 2.18) за наступним
алгоритмом:

Рисунок 2.17 - Алгоритм побудови векторного поля нелінійної системи
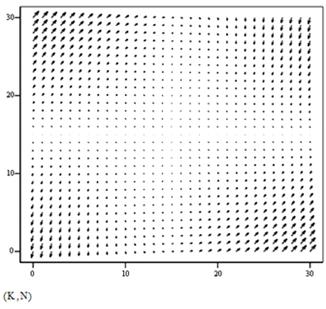
Рисунок 2.18 - Векторне поле лінеаризованої системи
Відповідно для випадку (2.14):
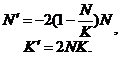 (2.37)
(2.37)
Знаходимо матрицю Якобі отриманої системи:
 (2.38)
(2.38)
Підставляючи координати особливої точки (0;0) отримаємо випадок, коли
детермінант і слід матриці дорівнюють 0. Корені характеристичного рівняння
дорівнюють 0.
Побудуємо рівняння фазових траєкторій:
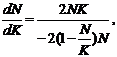 (2.39)
(2.39)
 (2.40)
(2.40)
Фазові траєкторії лежать на прямій, що має наступний вигляд:
 (2.41)
(2.41)
Маємо наступний фазовий портрет:
Рисунок 2.19 - Фазовий портрет нелінійної системи
Використовуючи засоби MathCad побудуємо векторне поле даної системи (Рисунок 2.21) за наступним
алгоритмом:

Рисунок 2.20 - Алгоритм побудови векторного поля нелінійної системи
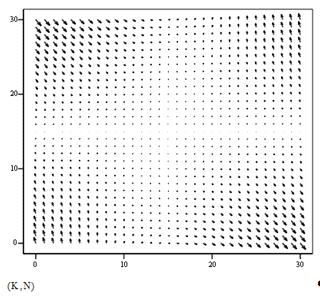
Рисунок 2.21 - Векторне поле лінеаризованої системи
Відповідно для випадку (2.20):
 (2.42)
(2.42)
Знаходимо матрицю Якобі отриманої системи:
 (2.43)
(2.43)
Підставляючи координати особливої точки (0;0) отримаємо випадок, коли
детермінант і слід матриці дорівнюють 0. Корені характеристичного рівняння
дорівнюють 0.
Побудуємо рівняння фазових траєкторій:
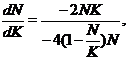 (2.44)
(2.44)
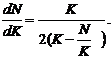 (2.45)
(2.45)
Фазові траєкторії лежать на прямій, що має наступний вигляд:
 (2.46)
(2.46)
Маємо наступний фазовий портрет:

Рисунок 2.22 - Фазовий портрет нелінійної системи
Використовуючи засоби MathCad побудуємо векторне поле даної системи (Рисунок 2.24) за наступним
алгоритмом:
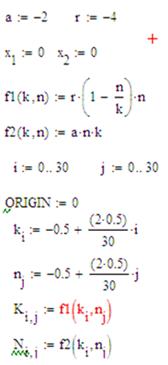
Рисунок 2.23 - Алгоритм побудови векторного поля нелінійної системи

Рисунок 2.24 - Векторне поле лінеаризованої системи
Так як у відповідності до теореми Хартмана-Гробмана, якщо коефіцієнти
матриці Якобі лінеаризованої системи мають нульові коефіцієнти, не можна нічого
сказати про нелінійну систему. Для можливості перенесення результатів
дослідження лінеаризованої системи на нелінійну було проведено дослідження обох
систем при різних варіантах вхідних параметрів і виявилось, що поведінка систем
співпадає при відповідній рівності параметрів.
Отже, ми можемо перенеси висновки досліджень із лінеаризованої системи
на нелінійну.
2.3
Економічна інтерпретація отриманих результатів дослідження
Розглянута моделі росту популяцій Ферхюльста складається із
системи двох диференційних рівнянь, які залежать від двох параметрів.
Змінні K i N повинні бути додатні, так як це
рівень технологічного розвитку та населення Землі відповідно. У першому випадку
розглядався випадок особливої точки, коли дані змінні дорівнюють 0, що не має
ніякого економічного змісту і настання такої ситуації неможливе у реальному
економічному середовищі. Досліджувана система виявилася нестійкою.
В результаті дослідження першого випадку особливої точки було
зроблено висновок, що вона є однією з точок рівноваги, що лежать на прямій.
Отже економічний зміст другого випадку положення рівноваги для моделі
аналогічний до вже розглянутого. Не існує ситуацій, коли населення Землі чи
рівень технологічного розвитку нульові.
ВИСНОВОК
У результаті виконання даної курсової роботи було розглянуто моделі росту популяцій Ферхюльста.
У відповідності до поставлених завдань:
Було знайдено особливі точки системи. Дана система має два
випадки особливих точок рівноваги, при дослідженні яких виявили, що точка
рівноваги (0;0) лежить на прямій особливих точок і є її початком. Досліджено систему на стійкість. Дана
система є нестійкою.
У відповідності до теореми Хартмана-Гробмана не можна було
нічого сказати про нелінійну систему, так як у матриці Якобі присутні нульові
значення. Для можливості перенесення результатів лінеаризованої системи на
нелінійну було проведено дослідження поведінки системи при різних значеннях
параметрів. Побудовані фазові портрети та векторні поля лінеаризованої системи
порівнювались із нелінійною системою і виявилось, що результати дослідженої
лінеаризованої системи можна перенести на нелінійну систему.
З точки зору реальної економіки особлива точка з координатами
(0;0) не має економічного змісту. При даних умовах населення Землі та рівень
технологічного розвитку дорівнюють 0, що неможливо у реальному економічному
середовищі.
СПИСОК
ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Кочура, Є.В. Моделювання макроекономічної динаміки
[Текст] : навч. посіб. / Є.В. Кочура, В.М. Косарів. - Київ: Центр навчальної
літератури, 2003. - 236 с. - ISBN 5-279-03037-6.
2. Беллман, P. Дифференциально-разностные уравнения
[Текст] / Р. Беллман, К. Кук. - М : МИР, 1967. - 548 с. - ISBN 5-256-0081-7.
. Кирьянов, Д.В. Самоучитель Mathcad 12 [Текст] / Д.В.
Кирьянов. - СПб.: БХВ-Петербург, 2005. - 576 c. - ISBN 5-94157-522-Х.
. Клебанова, Т.С. Моделирование экономической динамики
[Текст] : учеб. пособие / Т.С. Клебанова, Н.А. Дубровина, О.Ю. Полякова [и
др.]. - Х.: ИД «ИНЖЭК», 2005. - 244 с. - ISBN 966-8515-99-4.
. Милованов, В.П. Неравновесные
социально-экономические системы: синергетика и самоорганизация : [Текст] / В.П.
Милованов. - М.: Эдиториал УРСС, 2001. - 264 с. - ISBN 5-8360-0301-7.
. Пугачева, Е.Г. Самоорганизация социально-экономических
систем [Текст] : учеб. пособие / Е.Г. Пугачева, К.Н. Соловьенко. - Иркутск:
Изд-во БГУЭП, 2003. - 172 с. - ISBN 5-7253-0834-0.