Высшая математика

Высшая математика

1.      Решить систему линейных уравнений методом Крамера, методом обратной матрицы, методом Гаусса

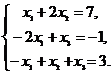
а) Метод Крамера

Обозначим через∆ = │А│, │А│- это определитель третьего порядка, т.к. три строчки и три столбца.

Формула для определителя третьего порядка имеет вид:

∙

При вычислении определителя третьего порядка удобно пользоваться правилом треугольников, которое символически можно записать следующим образом:

∆= │А│=1

Обозначим через ∆₁ определитель матрицы А, полученный заменой первого его столбца столбцом свободных членов.

Через ∆₂ определитель матрицы А, полученный заменой второго его столбца столбцом свободных членов.

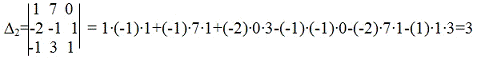
Через ∆₃ определитель матрицы А, полученный заменой третьго его столбца столбцом свободных членов.

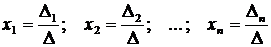
Найдем: х₁=1∕1 =1

х₂=3∕1=3

х₃=1∕1=1

ОТВЕТ: (1;3;1)

б) Метод обратной матрицы

Понятие обратной матрицы вводится только для квадратных матриц.

Квадратной матрицей называется та матрица у которой число строк равно числу столбцов.

Матрица А квадратная.

Находим обратную матрицу к матрице А. А≠0

Вычислить обратную матрицу можно по формуле:

,

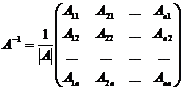Дана матрица

Найти матрицу, обратную данной. Проверить, что AA^-1 = E.

Вычислим определитель матрицы разложением по первой строке

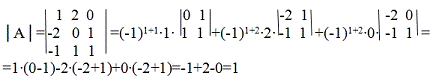
Найдем все алгебраические дополнения

Минором M_ij элемента a_ij определителя n-го порядка (n > 1) называется определитель (n - 1)-го порядка, полученный из определителя n-го порядка вычеркиванием i-й строки и j-го столбца, на пересечении которых стоит данный элемент a_ij.

Алгебраическим дополнением элемента a_ij называется число A_ij = (-1)^i+j M_ij.

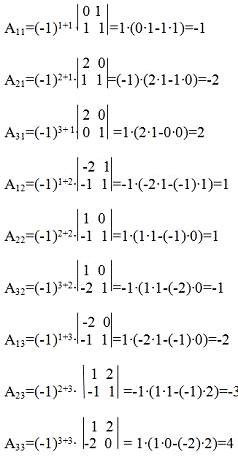
Находим х по формуле

х=А^-1∙В, где В это свободные члены уравнения

Сделаем проверку

матрица производная вектор уравнение

Ответ:  ; (1;3;1)

в) Метод Гаусса

Суть метода заключается в том, что с помощью элементарных преобразований СЛУ приводят к эквивалентной ступенчатой системе:

Элементарные преобразования СЛУ

1.   Перестановка любых двух уравнений.

2.      Почленное умножение любого уравнения системы на произвольное ненулевое число.

.        Почленное прибавление к некоторому уравнению системы любого другого ее уравнения, умноженного на произвольное число.

.        Вычеркивание в системе нулевого уравнения, т. е. уравнения вида:

× x₁ + 0 × x₂ + … +0 × x_n = 0.

Запишем расширенную матрицу ситемы и будем к ней применять элементарные преобразования, добиваясь ступенчатого вида.

)Из второй строки вычитаем третью

)Складываем первую строку с полученной второй

Система уравнений приняла вид

Подставляем найденные значения в третье уравнение

+3+х₃=3

х₃=3+1-3

х₃=1

2.      Даны векторы =(3,1,-1) и =(0,1,1). Найти их длины и скалярное произведение. Являются ли эти векторы ортогональными?

Найдем длины векторов по формуле

.

││= = =

││=  = =

Найдем скалярное произведение векторов по формуле

.

∙=3∙0+1∙1+(-1)∙1=0,

значит векторы  и  ортогональные

Ответ : ││=, ││=

3. Написать уравнение прямой, проходящей через точку А(2;3) параллельно направляющему вектору =(-1;-2). Найти расстояние от точки В(1;4) до полученной прямой

Вектор, параллельный данной прямой или лежащий на ней, называется направляющим вектором этой прямой.

Пусть прямая проходит через точку М₀ (x₀;y₀) и имеет направляющий вектор q̅=(λ;β)

Тогда ее уравнение имеет вид

y-y₀ = x-x₀

βλ

Подставляем в данное уравнение координаты точки А и вектора

Получим

(y-3)=-2(x-2)

y+3= -2x+4

x -y-1=0

Уравнение прямой 2x-y-1=0

Пусть задана прямая уравнением Ax + By + C=0 и точка M₀ (x₀;y₀). Расстояние d от точки M₀до прямой вычисляется по формулеЭ

В (1;4) уравнение прямой 2x-y-1=0

│2∙1-1∙4-1│ │-3│

d = √2²+(-1)² = √5 =0,6√5

Ответ: уравнение 2x-y-1=0 расстояние 0,6√5

4. Вычислить пределы: а) ; б) ; в) .

а) lim (1-4x)= lim 1- lim 4x=1- 4∙(-2)=9 →-2 x →-2 x →-2

), где c - любое число.

), где c - любое число.

).

б) Предел числителя и знаменателя дроби  при x ® 1 равен нулю (в таких случаях говорят, что имеем неопределенность вида ). Для раскрытия этой неопределенности разложим числитель и знаменатель на множители (в числителе применим формулу разложения квадратного трехчлена на множители, в знаменателе - формулу разности квадратов) и сократим дробь. Получим:

.

.

в)=при x ® ¥ стремятся к¥ (имеем дело с неопределенностью вида ). Для нахождения предела данной дроби разделим числитель и знаменатель дроби на старшую степень x, т. е. на x³, получим

lim3x³-5 = lim3- x³= 3 = - 1→∞ 7-2x-3x³ x→∞ 7 -2 -3-3

x³x²

так как при x ® ¥ каждая из дробей стремится к нулю.

Ответ:

а) =9

б) =2

в) =-1

5. Найти производные функций одной переменной и частные производные первого порядка функций двух переменных: а) ; б) ; в) ;        г) .

а);

Применяем формулы

1. C¢ = 0.

. (Cu)¢ = Cu¢.

3. (u ± v)¢ = u¢ ± v¢.

. (uv)¢ = u¢v + uv¢.

5. .

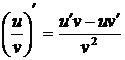б) ;

.

в)

При нахождении частной производной первого порядка функций двух переменных сначала дифференцируем как функцию одной переменной , другая предполагается постоянной.

Z´xзначит y-постоянная

Z´x=(5x³y²-xy)´=5y² ∙ 3x² -y∙1=15y²x²-y

Z´yзначитx - постоянная

Z´y=(5x³y²-xy)´=5x³∙2y-x∙1=10x³y-x

г)

Z´x=((x-2y)∙cosxy)´=(x-2y)´∙cosxy + (x-2y)∙(cosxy)´=1∙cosxy + (x-2y) ∙ (-sinxy) ∙∙(xy)´=cosxy + (x-2y) ∙ (-sinxy) ∙y = cosxy-xysinxy + 2y²sinxy

Z´y=((x-2y)∙cosxy)´= (x-2y)´∙cosxy + (x-2y)∙(cosxy)´=-2∙1∙cosxy + (x-2y) ∙ (-sinxy) ∙ ∙(xy)´=-2cosxy + (x-2y) ∙x∙(-sinxy)=-2 cosxy-x² sinxy + 2xysinxy

6. Найти неопределенный интеграл и проверить результат дифференцированием

а) ; б) ;

Интеграл от суммы (разности) двух функций равен сумме (разности) интегралов от этих функций

Изтаблица основных интегралов

. , a ≠ -1.

. , x ≠ 0.

.

а) =∫(x√x - 1∕x + 2)dx=∫x√xdx - ∫dx/x +2dx=

x^3/2+1x^2/5

∫x∙x^1/2dx-∫dx/x +∫2dx=∫x^3/2dx - ∫dx/x+∫2dx=3/2+1 -ln│x│+2x+c=5/2 -ln│x│

+2x+c=3/2+1=2.5

x^2.5x^2.5∙2

5/2 = 5

x^2.5∙2

-ln│x│ +2x +c=0,4x^2.5-ln│x│+2x +c

Проверка

(0,4х^2,5-ln│x│+2x+c)′=(0,4x^2.5)′-(ln│x│)′+(2x)′+c′=0,4∙2.5∙x^1.5-1/x+2=x^1.5-1/x+2=x√x-1/x+2

б)

Введем подстановку 2-5x=t, тогда dt=d(2-5x)=(2-5x)´dx=-5dx

dt = -5dx=dt/-5 dx=-1/5dt

=∫t⁷∙(-1/5)dt=-1/5∫t⁷dt=-1/5∙t⁸/8 +c=-1/40∙t⁸+c= заменяемt=2-5x, получаем

-1/40(2-5x)⁸+c

Проверка

(-1/40(2-5х)⁸+с)′=-1/40∙8∙(2-5х)⁷∙(2-5х)′+с′=-1/5(2-5х)⁷∙(-5х)=(2-5х)⁷

Ответ: а) 0,4x^2.5-ln│x│+2x +c

б)-1/40(2-5x)⁸+c

7. Найти определенный интеграл.

Найдем определенный интеграл по формуле Ньютона-Лейбница.

Если функция y = f(x) непрерывна на отрезке [a; b] и F(x) - некоторая ее первообразная, то

.

Если ввести обозначение , то формула Ньютона -Лейбница примет вид

.

∫=(2-3x⁴ +x)dx= ∫2dx - 3 ∫x⁴dx + ∫xdx=(2x-3∙x⁵/5+x²/2)│ =

=(2∙1-3∙1⁵/5+1²/2)-(2∙(-1)-3∙(-1)⁵/5+(-1)²/2)=(2-3/5+1/2)-(-2+3/5+1/2)=

=2-3/5+1/2+2-3/5-1/2=2,8

Ответ: =2,8

8. Исследовать на экстремум z= 4+3x-x²-2y-y²

Найдем частные производные первого порядка

z′_x= 3-2x; z′_y= -2-2y

Найдем критические точки, это точки в которых производная равна нулю, либо не существует. Имеем критическую точку М(1,5;-1)

Частные производные второго порядка

z″_xx=(3-2x)′=-2

z″_xy=(3-2x)′=0

z″_yy=-2

НаходимD=z″_xx∙z″_yy-(z″_xy)²=-2∙(-2)-0=4

Т.к. D>0 и z″_xx<0, то точка М(1,5;-1)является точкой максимума.

Находим экстремумы функции

z_max=z(1,5;-1)=4+3∙1,5-1,5²-2∙(-1)-(-1)²=7,25

Ответ:z_max=z(1,5;-1)=7,25

9. Студент сдает сессию из двух экзаменов. Он добросовестно подготовился и считает, что на каждом экзамене получит «4» с вероятностью , «два» получить не может, а получение «три» и «пять» для него равновероятно. Какова вероятность того, что а) он сдаст сессию без троек; б) сдаст сессию на «отлично»?

Введем обозначения Оценка 3 - А Р(А)=0,05

Оценка 4 - В Р(В)=0,9

Оценка 5 - С Р(С)=0,05

Воспользуемся теоремой сложения и умножения вероятностей

Р(А+В)=Р(А)+Р(В)-Р(АВ)

события А и В несовместимы

Р(А∙В)=Р(А)∙Р(В)

а)Р(В+С)=Р(В)+Р(С)-Р(В∙С)=0,9+0,05-0,9∙0,05=0,9+0,05-0,045=0,905

вероятность сдачи сессии без троек

в) Р(Ᾱ∙В̅)=(1-0,05)∙(1-0,9)=0,95∙0,1=0,095

вероятность сдачи сессии на отлично

ОТВЕТ: а) 0,905

в) 0,095

11. На первом курсе 70 студентов. Из них 30 человек занимаются физкультурой в секции гимнастики, 20 - в секции лыжного спорта, остальные - легкоатлеты. Вероятность получить зачет «автоматом» у гимнастов - 0,8; у лыжников - 0,85; у легкоатлетов - 0,75. Найти вероятность того, что наудачу выбранный с курса студент получит зачет по физкультуре автоматически

А - это событие

Р(А) - это вероятность события А

Введем гипотезы

H₁ - зачет автоматом получил гимнаст

H₂ - зачет автоматом получил лыжник

H₃ - зачет автоматом получил легкоатлет

Значит Р(A/ H₁) = 0,8

Р(А/ H₂) = 0,85

Р(А/ H₃) = 0,75

-(30+20)=20 легкоатлетов

Вероятность того, что автоматом зачет получит гимнаст будет

Р(H₁)==

Лыжник Р(H₂)==

легкоатлет Р(H₃)==

По формуле полной вероятности

Вычислим

Р(А)= ∙ 0,8 + ∙ 0,85 + ∙ 0,75= ∙ + ∙ +∙ =++=

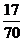==0,8

ОТВЕТ: 0,8

. В таблице дан закон распределения случайной величины (месячная выручка киоска «Роспечать»). Найти математическое ожидание и дисперсию этой случайной величины

Многоугольник распределения случайной величины X имеет вид:

а) Найдем математическое ожидание случайной величины X:

Математическое ожидание равно сумме произведений всех возможных значений X на соответствующие вероятности

М(х)=115∙+105∙+95∙+90∙+85∙+65∙=

=2,875+21+47,5+18+4,25+1,625= 95,25

б) Найдем дисперсию случайной величины X:

Дисперсией дискретной случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Для вычисления дисперсии удобно использовать формулу

D(x)=M(x²) - M²x

M(x²)= 115²∙+105²∙+95²∙+90²∙+85²∙+65²∙=

= 330,625+2205+4512,5+1620+361,25+105,625=9135

D(x)=9135-95.25²=9135-9072,5625=62,4375

Среднее квадратическое отклонение случайной величины

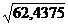==7,90174037,90

ОТВЕТ: М(х)= 95,25 D(x)= 62,4375 s(х) 7,90