Проектирование алгоритма вычисления элементарной функции с использованием таблично-алгоритмического метода

Проектирование алгоритма вычисления элементарной функции с использованием таблично-алгоритмического метода

Техническое задание

1.      Выполнить проектирование алгоритма вычисления элементарной функции с использованием таблично-алгоритмического метода в соответствии с заданным вариантом. Алгоритм предназначен для целочисленных вычислений в дополнительном коде в формате «байт со знаком».

.        Выполнить расчет параметров алгоритма.

.        Выполнить масштабирование алгоритма и получить целочисленный алгоритм вычисления заданной функции.

.        Разработать MatLab-программу для экспериментального анализа полной, вычислительной и методической погрешностей целочисленного алгоритма.

.        Используя разработанную программу, получить значения элементарной функции, а также методической, инструментальной и полной погрешностей целочисленного алгоритма для текущих значений аргумента из заданного интервала аппроксимации. Построить графики указанных величин на интервале аппроксимации.

.        Разработать блок-схему подпрограммы вычисления элементарной функции по разработанному алгоритму в целочисленном формате данных.

.        Разработать подпрограмму вычисления элементарной функции на языке Ассемблер IBM PC, реализующую разработанный алгоритм.

.        Сопоставить экспериментальные значения погрешностей с их теоретическими оценками и сделать выводы.

Содержание

Введение

.        Теоретические основы таблично-алгоритмического метода

.        Постановка задачи проектирования алгоритма вычисления функции

.        Расчет параметров алгоритма

.        Масштабирование алгоритма

.        Блок-схема модели для экспериментального анализа погрешностей алгоритма

.        Описание и листинг программы

.        Результаты моделирования

.        Подпрограмма вычисления функции на языке Ассемблер IBM PC

Заключение

Список использованных источников

Введение

Функции одного аргумента, значения которых получаются с помощью конечного числа вычислительных операций над аргументом, зависимой переменной и постоянными числами, называются элементарными.

Для того чтобы вычислить функцию на всем интервале аргумента, выполняются следующие действия:

- значения аргумента приводятся к интервалу аппроксимации;

- вычисляются значения элементарной функции для приведенного значения аргумента;

- выполняется постобработка полученного значения функции.

Существующие методы вычисления элементарных функций можно разделить на три вида:

- алгоритмический метод;

- табличный метод;

- таблично-алгоритмический метод.

В случае алгоритмического метода элементарная функция вычисляется, как правило, с помощью степенного многочлена. Данный метод требует минимального объема памяти, но занимает значительное время вычислений. В случае табличного метода значения функции вообще не вычисляются, поскольку для всех возможных значений аргумента в памяти компьютера хранятся готовые значения функции в виде таблицы. Это самый быстрый метод, но при увеличении разрядности аргумента объем таблицы становится чрезмерно большим. В основу таблично-алгоритмического метода также положена таблица значений функции, но она строится не для всех значений аргумента, а для ограниченного ряда табличных значений. Если текущее значение аргумента отличается от табличного, то из таблицы извлекается ближайшее грубое значение функции, а затем вычисляется поправка по одному из численных методов. Таблично-алгоритмический метод сочетает в себе достоинства первых двух методов и получил наибольшее распространение в микропроцессорах и микроконтроллерах. Вычисление значений элементарных функций - один из наиболее часто встречающихся типов математических операций, выполняемых в микроконтроллерах при решении задач управления движением роботов-манипуляторов, навигации, стабилизации, цифровой фильтрации и т.д. Общая доля этих операций может составлять 3-5%, а время, которое требуется для их программной реализации, - 50% времени решения всей задачи.

В этой связи приобретает важное значение разработка алгоритмов вычисления элементарных функций для их программной и аппаратной реализации в микропроцессорах и микроконтроллерах.

1. Теоретические основы таблично-алгоритмического метода

В основе таблично-алгоритмического метода лежит разбиение интервала аппроксимации функции f(x) на равные промежутки величиной h (рис.1):

Рис.1. Разбиение интервала аппроксимации

В результате разбиения образуются значения аргумента x_s, которые в дальнейшем называются табличными. Для каждого x_s вычисляется значение функции f(x_s), которое также называется табличным. Полученные значения x_s и f(x_s) сводятся в таблицу, которая размещается в памяти компьютера (рис.2). Если таблично-алгоритмический метод использует и производные вычисляемой функции, то аналогичным образом формируется таблица значений производных. Табличные значения функции и производных получают один раз на этапе разработки алгоритма.

Рис.2. Таблица значений аргумента и функции

В дальнейшем вычисление функции f(x) для произвольного значения x на интервале аппроксимации от x_min до x_max выполняется следующим образом. Сначала определяется интервал разбиения x_s£x£ x_s+h, в котором находится значение x. С этой целью вычисляется индекс таблицы i, который является адресом табличных значений x_s и f(x_s):

=[(x-x_min)/h]^-_ц , (1)

где [·]^-_ц - оператор округления до целого значения с недостатком. После этого искомое значение функции вычисляется по алгоритму

где φ(x_s,Ñx) - это поправка, которая уточняет табличное значение функции f(x_s); Ñx=x- x_s - разность между текущим и табличным значением аргумента, причем Ñx_max = h.

В частности, поправку φ(x_s,Ñx) можно вычислить, используя метод линейной интерполяции. Тогда алгоритм (2) принимает следующий вид:

(x)=f(x_s)+ (x - x_s)∙[ f(x_s+h) - f (x_s)]/h= f(x_s)+ Ñx ∙[ f(x_s+h) - f (x_s)]/h, (3)

где f(x_s+h) - соседнее табличное значение функции.

Вычисление функции по алгоритму (3) можно представить графически (рис.3):

вычислительный погрешность алгоритмический ассемблер

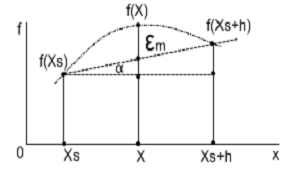
Рис.3. Вычисление значения функции

Из рис.3 видно, что поправка φ(x_s,Ñx) определяется как неизвестный катет прямоугольного треугольника по известному катету

Ñx=x-x_s и tg(a)=[ f(x_s+h) - f (x_s)]/h.

Алгоритм (3) обладает методической погрешностью

ε_м≤ Ñx(Ñx- h) ∙ |f ⁽²⁾|_max / 2 , (4)

где |f ⁽²⁾|_max - максимальный модуль второй производной на интервале аппроксимации.

Таким образом шаг h является главным параметром алгоритма, который определяет величину методической погрешности.

2. Постановка задачи проектирования алгоритма вычисления функции

Одной из задач проектирования алгоритмов таблично-алгоритмического метода является удовлетворение требований по времени и точности вычисления элементарной функции.

Требование по времени вычислений можно выполнить, ограничивая такие параметры численного метода вычисления поправки, как число членов ряда, полинома, цепной дроби или количество итераций и т.п. При этом учитывается время выполнения в микроконтроллере арифметических, логических и прочих операций, необходимых для реализации алгоритма. В курсовой работе обеспечивается минимальное время вычислений путем задания одного из простейших методов вычисления поправки.

Требуемая точность вычислений может задаваться в виде относительной погрешности или опосредованно через разрядность представления данных в микроконтроллере, как в данной курсовой работе. Ниже приводится методика удовлетворения требования по точности вычислений для последнего случая.

Проектируемый алгоритм обладает полной погрешностью, значение которой можно представить в виде суммы

ε=ε_м+ε_в,

где ε_м - методическая погрешность; ε_в - вычислительная (инструментальная) погрешность, которая зависит от разрядности данных, количества, типа и последовательности операций, составляющих алгоритм (а также от выбранных масштабов в случае вычислений в целочисленном формате данных). Для удовлетворения требования по точности вычислений устанавливается следующее соотношение между методической и вычислительной погрешностями в виде баланса:

ε_м≤ ε_в . (5)

Погрешность ε_в можно оценить аналитически. Однако такая оценка получается громоздкой и слишком грубой. Задачу можно упростить, если вместо исходного баланса (5) потребовать более жесткий баланс погрешностей:

ε_м≤ε₀ , (6)

где ε₀ - погрешность представления переменных в целочисленном формате данных, причем

ε₀ ≤ 1/2М_f = |f|_max / 2(2^n-1-1), (7)

где М_f - масштаб функции f(x); n - разрядность. Заметим, что оценка ε_в≈ε₀ близка к реальной, поскольку количество арифметических операций в алгоритме (3) исчисляется единицами.

Для большинства элементарных функций на интервале аппроксимации выполняется равенство |f|_max ≤1, тогда получаем:

ε₀ ≤ 2^-n. (8)

Подставив в (6) оценку (4) для ε_м и оценку (8) для ε₀, получаем баланс погрешностей в виде

½Ñx(Ñx- h) ∙ |f ⁽²⁾|_max½ / 2 ≤ 2^-n. (9)

Левая часть данного соотношения достигает максимального значения при Ñx =h/2. Поэтому в окончательном виде баланс погрешностей принимает вид

² ∙ |f ⁽²⁾| _max / 8 ≤ 2^-n. (10)

Баланс (10) позволяет найти шаг таблицы h, исходя из заданной разрядности формата данных n.

3. Расчет параметров алгоритма

Для нахождения шага таблицы представим его в виде h=2^-s. Тогда из баланса (10) получаем

≥ [n + log₂|f ⁽²⁾| _max- 3]/2. (11)

Параметр s, найденный из (11), округляется до целого значения с избытком.

Данный параметр обеспечивает баланс методической и вычислительной погрешностей алгоритма. Кроме того, он определяет не только шаг таблицы h=2^-s, но и количество табличных значений функции f(x), равное 2^s.

Так как разрядность n известна, то для нахождения параметра s по формуле (10) необходимо определить максимальный модуль второй производной |f ⁽²⁾| _max на интервале аппроксимации. Для этого достаточно построить график второй производной (например, с помощью программы MatLab (рис.4).

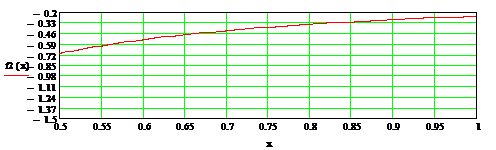
Рис.4. Графики второй производной

Из полученного графика второй производной находим |f⁽²⁾|_max= 0.707. Тогда, учитывая, что n=8, из (11) находим s ≥2,75. При округлении с избытком s=3. Тогда можно рассчитать шаг таблицы h=2^-s=2^-3=0.125.

x = sym(‘x’);(sin(x), x, 2)(‘-sin(x)’, [0.5 1])

4. Масштабирование алгоритма

Для выполнения вычислений в целочисленном формате данных любую вещественную величину (целые числа, правильные и неправильные дроби) необходимо представить в виде целого числа, которое можно разместить в заданном n-разрядном формате. Последнее можно достигнуть, выполнив масштабирование алгоритма. Найдем масштабы для величин x, f(x), f(x_s), f(x_s+h), x_s,Ñx и h, входящих в алгоритм (3). При этом будем исходить из форматов целочисленных аналогов этих величин X, F(X), F(X_s), F(X_s+H), X_s, ÑX и H, приведенных на рис.5.

Величины f(x), f(x_s) и f(x_s+h), имеют общий масштаб

_f ≤ (2^п-1-1)/|f|_max , (12)

где |f|_max определяется из графика функции на интервале аппроксимации.

Величины x, x_s,Ñx и h также имеют общий масштаб

М_x ≤ (2^n-1 -1)/ x_max . (13)

Масштабирование алгоритма (3) сводится к замене исходных вещественных величин эквивалентными отношениями соответствующих целочисленных значений к масштабам и приведению подобных. Учитывая, что H =2^(n-s-1), алгоритм (3) после масштабирования можно представить в виде

F(X) = F(X _s) +2^(n-s-1)∙ÑX ∙(F(X _s+H) - F(X _s)). (14)

Тогда из (14) вытекает следующий целочисленный алгоритм:

F(X) = F(X _s) +[2^-4(ÑX ∙(F(X _s+H) - F(X _s))]_ц^1/2, (15)

где [·]_ц^1/2 - оператор округления до целого значения по 1/2.

На рис.5 приведены форматы целочисленных величин, входящих в алгоритм (15).

Рис.5. Форматы целочисленных величин

5. Блок-схема модели для экспериментального анализа погрешностей алгоритма

Приведенная ниже модель обеспечивает нахождение полной ε, методической ε_м и вычислительной (инструментальной) ε_в погрешностей целочисленного алгоритма вычисления функции для текущих значений аргумента x из интервала аппроксимации.

7. Описание и листинг программы

В данном разделе приводится MatLab-программа, реализующая рассмотренную выше модель для экспериментального анализа полной ε, методической ε_м и вычислительной (инструментальной) ε_в погрешностей целочисленного алгоритма вычисления функции.

Листинг программы выглядит следующим образом:

clear

%Вычисление табличных значений аргумента и функции с шагом h=2^-3; %шаг таблицы= 0.5:h:1; %таблица значений аргумента= sqrt(xs); %таблица значений функции= 2^7;= 2^7;= round(xs*Mx); %таблица целочисленных значений аргумента= round(fs*Mf); %таблица целочисленных значений функции

%Вычисление текущих значений функции с шагом h/4= 0.5:h/4:1;=sqrt(x);(5,1,1); plot(x,fx,'g') %график функцииon;'Graphic sqrt(x)';=round(x*Mx);= floor((x-0.5)/h) +1; %значение индекса

%Вычисление не масштабированных значений функции

%по методу линейной интерполяцииj=1:1:17(i(j)<5)(j) = fs(i(j))+(x(j)-xs(i(j)))*((fs(i(j)+1)-fs(i(j)))/h);(j) = fs(i(j));;

%Вычисление значений функции по целочисленному алгоритму(i(j)<5)(j) = FS(i(j))+ round(2^-4*(X(j)-XS(i(j)))*(FS(i(j)+1)-FS(i(j))));(j) = FS(i(j));;

%Демаcштабирование значений функции= F/Mf;(5,1,2); plot(x,fdem,'g');on;'Graph f demash';

%Полная погрешность= sqrt(x) - fdem;(5,1,3); plot(x,eps,'b');on;'Graph polnoi pogreshnosti';

%Методическая погрешность_m = sqrt(x)- f;(5,1,4); plot(x,e_m,'r');on;'Graphic methodich pogreshnosti';

%Инструментальная погрешность_instr = f-F/Mf;(5,1,5); plot(x,e_instr,'-k');on;'Graphic instrum pogreshnosti';

. Результаты моделирования

Ниже изображены графики соответственно функции, полной ε, методической ε_м и вычислительной (инструментальной) ε_в погрешностей, полученные в результате выполнения MatLab-программы.

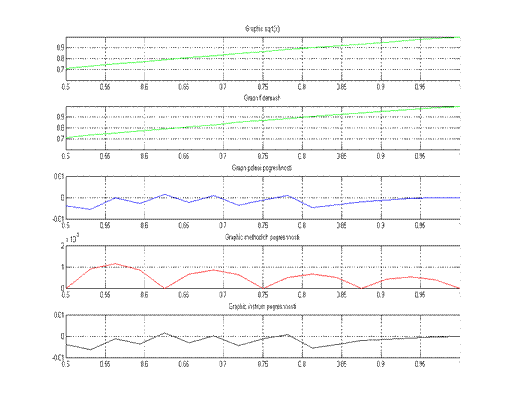
Заключение

1. В данной работе было выполнено проектирование алгоритма вычисления элементарной функции с использованием таблично-алгоритмического метода в соответствии с заданным вариантом.

. Разработана MatLab-программа для экспериментального анализа полной, вычислительной и методической погрешностей алгоритма.

. Получены экспериментальные значения элементарной функции, полной, вычислительной (инструментальной) и методической погрешностей.

. Анализируя полученные значения погрешностей можно сделать вывод о том, что разработанный алгоритм удовлетворяет требованиям технического задания, баланс погрешностей выполняется.

Список использованных источников

1.      Попов Б.А., Теслер Г.С. Вычисление функций на ЭВМ. Справочник - Киев: Наукова думка, 1984. - 599 с.

.        Ледовской М.И., Пьявченко О.Н. Методическое руководство к курсовой работе «Проектирование алгоритмов математических операций для микроЭВМ» по курсу «Основы обработки данных и моделирования» - Таганрог: Изд-во ТРТУ, 1999. - 30 с.

.        Ледовской М.И. Методическое руководство к выполнению лабораторных работ на модульной основе с диагностико-квалиметрическим обеспечением по дисциплине «Алгоритмические основы математических операций» - Таганрог: Изд-во ТТИ ЮФУ 2009. - 20 с.

.        Конспект лекций по курсу «Алгоритмические основы математических операций ч.2».