Исследование устойчивости алгоритмов приема к изменению помехи

ДИПЛОМНАЯ РАБОТА

Тема: Исследование устойчивости алгоритмов приема к изменению помехи

Реферат

 

Отчет, ____ с., 1 ч., 41 рис., 12 табл.,20 ист., 1 прил.

АСИМПТОТИЧЕСКИ ОПТИМАЛЬНЫЕ АЛГОРИТМЫ, РАНГОВЫЕ АЛГОРИТМЫ, ПОСЛЕДЕТЕКТОРНАЯ ОБРАБОТКА, ВЫДЕЛЕНИЕ ОГИБАЮЩЕЙ, НЕКОГЕРЕНТНЫЙ ПРИЕМ, ОБНАРУЖЕНИЕ УЗКОПОЛОСНОГО СИГНАЛА, КОЭФФИЦИЕНТ ОТНОСИТЕЛЬНОЙ АСИМПТОТИЧЕСКОЙ ЭФФЕКТИВНОСТИ, ВЕРОЯТНОСТЬ ОБНАРУЖЕНИЯ, КРИТЕРИЙ ХИ-КВАДРАТ, ДАТЧИК СЛУЧАНЫЙ ВЕЛИЧИН, ЛИНЕЙНЫЙ, ЗНАКОВЫЙ, МЕДИАННЫЙ, ВАН-ДЕР-ВАРДЕН АЛГОРИТМ

Объектом исследования являются асимптотически оптимальные и ранговые алгоритмы обнаружения сигнала - знаковый, линейный, медианный и алгоритм Ван-дер-Вардена.

Цель работы - оценка помехоустойчивости асимптотически оптимальных и ранговых обнаружителей сигнала по коэффициенту относительной асимптотической эффективности в условиях до и последетекторной обработки при некогерентном приеме. Реализация проверки случайных величин методом Хи-квадрат.

Оценка устойчивости производится с помощью метода статистического имитационного моделирования по коэффициенту относительной асимптотической эффективности. Результатом работы являются семейства вероятностных характеристик и зависимостей коэффициента относительной асимптотической эффективности от отношения С/Ш и распределения помех на входе.

В ходе исследования было показано, что эффективность АО алгоритмов снижается в условиях работы при чужой помехе, что подтверждается расчетом КАОЭ. По итогам имитационного моделирования последетекторных обнаружителей, работающих по вышеописанным алгоритмам, наблюдается выигрыш додетекторного приема над последетекторным. Результатом моделирования датчика случайных величин служит тестовый алгоритм, на основе критерия Хи - квадрат.

Содержание

 

Обозначения и сокращения

1. Введение

1.1 Анализ литературы

2. Алгоритмы обнаружения сигналов

2.1 Асимптотически оптимальные алгоритмы обнаружения сигналов

2.2 Ранговые алгоритмы обнаружения сигналов на фоне независимых помех

2.3 Асимптотически оптимальный алгоритм некогерентного приема узкополосного сигнала со случайной фазой

2.4 Последетекторный асимптотически оптимальный алгоритм обнаружения модулированного сигнала со случайной фазой (амплитудный метод)

3 Выделение огибающей узкополосного случайного процесса. Квадратурный демодулятор

4. Моделирование алгоритмов

4.1 АО и ранговые алгоритмы

4.2 Моделирование фильтра низкой частоты

4.3 Алгоритм моделирования обнаружителя узкополосного сигнала

4.4 Алгоритм моделирования последетекторного обнаружителя

4.5 Моделирование помехи

4.6 Отношение сигнал/шум

5. Рабочие характеристики алгоритмов

5.1 Додетекторное обнаружение

5.2 Последетекторное обнаружение

6. Коэффициент относительной асимптотической эффективности

7. Доверительные интервалы

8. Датчик случайных величин. Тестирование по критерию Хи-квадрат

9. Заключение

10. Список литературы

Приложения

Обозначения и сокращения

С - сигнал

С/Ш - отношение сигнал/шум

РТС - радиотехническая система

КАОЭ - коэффициент асимптотической относительной эффективности

ПУ - пороговое устройство

РУ - решающее устройство

К - коррелятор

ПО - правильное обнаружение

ЛТ - ложная тревога

ПС - пропуск сигнала

КВ - квадратор

АО - асимптотически оптимальный

СКО - среднеквадратическое отклонение

НП - Нейман-Пирсон

ФНЧ - фильтр нижних частот

НЧ - низкочастотная составляющая

ВЧ - высокочастотная составляющая

1. Введение

При реализации процедур обнаружения или различения сигналов результатом обработки должно быть принятие соответствующего решения. Так, в случае обнаружения необходимо принять решение относительно того, присутствует ли в сигнале , поступающем на вход устройства обработки, полезный сигнал  или же  представляет собой только помеху. При этом входной сигнал при наличии полезного сигнала представляется в виде:

 

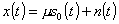, (1)

где  - аддитивная помеха;  - коэффициент, характеризующий затухание сигнала в процессе распространения.

Любые методы принятия решения или стратегии принятия решения сводятся в конечном счете к тому, что множество всех возможных реализаций входного случайного процесса  (реализацией которого является сигнал ) на интервале анализа  разбивается на  непересекающихся подмножеств, каждому из которых ставится во взаимно однозначное соответствие то или иное решение. В зависимости от того, какому из указанных подмножеств принадлежит анализируемый отрезок реализации , выносится соответствующее решение о том, что принятым является некоторый сигнал  из множества возможных . В частном случае обнаружения сигнала  имеются лишь два таких подмножества, так что принимается одно из двух возможных решений: "сигнал  присутствует" или "сигнал  отсутствует".

Таким образом, задача принятия решения сводится к задаче проверки статистической гипотезы о принадлежности анализируемой реализации  тому или иному подмножеству [1].

Центральным для всей проблемы выбора статистических решений является определение структуры решающего устройства, сводящееся к синтезу алгоритмов принятия решений при проведении радиотехнических экспериментов [2].

Таким образом, различные алгоритмы в большей или меньшей степени оптимальны в тех или иных помеховых условиях. В данной работе ставится задача моделирования и исследования устойчивости асимптотически оптимальных и ранговых алгоритмов при некогерентном приеме к изменению распределения помехи вида

. (2)

В этой связи были исследованы алгоритмы, АО при гауссовой помехе и помехе с распределением Лапласа (линейный и знаковый соответственно), а также ранговые алгоритмы, АО на фоне тех же помех (алгоритм Ван-дер-Вардена и медианный) [3].

Работа данных алгоритмов моделировалась как в условиях отсутствия детектирования огибающей случайного процесса, так и в условиях последетекторной обработки.

1.1 Анализ литературы

Актуальность рассматриваемой темы подтверждается во множестве публикаций, ниже приведены некоторые из них.

Так, например, в работе [8] рассмотрена адаптация непараметрических критериев в условиях зависимых исходных данных. Предложен подход к решению задачи адаптации, заключающийся в использовании специальных показателей зависимости наблюдений, устойчивых к изменению вида распределения исходных данных, к оценке этих показателей и к нахождению распределения рангов с учетом полученных оценок.

В ином источнике получены выражения для математического ожидания, дисперсии и условных вероятностей превышений исследуемыми отсчетами сигналов помехо-шумовых отсчетов знакового и рангового обнаружителей Неймана-Пирсона, которые позволяют осуществить расчеты характеристик обнаружителя в условиях совместного воздействия шума и потока помех с произвольными законами распределения [9].

Также предложены алгоритмы стабилизации вероятности ложной тревоги с использованием аппарата порядковых статистик в статье [10], вычисление медианы и среднего значения шума, имеющие малые вычислительные затраты и эффективно работающие в сложных помеховых условиях.

В работе [11] синтезированы оптимальные знаковый и ранговый обнаружители Неймана-Пирсона в условиях совместного воздействия шума и размытого (интенсивного) потока помех, в результате чего получены точные выражения отношений правдоподобия.

Изучена статья, в которой получены выражения для вероятностей ложной тревоги и правильного обнаружения при использовании 2х порогового обнаружителя радиосигнала при наличии имитирующих помех и гауссовского шума [12]. Показано, что селективные свойства обнаружителя по отношению к имитирующим помехам снижаются при значениях коэффициента корреляции сигнала и помехи более 0,6, и практически утрачиваются при значениях более 0,9.

В публикации [13] проведён обзор основных решающих процедур, которые позволяют обнаружить сигнал на фоне шумов с неизвестным распределением (случая непараметрической априорной неопределённости), сохраняя при этом постоянной вероятность ошибки первого рода. Произведена оценка эффективности некоторых из них, полученные результаты сопоставлены с характеристиками потенциально оптимального байесовского обнаружителя при том же объёме выборки.

В очередной статье исследовалась помехоустойчивость обнаружителя радиосигналов в каналах связи с априорно неизвестными характеристиками замираний с помощью имитационного статистического моделирования [14]. Данный подход можно использовать для оценки помехоустойчивости и других обнаружителей сигналов в радиотехнических системах.

Также во многих источниках исследуется помехоустойчивость различных обнаружителей, например в статье [15] исследуется помехоустойчивость рангового обнаружителя последовательности (пачки) импульсов с неизвестным законом флуктуаций. Закон распределения помехи также неизвестен. Предполагается последетекторная (некогерентная) обработка сигнала. Если сигнал есть, то считается, что он может находиться только в последнем из участков разрешения по дальность или азимуту. В качестве исследуемого взято ранговое правило Вилкоксона, основанное на сумме рангов.

В статье [16] приведен метод оценки вероятности правильного обнаружения Байесовского алгоритма при неточно известной плотности распределения вероятности. Получено выражение для оценки величины ошибки, зависящей от степени неточности априорно-известной плотности распределения. Приведены вероятностные характеристики для нескольких значений объема выборки.

Также было рассмотрено двухэтапное правило обнаружения некогерентной пачки импульсов в работе [17].

В статье [18] синтезирован ранговый обнаружитель импульсного сигнала в условиях априорной неопределенности мощности и функции плотности распределения вероятности шума. Получены вероятностные характеристики.

В [19] получены вероятностные характеристики обнаружителя радиосигнала с неизвестными параметрами в шумах неизвестной мощности. Правило обнаружения оптимально по критерию Неймана-Пирсона. Проведена оценка эффективности правила методом Монте-Карло.

В [20] при помощи имитационного моделирования получены графические характеристики мощности правила когерентного обнаружения узкополосного сигнала с неизвестной несущей частотой.

2. Алгоритмы обнаружения сигналов

2.1 Асимптотически оптимальные алгоритмы обнаружения сигналов

Оптимальным будем называть такой алгоритм обнаружения, который при фиксированной вероятности ложной тревоги обеспечивает при заданном размере выборки n минимальную вероятность P_ПС пропуска сигнала λ_ns (t) (критерий Неймана-Пирсона). Тогда асимптотически оптимальным (АО) будет такой алгоритм, если для любого другого алгоритма выполняется соотношение:

, (3)

где n - размер выборки,  - минимальная вероятность пропуска сигнала при обработке с помощью асимптотически оптимального алгоритма,  - минимальная вероятность пропуска сигнала при использовании любого иного алгоритма.

Основной идеей асимптотически оптимальных алгоритмов обнаружения сигналов на фоне помех является нахождение асимптотически достаточной статистики, распределение которой сводится к нормальному. Такая статистика существует при условии факторизации отношения правдоподобия, а, следовательно, при равенстве логарифма отношения правдоподобия сумме случайных величин.

Можно предположить, что если в известное оптимальное правило выбора решения для нормальных распределений подставить асимптотически достаточную статистику, то получится асимптотически оптимальный алгоритм обнаружения сигналов на фоне помех широкого класса, от распределения которых будет зависеть только устройство формирования достаточной статистики.

Рассмотрим асимптотические разложение логарифма правдоподобия.

Пусть  - независимая выборка из реализации x (t), где , . Проверяется гипотеза Н о том, что выборка однородная и принадлежит распределению помехи 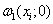против альтернативы К о том, что элемент выборки х_i принадлежит распределению  смеси детерминированного сигнала λ_п s (t) с помехой. Оптимальный алгоритм проверки обнаружения детерминированного сигнала на фоне стационарной независимой помехи состоит в сравнении с порогом отношения правдоподобия

 (4)

или (с учётом монотонности логарифмической функции логарифма) отношения правдоподобия

, (5)

который представляет при любом п достаточную статистику в задаче проверки статистических гипотез [1].

Синтез асимптотически оптимальных алгоритмов обнаружения сигналов на фоне помех как раз и основан на исследовании асимптотического разложения логарифма отношения правдоподобия при неограниченном увеличении размера выборки, а так же при стремлении амплитуды рассматриваемого сигнала λ_ns (t) к нулю и  ( 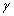- положительная константа).

алгоритм помеха асимптотический оптимальный

Cформулируем некоторые условия, которым должна удовлетворять плотность вероятности смеси сигнала с помехой. Обозначим через  параметр функции

, (6)

где s = s (t) - значение (нормированное) сигнала в произвольный момент времени. Потребуем, чтобы плотность вероятности  удовлетворяла следующим условиям:  непрерывна по  в точке равномерно по всем значениям x, не обращается в нуль в области возможных выборочных значений и допускает следующее разложение

, (7)

где  (8)

и  (9)

, (10)

причём для любого  всегда найдётся такое _0, что

.

При указанных условиях логарифм отношения правдоподобия допускает следующее асимптотическое разложение

, (11)

где W _{s -} мощность сигнала, а именно:

.

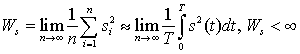Остаточный член  в полученном разложении (11) стремится к нулю по вероятности при  как при гипотезе H, так и при альтернативе к ней. Из (11) также видно, что асимптотические свойства логарифма отношения правдоподобия определяются в основном линейным членом, т.е. статистикой:

. (12)

Статистика (12) по центральной предельной теореме асимптотически нормальная, так как предполагается, что суммируемые величины независимы и что при достаточно большом числе n для реальных сигналов отношение дисперсии любого слагаемого  к дисперсии суммы  меньше любой произвольно малой величины.

Из (11) и (12) непосредственно следует, что при  статистика  отличается лишь постоянным множителем γ и слагаемым  от отношения правдоподобия, которое представляет достаточную статистику в рассматриваемой задаче обнаружения сигнала, следовательно,  является асимптотически достаточной. Тогда асимптотически оптимальное правило для обнаружения детерминированного сигнала λs (t) на фоне независимых помех с распределением  можно сформулировать так: решение о том, что сигнал есть, если

, (13)

а решение, что сигнала нет, если выполняется неравенство, противоположное (13). Значение порога определяется исходя из заданной вероятности ложной тревоги.

Структурную схему асимптотически оптимального обнаружителя детерминированного сигнала можно изобразить, как показано на рис.1. Она состоит из безынерционного нелинейного преобразователя выборки  в величину f (x); коррелятора, выполняющего операции перемножения сигнала на выходе нелинейного преобразователя и значений опорного сигнала и суммирования, и решающего устройства, на которое подаётся значение порога, при превышении которого выносится решение о наличии сигнала.

Рисунок 1 - Структурная схема асимптотически оптимального обнаружителя одиночного сигнала в случае когерентного приема сигнала

В случае некогерентной обработки согласно [1] появляется второй канал:

Рисунок 2 - Структурная схема асимптотически оптимального обнаружителя одиночного сигнала в случае некогерентной обработки

Для аддитивной нормальной помехи с нулевым средним и дисперсией σ², такой, что её распределение равно

, (14)

из (8) имеем

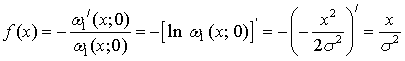. (15)

В этом случае алгоритм (13) совпадает с корреляционной обработкой, и решение о наличии сигнала принимается, когда выполняется нижеследующее условие

. (16)

В случае лапласовской аддитивной помехи со средней мощностью σ² и распределением

. (17)

Характеристика нелинейного преобразования выглядит так

, (18)

т.е. фактически является характеристикой идеального ограничителя.

Таким образом, если перед коррелятором поставить идеальный ограничитель, то получим обнаружитель детерминированного сигнала, причём асимптотически оптимальный для лапласовской помехи, а решение о наличии сигнала будет приниматься при выполнении условия

. (19)

Теперь предположим, что вместо распределения  имеем распределение , т.е. изменяются лишь параметры асимптотически нормального распределения.

Тогда среднее и дисперсия статистики (13) при гипотезе Н, когда выборка помехи принадлежит новому распределению

, (20)

, (21)

где .

Соответственно при альтернативе К, когда выборка x_i принадлежит распределению , среднее значение статистики записывается как

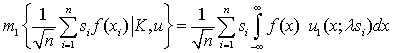 (22), и при

, (23)

где , (24)

тогда имеем

 (25)

Соответственно дисперсия статистики (13) при альтернативе К и тех же условиях:

, (26)

т.е. определяется согласно (21). Асимптотически оптимальный алгоритм обнаружения детерминированного сигнала на фоне помех с распределением , получаем из (13) подстановкой g (x) (24) вместо f (x), а именно

. (27)

Тогда параметры данной статистики равны:

, (28)

. (29)

Чтобы охарактеризовать устойчивость алгоритма (14), найдём его коэффициент асимптотической относительной эффективности ρ, когда действует помеха с распределением  по отношению к алгоритму (27). ρ можно определить как произведение возведённых в квадрат отношений среднего значения и дисперсии для рассматриваемого алгоритма, тогда в данном случае имеем:

. (30)

Если рассматриваемые в алгоритмах распределения помех симметричны относительно нуля, тогда выполняется (28) и

. (31)

Рассмотрим несколько примеров.

Если , то алгоритм совпадает с линейным алгоритмом, оптимальным при нормальной аддитивной помехе с

. (32)

Пусть линейный алгоритм используется для обнаружения детерминированного сигнала на фоне аддитивной помехи с распределением Лапласа с дисперсией [см. (17)]:

, (33)

и имеем , тогда по формуле (31):

. (34)

Видно, что асимптотическая эффективность линейного оптимального при нормальной помехе алгоритма снижается в два раза при его использовании для обнаружения сигнала на фоне лапласовской помехи.

Если 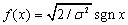, то алгоритм совпадает с асимптотически оптимальным алгоритмом обнаружения детерминированного сигнала на фоне аддитивной лапласовской помехи. Пусть этот алгоритм используется для обнаружения детерминированного сигнала на фоне аддитивной нормальной помехи с дисперсией σ², тогда и по формуле (31) имеем:

. (35)

2.2 Ранговые алгоритмы обнаружения сигналов на фоне независимых помех

В случае ранговых и знаково-ранговых алгоритмов обнаружения сигналов при конечных размерах выборки синтезу оптимальных по критерию Неймана-Пирсона алгоритмов обнаружения препятствуют непреодолимые математические трудности, что является причиной фактически эвристического выбора того или иного рангового метода, избежать такого выбора помогает асимптотический подход.

При определённых условиях, а именно при ограничениях на структуру сигнала и помехи, существуют асимптотически наиболее эффективные ранговые алгоритмы обнаружения сигналов, эквивалентные по характеристикам обнаружения неранговым алгоритмам, оптимальным по критерию Неймана-Пирсона.

Введём случайную величину

, (36)

где F_{1 -} интегральная функция распределения, которому принадлежит выборка x_i. Она распределена равномерно на интервале (0, 1). АО ранговые алгоритмы обнаружения сигналов на фоне независимых помех можно получить из АО неранговых алгоритмов заменой

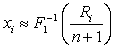, (37)

где R_i - ранг элемента x_i выборки размера n.

Используя это, из (14) можно получить асимптотически оптимальное ранговое правило обнаружение детерминированного сигнала с помощью замены x_i на :

. (38)

Сформулируем данное правило для различных типов помех.

Для аддитивной помехи согласно (16) имеем:

. (39)

В случае нормальной помехи

. (40)

где  - функция, обратная интегральной функции нормального распределения (интеграла Лапласа), таким образом, правило формулируется:

. (41)

При лапласовской помехе  можно получить

, (42)

соответственно правило преобразуется к виду:

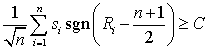. (43)

Устойчивость же АО ранговых алгоритмов так же можно охарактеризовать коэффициентом относительной асимптотической эффективности. Если при обнаружении детерминированного сигнала на фоне помехи с распределением u₁ (x; 0) используется АО ранговый алгоритм, рассчитанный на помеху с распределением ω₁ (x; 0), то получим, что указанный коэффициент эффективности рангового алгоритма по "чужой" помехе по отношению к асимптотически оптимальному равен:

, (44)

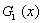где  и  - функции, обратные интегральным функциям распределения  и , производные которых равны ω₁ (x; 0) и u₁ (x; 0) соответственно.

Формула (44) симметрична относительно распределений ω₁ (x; 0) и u₁ (x; 0), что говорит о равенстве относительной эффективности двух алгоритмов: алгоритма, настроенного на помеху ω₁ (x; 0), при использовании в помехе u₁ (x; 0) и алгоритма, настроенного на помеху u₁ (x; 0), при использовании в помехе ω₁ (x; 0).

Для алгоритма, работающего при лапласовской помехе, при использовании в нормальной помехе получим

. (45)

При сравнении (45) с (34) и (35) можно сделать вывод о том, что относительные эффективности АО нерангового и рангового алгоритмов, настроенных на лапласовскую помеху при использовании их на фоне нормальной помехе, равны и составляют 2/π. Относительная эффективность АО рангового алгоритма, настроенного на нормальную помеху, при его использовании в лапласовской помехе в 2,5 раза больше относительной эффективности АО нерангового алгоритма, настроенного на нормальную помеху, при его использовании в лапласовской помехе. Общее выражение коэффициента относительной эффективности АО рангового по отношению к неранговому алгоритму, при условии, что эти алгоритмы настроены на помеху ω₁ (x; 0), а используются при помехе u₁ (x; 0), имеет вид:

. (46)

2.3 Асимптотически оптимальный алгоритм некогерентного приема узкополосного сигнала со случайной фазой

Рассматривается задача обнаружения узкополосного сигнала на фоне помех с помощью АО алгоритма. Сигнал имеет вид [3]:

, (47)

Слагаемые, содержащие неизвестную начальную фазу:

Слагаемые, содержащие несущую, фазовую и амплитудную модуляцию:

Таким образом, получаем следующий вид сигнала, который будет смоделирован в ходе исследования:

. (48)

Для такого сигнала векторная статистика является двумерной и представляет собой:

 (49)

,

где  - линейное преобразование случайного процесса , представляющего собой смесь сигнала и шума.

Приняв распределение случайной фазы равномерным на интервале , получаем общую для двух слагаемых статистику:

 (50)

Решение в пользу гипотезы о том, что на входе обнаружителя сигнал, принимается в случае превышения статистикой порога:

 (51)

Структурная схема обнаружителя представлена на рисунке 3.

Рисунок 3 - Структурная схема асимптотически оптимального обнаружителя узкополосного сигнала

2.4 Последетекторный асимптотически оптимальный алгоритм обнаружения модулированного сигнала со случайной фазой (амплитудный метод)

Рассмотрим случай обнаружения, в котором до оптимальной обработки наблюдаемый узкополосный случайный процесс детектируется, то есть выделяется его огибающая. Пусть 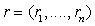 - выборка огибающей наблюдаемого процесса, представляющего собой либо огибающую стационарной случайной узкополосной помехи, либо огибающую смеси этой помехи с сигналом (47). Обозначим через  функцию распределения огибающей помехи через  функцию распределения огибающей смеси сигнала с помехой.

Последетекторный (по огибающей) асимптотически оптимальный алгоритм обнаружения сигнала принимает следующий вид, согласно [3]:

 (52)

При этом нелинейное преобразование имеет вид:

 (53)

3 Выделение огибающей узкополосного случайного процесса. Квадратурный демодулятор

Удобным инструментом для анализа узкополосных сигналов является комплексная огибающая сигнала [6].

В общем случае (в зависимости от вида модуляции) у сигнала s (t) может изменяться как амплитуда, так и начальная фаза:

(t) = A (t) ∙cos (ω₀∙t +φ (t)) (54)

(t) - амплитудная огибающая (закон, по которому изменяется амплитуда); φ (t) - фазовая функция закон (закон, по которому изменяется начальная фаза). Весь аргумент функции cos называется полной фазой сигнала ψ (t) = ω₀∙t + φ (t), тогда

(t) = A (t) ∙cos (ψ (t)) (55)

Сигнал (1) можно представить как вещественную часть комплексной функции, заменив косинус комплексной экспонентой.

(t) =Re (A (t) ·exp (j·ψ (t))) (56)

По формуле Эйлера

(j·ψ (t))) = cos (ψ (t)) + j· sin (ψ (t)), следовательно Re (exp (j·ψ (t))) = cos (ψ (t)).

Проанализируем функцию A (t) ·exp (ψ (t)).

(t) ·exp (j·ψ (t)) = A (t) ·exp (j· (ω₀∙t +φ (t))) = A (t) ·exp (j·ω₀∙t) · exp (j·φ (t)) (57)

Множитель exp (j·ω₀∙t) представляет собой немодулированное несущее колебание и является быстроменяющимся, а A (t) ·exp (j·φ (t)) меняется, как правило, значительно медленнее и содержит информацию об амплитудной огибающей и начальной фазе одновременно. Этот медленноменяющийся множитель и называется комплексной огибающей сигнала:

 (58)

Комплексная огибающая содержит всю необходимую информацию для декодирования сигнала и вычисления его мощностных и фазовых характеристик.

Представим комплексную огибающую в косинусно-синусной форме, воспользовавшись формулой Эйлера, тогда:

=A (t) ·cos (φ (t)) + A (t) ·j·sin (φ (t)) =i (t) + j∙q (t) (59)

(t) =A (t) ·cos (φ (t)) - синфазная (косинусная) компонента комплексной огибающей; q (t) =A (t) ·sin (φ (t)) - квадратурная (синусная) компонента комплексной огибающей.

Тогда A (t) ·exp (j·ψ (t)) можно представить в виде

(t) ·exp (j·ψ (t)) = (i (t) +j∙q (t)) ·exp (j·ω₀∙t) =

= (i (t) +j∙q (t)) ∙ (cos (ω₀∙t) + j∙sin (ω₀∙t)) =

=i (t) ∙ cos (ω₀∙t) +i (t) ∙j∙sin (ω₀∙t) + j∙q (t) ∙cos (ω₀∙t) + j∙q (t) ∙j∙sin (ω₀∙t) =

=i (t) ∙ cos (ω₀∙t) - q (t) ∙ sin (ω₀∙t) +j∙ (i (t) ∙sin (ω₀∙t) +q (t) ∙cos (ω₀∙t)) (60)

s (t) = i (t) ∙cos (ω₀∙t) - q (t) ∙sin (ω₀∙t) (61)

На основе формулы (61) можно построить векторный модулятор, с помощью которого можно получить любые виды модуляции. При этом амплитудная огибающая A (t) =, фазовая функция φ (t) =arctan (q (t) /i (t)) На рисунке 4 представлена функциональная схема векторного модулятора.

Рисунок 4 - Функциональная схема векторного модулятора

Так как cos (ω₀∙t + π/2) =-sin (ω₀∙t), то формулу можно переписать в виде s (t) = i (t) ∙cos (ω₀∙t) +q (t) ∙cos (ω₀∙t +π/2). Таким образом, в схему на рисунке 5 нужно ввести фазовращатель на угол π/2.

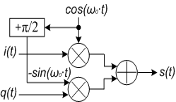
Рисунок 5 - Функциональная схема векторного модулятора с фазовращателем

Для выделения из сигнала комплексной огибающей используется процедура гетеродинирования. Входной ВЧ-сигнал s (t) = A (t) ∙cos (ω₀∙t +φ (t)) умножается на колебание двух генераторов (гетеродинов) с частотой ω₀, сдвинутых по фазе друг относительно друга на угол π/2 cos (ω₀∙t) и - sin (ω₀∙t).

(t) ∙cos (ω₀∙t) = A (t) ∙cos (ω₀∙t +φ (t)) ∙cos (ω₀∙t) =

,5∙ A (t) ∙cos (φ (t)) + 0,5∙ A (t) ∙cos (2ω₀∙t +φ (t)) = (62)

0,5∙i (t) + 0,5∙ A (t) ∙cos (2ω₀∙t +φ (t))(t) ∙ (-sin (ω₀∙t)) = - A (t) ∙cos (ω₀∙t +φ (t)) ∙sin (ω₀∙t) =

,5∙ A (t) ∙sin (φ (t)) - 0,5∙ A (t) ∙sin (2ω₀∙t+φ (t)) = (63)

0,5∙q (t) - 0,5∙ A (t) ∙sin (2ω₀∙t+φ (t))

Из формул (62) и (63) видно, что результаты умножений содержат две составляющие - низкочастотную 0,5∙i (t) и 0,5∙q (t), которые являются действительной и мнимой частями комплексной огибающей и высокочастотную 0,5∙ A (t) ∙cos (2ω₀∙t +φ (t)) и - 0,5∙ A (t) ∙sin (2ω₀∙t+φ (t)), которые могут быть убраны фильтром низких частот (ФНЧ). На рисунках представлены схемы квадратурного демодулятора с фазовращателем и без фазовращателя.

Рисунок 6 - Функциональная схема квадратурного демодулятора

Рисунок 7 - Функциональная схема квадратурного демодулятора с фазовращателем

Таким образом, структурная схема последетекторного обнаружителя узкополосного сигнала принимает вид:

Рисунок 8 - Структурная схема последетекторного обнаружителя узкополосного сигнала

4. Моделирование алгоритмов

4.1 АО и ранговые алгоритмы

Как было показано выше [3], асимптотически оптимальное правило для обнаружения детерминированного узкоплосного сигнала λs (t) на фоне независимых помех с распределением  можно сформулировать так: принимается решение о присутствии сигнала при превышении статистикой порога, т.е. при выполнении неравенства

 (64)

и решение об отсутствии сигнала в противоположном случае.

Характер нелинейного преобразования для случая присутствия аддитивной помехи имеет следующий вид:

. (65)

Подставляя плотность распределения помехи (1) в данное выражение, приходим к виду преобразования, зависящему от параметра  плотности распределения помехи:

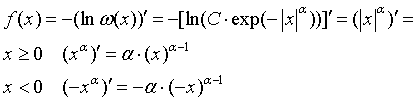
. (66)

Подставляя значения  в выражение (66), получаем нелинейное преобразование, обеспечивающее статистику (64) асимптотической оптимальностью именно для данного значения плотности распределения помехи.

Таким образом, для  (лапласовская помеха) оптимальным является знаковый алгоритм:

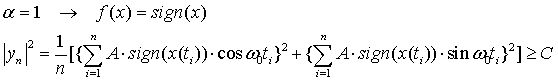, (67)

для  (нормальное распределение помехи) оптимальным является

линейный алгоритм:

. (68)

Дополнительно были получены выражения для нелинейного преобразования, оптимальные при значениях :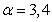

. (69)

Задача обнаружения сигнала при помощи ранговых алгоритмов подразумевает рассмотрение следующего правила:

. (70)

Аналогично случаю (64) решение о присутствии сигнала выносится при выполнении данного неравенства.

Нелинейное преобразование при аддитивной помехе имеет вид, схожий с (65):

, (71)

где  - функция, обратная интегральной функции распределения рассматриваемой выборки. Аналогично рассмотренному выше примеру при подстановке выражения для плотности распределения помехи (1) получается следующий общий вид преобразования:

. (72)

При дальнейшей подстановке значений  приходим к выражениям для медианного алгоритма обнаружения (оптимален при лапласовской помехе, ):

, (73)

и для алгоритма Ван-дер-Вардена (оптимален при нормальной помехе, т.е. ):

 (74)

Полученные выше алгоритмы также были исследованы при последетекторной обработке. В силу того, что они не являются оптимальными, так как нелинейное преобразование (65) зависит не от распределения случайного процесса, а от распределения огибающей этого процесса, мощностные характеристики обнаружителей, построенных на этих алгоритмах, проигрывают случаю додетекторной обработки.

4.2 Моделирование фильтра низкой частоты

Как было показано выше, для реализации выделения огибающей необходим ФНЧ. С помощью пакета FdaTool в среде Matlab был сформирован массив коэффициентов фильтра:

Рисунок 9 - Моделирование ФНЧ в программе FdaTool

Следующим этапом является свертка полученных коэффициентов и выборки реализации случайного процесса, результатом которой и будет отфильтрованная НЧ составляющая сигнала. После сложения и выделения квадратного корня имеем огибающую (показана на рисунке красным цветом):

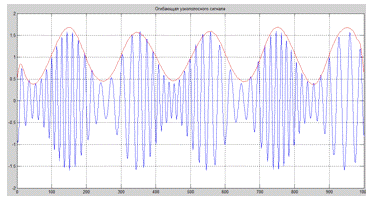
Рисунок 10 - Огибающая узкополосного сигнала

4.3 Алгоритм моделирования обнаружителя узкополосного сигнала

Рисунок 11 - Блок-схема моделирования некогерентного алгоритма обнаружения

4.4 Алгоритм моделирования последетекторного обнаружителя

Рисунок 12 - Блок-схема моделирования последетекторного алгоритма обнаружения

4.5 Моделирование помехи

Для осуществления моделирования необходимо создать шумовую выборку, плотность распределения вероятности которой подчинялась бы выражению (1). В качестве константы в выражении (1) выступает величина , полученная путем использования свойства плотности распределения:

. (75)

В итоге окончательное выражение для плотности распределения помехи примет вид:

,  [1; 4]. (76)

Исходя из полученного выражения, получается интегральная функция распределения величины x:

 

, (77)

где  - неполная гамма-функция.

Далее, исходя из свойства о том, что если случайную величину , распределенную равномерно на интервале (0, 1), подвергнуть преобразованию по закону , то восстанавливается реализация случайной величины, распределенной по закону (77) с плотностью распределения . Именно таким образом моделируется шумовая выборка для различных значений параметра α.

Следует заметить, что дисперсия указанной помехи равна 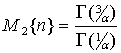. Для того, чтоб сравнивать эффективность работы алгоритмов при воздействии различных помех, эти помехи должны иметь одинаковые дисперсии. Поэтому случайную величину необходимо умножать на коэффициент, равный . Данная нормировка позволяет получить дисперсию:

. (78)

4.6 Отношение сигнал/шум

В качестве характеристики изучаемых алгоритмов выступает зависимость вероятности обнаружения сигнала от отношения сигнал/шум. В случае аналогового обнаружения данный параметр представляет собой:

, (79)

где  - амплитуда сигнала,  - энергия сигнала,  - спектральная плотность средней мощности шума. В нашем случае производится дискретная обработка, поэтому, сохраняя аналогию с выражением (79) получаем выражение для отношения сигнал/шум:

, (80)

при условии равенства СКО помехи единице.

Непосредственно на характеристиках параметр  преобразован для большей наглядности к виду , что позволяет рассматривать отношение сигнал/шум в децибелах.

5. Рабочие характеристики алгоритмов

5.1 Додетекторное обнаружение

Рисунок 13 - Рабочая характеристика АО знакового алгоритма

Таблица 1. Результаты моделирования АО знакового алгоритма обнаружения

Знаковый алгоритм
h, дБ	α=1	α=2	α=3	α=4
-3,98	0,005	0,001	0,003	0,004
2,04	0,019	0,018	0,008	0,011
5,56	0,147	0,053	0,047	0,038
8,06	0,396	0, 191	0,114	0,089
10,00	0,682	0,45	0,298	0, 195
11,58	0,9	0,706	0,515	0,432
12,92	0,972	0,745	0,655
14,08	0,997	0,976	0,901	0,849
15,11	1	0,996	0,97	0,945
16,02	1	0,999	0,993	0,983
16,85	1	1	1	0,996
17,60	1	1	1	1
18,30	1	1	1	1
18,94	1	1	1	1
19,54	1	1	1	1

Рисунок 14 - Рабочая характеристика АО линейного алгоритма

Таблица 2. Результаты моделирования АО линейного алгоритма обнаружения

Линейный алгоритм
h, дБ	α=1	α=2	α=3	α=4
-3,98	0,004	0,007	0,009	0,006
2,04	0,021	0,037	0,042	0,052
5,56	0,048	0,168	0,222	0,171
8,06	0,155	0,448	0,52	0,515
10,00	0,34	0,776	0,797	0,824
11,58	0,596	0,966	0,965	0,961
12,92	0,791	0,994	0,999	0,995
14,08	0,931	1	1	1
15,11	0,973	1	1	1
16,02	0,991	1	1	1
16,85	1	1	1	1
17,60	1	1	1	1
18,30	1	1	1	1
18,94	1	1	1	1
19,54	1	1	1	1

Рисунок 15 - Рабочая характеристика АО рангового медианного алгоритма

Таблица 3. Результаты моделирования АО рангового медианного алгоритма обнаружения

Медианный алгоритм
h, дБ	α=1	α=2	α=3	α=4
-3,98	0,004	0,003	0,009	0,001
2,04	0,033	0,018	0,026	0,01
5,56	0,145	0,073	0,078	0,04
8,06	0,394	0,229	0,188	0,097
10,00	0,697	0,488	0,369	0,226
11,58	0,905	0,732	0,625	0,463
12,92	0,974	0,917	0,821	0,676
14,08	0,996	0,983	0,951	0,856
15,11	1	0,998	0,982	0,952
16,02	1	1	0,997	0,99
16,85	1	1	1	0,999
17,60	1	1	1	0,999
18,30	1	1	1	1
18,94	1	1	1	1
19,54	1	1	1	1

Рисунок 16 - Рабочая характеристика АО рангового алгоритма Ван-дер-Вардена

Таблица 4. Результаты моделирования АО рангового алгоритма обнаружения Ван-дер-Вардена

Алгоритм Ван-дер-Вардена
h, дБ	α=1	α=2	α=3	α=4
-3,98	0,004	0,001	0,006	0,011
2,04	0,008	0,037	0,058	0,039
5,56	0,064	0,164	0, 19	0, 202
8,06	0,169	0,456	0,536	0,546
10,00	0,435	0,775	0,855	0,849
11,58	0,709	0,954	0,966	0,972
12,92	0,877	0,993	0,998	0,997
14,08	0,965	0,999	1	1
15,11	0,999	1	1	1
16,02	1	1	1	1
16,85	1	1	1	1
17,60	1	1	1	1
18,30	1	1	1	1
18,94	1	1	1	1
19,54	1	1	1	1

5.2 Последетекторное обнаружение

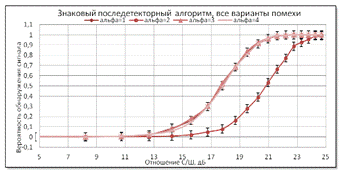
Рисунок 17 - Рабочая характеристика знакового алгоритма, последетекторный прием

Таблица 5. Результаты моделирования знакового алгоритма

Знаковый алгоритм
h, дБ	α=1	α=2	α=3	α=4
4,70	0,001	0	0,004	0,001
8,22	0,003	0	0,002	0
10,72	0,005	0,003	0,007	0,008
12,66	0,024	0,004	0,023	0,026
14,24	0,087	0,009	0,077	0,059
15,58	0,164	0,022	0,178	0,144
16,74	0,297	0,049	0,301	0,295
17,76	0,501	0,078	0,525	0,485
18,68	0,684	0,162	0,685	0,68
19,51	0,831	0,835	0,805
20,26	0,91	0,389	0,921	0,909
20,96	0,96	0,532	0,964	0,963
21,60	0,989	0,663	0,989	0,992
22, 20	0,997	0,772	0,993	0,992
22,76	1	0,887	1	0,997
23,29	1	0,926	0,999	0,999
23,78	1	0,955	0,999	1
24,25	1	0,988	1	1
24,70	1	0,99	1	1

Рисунок 18 - Рабочая характеристика линейного алгоритма, последетекторный прием

Таблица 6. Результаты моделирования линейного алгоритма

Линейный алгоритм
h, дБ	α=1	α=2	α=3	α=4
4,70	0,003	0,001	0	0,003
8,22	0,003	0,016	0,014	0,016
10,72	0,008	0,028	0,037	0,052
12,66	0,018	0,121	0,119	0,145
14,24	0,032	0,244	0,284	0,292
15,58	0,092	0,441	0,492	0,539
16,74	0,189	0,711	0,738	0,736
17,76	0,314	0,866	0,897	0,92
18,68	0,459	0,958	0,967	0,972
19,51	0,615	0,988	0,99	0,99
20,26	0,785	0,998	0,999	1
20,96	0,868	0,999	0,999	1
21,60	0,932	1	1	1
22, 20	0,966	1	1	1
22,76	0,988	1	1	1
23,29	0,997	1	1	1
23,78	1	1	1	1
24,25	0,999	1	1	1
24,70	1	1	1	1

Рисунок 19 - Рабочая характеристика медианного алгоритма, последетекторный прием

Таблица 7. Результаты моделирования линейного алгоритма

Медианный алгоритм
h, дБ	α=1	α=2	α=3	α=4
4,70	0,001	0	0,005	0
8,22	0,005	0,008	0,02	0,001
10,72	0,018	0,005	0,011	0,012
12,66	0,044	0,008	0,025	0,025
14,24	0,101	0,018	0,091	0,063
15,58	0,212	0,048	0,175	0,16
16,74	0,402	0,084	0,312	0,303
17,76	0,572	0,18	0,53	0,489
18,68	0,74	0,271	0,688	0,7
19,51	0,868	0,397	0,843	0,806
20,26	0,948	0,545	0,931	0,92
20,96	0,984	0,699	0,972	0,971
21,60	0,991	0,781	0,993	0,995
22, 20	0,999	0,86	0,999	0,997
22,76	0,999	0,939	1	0,999
23,29	0,999	0,962	0,999	0,999
23,78	1	0,979	0,999	1
24,25	1	0,996	1	1
24,70	1	0,999	1	1

Рисунок 20 - Рабочая характеристика алгоритма Ван-дер-Вардена, последетекторный прием

Таблица 8. Результаты моделирования алгоритма Ван-дер-Вардена

Алгоритм Ван-дер-Вардена
h, дБ	α=1	α=2	α=3	α=4
4,70	0,002	0,001	0	0
8,22	0,002	0,01	0,005	0,01
10,72	0,003	0,03	0,025	0,032
12,66	0,006	0,049	0,048	0,052
14,24	0,02	0,143	0,135	0,141
15,58	0,034	0,287	0,284	0,288
16,74	0,07	0,471	0,473	0,474
17,76	0,144	0,666	0,652	0,661
18,68	0,248	0,842	0,835	0,844
19,51	0,368	0,941	0,928	0,937
20,26	0,509	0,985	0,969	0,983
20,96	0,65	0,992	0,975	0,99
21,60	0,753	0,999	0,999	0,999
22, 20	0,862	1	1	1
22,76	0,936	1	1	1
23,29	0,966	1	1	1
23,78	0,991	1	1	1
24,25	1	1	1
24,70	1	1	1	1

6. Коэффициент относительной асимптотической эффективности

Нахождение коэффициента асимптотической относительной эффективности строится на сравнении работы алгоритма, настроенного на помеху с показателем экспоненты, равным  при воздействии шума с плотностью распределения  и алгоритма, оптимального для этой помехи. В случае АО алгоритмов удалось найти выражение, явно зависящее от данных параметров помехи. Напомним, что в общем виде КАОЭ считается как

. (81)

Подставим выражения для нелинейностей и помех:

, (82)

Аналогичным образом как показано в (82) получается:

. (83)

Далее числитель:

. (84)

Наконец, итоговая формула, для наглядности выраженная в децибелах, примет вид:

. (85)

На основании полученных экспериментальных данных можно вычислить коэффициент асимптотической относительной эффективности одного алгоритма обнаружения по отношению к другому следующим образом:

, (86)

где  и  - математическое ожидание и среднеквадратическое отклонение первой статистики;  и  - среднее и среднеквадратическое отклонение второй статистики при равных помеховых условиях.

Таблица 9. Результаты моделирования алгоритмов

Алгоритм	Параметр распределения помехи α	Мат. ожидание статистики	СКО статистики
Знаковый	α=1	23641,38	5873,68
	α=2	20868,78	5478,72
	α=3	16252,60	4839,14
	α=4	14594,38	4598,56
Линейный	α=1	35123,09	10447,18
	α=2	33985,60	7221,62
	α=3	34052,11	7318,67
	α=4	34125,63	7265, 19
Медианный	α=1	23627,74	5928,53
	α=2	20843, 20	5424,14
	α=3	16279,87	4893,62
	α=4	14599,13	4613,74
Ван-дер-Вардена	α=1	19709,45	5276,77
	α=2	30243,09	6154,69
	α=3	30884,66	6122,28
	α=4	31853,60	6096,02

КАОЭ знакового алгоритма, оптимального при лапласовской помехе по отношению к линейному алгоритму, оптимальному при нормальной помехе, равен  (помеха нормальная). То есть при нормальной помехе знаковый обнаружитель (при больших размерах выборки и слабом сигнале) менее эффективен, чем оптимальный для нормальной помехи линейный обнаружитель. Теоретически согласно (85) проигрыш составляет  дБ.

Рисунок 21 - Характеристика обнаружения знакового и линейного алгоритмов на фоне нормальной помехи

Если в качестве шума для этих двух алгоритмов рассматривать лапласовскую помеху, то КАОЭ линейного алгоритма при С/Ш 13 дБ составляет , при расчетном теоретическом значении - 3,01 дБ (проигрыш в два раза).

Рисунок 22 - Характеристика обнаружения знакового и линейного алгоритмов на фоне лапласовской помехи

Сравнивая пару АО ранговых алгоритмов, оптимальных для тех же помех, получаем следующие характеристики:

Рисунок 23 - Характеристика обнаружения медианного и алгоритма Ван-дер-Вардена на фоне нормальной помехи

Рисунок 24 - Характеристика обнаружения медианного и алгоритма Ван-дер-Вардена на фоне лапласовской помехи

Поскольку моделируются ранговые алгоритмы, теоретическое значение КАОЭ для обоих случаев в силу симметричности формулы (44) относительно распределений ω₁ (x; 0) и u₁ (x; 0) одинаково и равно - 1,95 дБ. Практические результаты составили:  проигрывает медианный алгоритм при обнаружении сигнала на фоне нормальной помехи и  проигрывает алгоритм Ван-дер-Вардена в обстановке лапласовской помехи.

Сравнивая АО неранговые алгоритмы с АО ранговыми при условии настройки на одну и ту же помеху, можно подтвердить, что при выполнении асимптотических условий их характеристики стремятся совпасть:

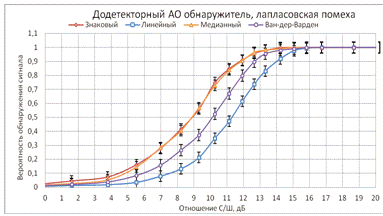
Рисунок 25 - Характеристика обнаружителей на фоне лапласовской помехи

Медианный и знаковый алгоритмы практически идентичны, Ван-дер-Вардена несколько выигрывает линейный алгоритм. Данное явление можно обусловить конечностью членов выборки, которая в идеальном случае стремится к бесконечности. Также это показывает большую устойчивость алгоритма Ван-дер-Вардена к изменению помеховой обстановки.

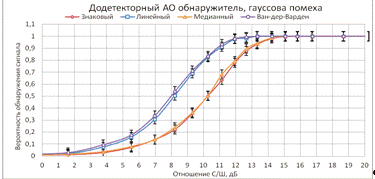
Рисунок 26 - Характеристика обнаружителей на фоне гауссовой помехи

В данном случае ситуация аналогична для другой пары алгоритмов - медианный более устойчив нежели знаковый алгоритм при гауссовой помехе.

Рисунок 27 - Характеристика обнаружителей на фоне помехи при α=3

Рисунок 28 - Характеристика обнаружителей на фоне помехи при α=4

При работе в условиях помех с показателями α=3,4 ранговые алгоритмы демонстрируют большую устойчивость по сравнению с неранговыми, хотя их характеристики стремятся совпасть.

Таблица 10. Сравнительная таблица теоретического и практического значений КАОЭ

Алгоритм	Коэффициент АОЭ
	Теоретическое значение, дБ (раз)	Рассчитанное значение, дБ (раз)
Знаковый	-1,96 (0,636)	-1,86 (0,650)
Линейный	-3,01 (0,5)	-2,03 (0,626)
Медианный	-1,95 (0,638)	-1,98 (0,633)
Ван-дер-Вардена	-1,95 (0,638)	-1,49 (0,708)

Помимо вышерассмотренных КАОЭ, необходимо рассмотреть эффективность работы алгоритмов при условии последетекторной обработки.

Таблица 11. Сравнительная таблица додетекторного и последетекторного приема

Алгоритм	Обнаружитель	Мат. ожидание статистики	СКО статистики	КАОЭ
				раз	дБ
Знаковый	Додетекторный	52612,73857	9812,773104	0,166	-7,80
	Последетекторный	213,764728	97,85355006
Линейный	Додетекторный	49154,88	9713,08	0,239	-6,21
	Последетекторный	34,91464884	14,10228235
Медианный	Додетекторный	127922,1887	24144,55227	0,152	-8, 19
	Последетекторный	187,3223265	90,76610516
Ван-дер-Вардена	Додетекторный	10990,1788	4862,569093	0,182	-7,40
	Последетекторный	331,7973395	86,5965403

Данные значения КАОЭ получаются путем сравнения работы алгоритмов при настройке на "свою" помеху с работой в последетекторных условиях.

Как уже отмечалось ранее, обнаружение по огибающей проигрывает додетекторному случаю, поскольку рассматриваемые в работе алгоритмы не являются АО. Этот проигрыш весьма велик, более 6 дБ, однако все-таки алгоритмы работоспособны.

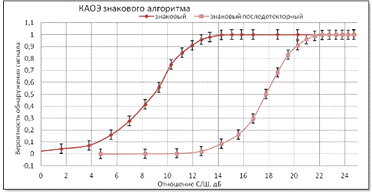
Рисунок 29 - Характеристика обнаружения знакового и последетекторного знакового алгоритмов на фоне лапласовской помехи

Рисунок 30 - Характеристика обнаружения линейного и последетекторного линейного алгоритмов на фоне гауссовской помехи

Рисунок 31 - Характеристика обнаружения медианного и последетекторного медианного алгоритмов на фоне лапласовской помехи

Рисунок 32 - Характеристика обнаружения алгоритмов последетекторного и Ван-дер-Вардена на фоне гауссовской помехи

Примечателен также тот факт, что сохраняется тенденция лучшей работы обнаружителя при настройке на "свою помеху", например знаковый алгоритм выигрывает при лапласовской помехе у себя же на фоне гауссова шума.

Рисунок 33 - Характеристика обнаружителей на фоне лапласовской помехи

Также рассмотрены различные вероятности ложной тревоги, влияющие непосредственно на порог принятия решения в каждом из алгоритмов. С уменьшением вероятности ложной тревоги возрастает порог, что приводит к смещению характеристик в направлении большего отношения С/Ш:

7. Доверительные интервалы

Полученные результаты различаются при каждом очередном испытании, поэтому следует рассмотреть доверительные интервалы для определенных выше значений вероятности обнаружения сигнала.

Для произвольного заданного значения 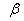укажем такое 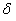, что

 (87)

где  - истинное значение оцениваемого параметр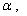а а  - статистическая оценка.

Чем меньше для заданного величина 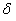, тем оценка точнее. Имеем:

. (88)

Таким образом, величина характеризует вероятность, с которой истинное значение  окажется внутри интервала 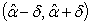со случайными концами. Такой интервал называется доверительным интервалом, а вероятность  - доверительной вероятностью.

Приведенная оценка значения  параметра называется интервальной оценкой.

Итак, для конкретного значения  (в нашем случае это математическое ожидание статистики) имеем границы доверительного интервала

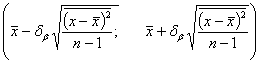. (89)

В случае нахождения доверительного интервала для вероятности правильного обнаружения сигнала используется иная формула [4]:

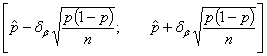 (90)

Рассмотрены точки для каждого из рассмотренных алгоритмов. Величина в графе "Мат. ожидание статистики" является автоматически средней, так как моделирование предполагает большое число испытаний. Значение  взято из таблицы t-распределения и равно 2,58 для доверительной вероятности 0,99 [4].

Таблица 12. Доверительные интервалы для оценки полученных данных

Алгоритм	Параметр распределения помехи α	Длина доверительного интервала
		Мат. ожидание статистики	Вероятность обнаружения
Знаковый	α=1	958,9	0,076
	α=2	894,4	0,081
	α=3	790,0	0,075
	α=4	750,7	0,065
Линейный	α=1	1705,6	0,077
	α=2	1179,0	0,068
	α=3	1194,8	0,066
	α=4	1186,1	0,062
Медианный	α=1	967,9	0,075
	α=2	885,5	0,082
	α=3	798,9	0,079
	α=4	753,2	0,068
Ван-дер-Вардена	α=1	861,5	0,081
	α=2	1004,8	0,068
	α=3	999,5	0,057
	α=4	995,2	0,058

8. Датчик случайных величин. Тестирование по критерию Хи-квадрат

Рассмотрим задачу по проверке близости теоретической и эмпирической функций распределения для дискретного распределения [7]. При этом закон распределения задаётся набором вероятностей р₁,., р_k, а гипотеза сводится к тому, что эти вероятности приняли определенные значения. То есть гипотеза Н₀: р₁ = р₁₀, р₂ = р₂₀,., р_k = р_k0. Для решения такой задачи используется теорема Пирсона.

Теорема Пирсона

Пусть n - число независимых повторений некоего опыта, который заканчивается одним из k (k - натуральное число) элементарных исходов А₁,., А_k, причём вероятности этих исходов - р₁,., р_k, p₁ +. + р_k = 1. Обозначим через m₁,.,m_k (m₁ +. + m_k = n) то количество опытов, которые закончились исходами А₁,., А_k. Введем случайную величину

. (91)

Тогда при неограниченном росте n → ∞ случайная величина  асимптотически подчиняется распределению  с (k - 1) степенями свободы.

Для проверки гипотезы Н0 о том, что вероятности р1,…, рk приняли определенные значения Н₀: р₁ = р₁₀, р₂ = р₂₀,., р_k = р_k0, рассмотрим следующую статистику: Статистика

 (92)

называется статистикой хи-квадрат Пирсона для простой гипотезы.

Фактически величина XІ/n представляет собой квадрат некоего расстояния между двумя k-мерными векторами: вектором наблюдаемых относительных частот (m_i/n) и вектором предсказанных ненаблюдаемых вероятностей (р_i0). От евклидового расстояния это расстояние отличается тем, что разные координаты входят в него с разными весами. Если верна гипотеза Н₀, то асимптотическое поведение XІ при n → ∞ указывает теорема Пирсона. Чтобы понять, что происходит, когда Н₀ неверна, заметим, что по закону больших чисел (m_i/n) → р_i при n → ∞ для всех допустимых i = 1,.,k. Поэтому при n → ∞:

. (93)

Если гипотеза неверна, то XІ → ∞ при n → ∞. Значит, гипотеза Н₀ должна быть отвергнута, если полученное в опыте значение XІ слишком велико. Термин "слишком велико" означает, что наблюденное значение XІ имеет малую вероятность, то есть превосходит критическое значение, которое можно взять из таблиц распределения хи-квадрат. Так как вероятность Р ( ≥ XІ) - малая величина, то маловероятно случайно получить такое же, как в опыте, или еще большее расхождение между вектором частот и вектором вероятностей.

Асимптотический характер теоремы Пирсона, лежащий в основе этого правила, требует осторожности при его практическом использовании. На него можно полагаться только при больших n. Достаточно велико должно быть и n, и все произведения np_i. Проблема применимости аппроксимации  (непрерывное распределение) к статистике XІ, распределение которой дискретно, оказалась сложной. Согласно имеющемуся опыту, аппроксимация применима, если все ожидаемые частоты np_i > 10. Если число различных исходов k велико, граница для np_i может быть снижена (до 5 или даже до 3, если k порядка нескольких десятков). Чтобы соблюсти эти требования, на практике порой приходится объединять несколько исходов и переходить к схеме Бернулли с меньшим k.

Вопрос о сравнении наблюденных в опыте частот с теми, которые предписывает теория (ради проверки этой теории) возникает во многих задачах. Рассмотрим способ сопоставления наблюдаемых частот с частотами, рассчитанными по модели. Обозначим наблюдаемые частоты через Н; ожидаемые (теоретические) частоты - Т. Если модель правильно описывает действительность, числа Н и Т должны быть близки друг к другу, сумма квадратов отклонений (Н - Т) І не должна быть большой. Разумно в общую сумму отдельные слагаемые вносить с различными весами, поскольку чем больше Т, тем больше Н может от него отклоняться за счет действия случая без отступления от модели. В качестве меры близости наблюдаемых и ожидаемых частот используется величина:

, (94)

где сумма берется по всем ячейкам таблицы сопряженности, служащая мерой согласия опытных данных с теоретической моделью. Если в конкретном опыте величина XІ оказывается чрезмерно большой, считают, что ожидаемые частоты слишком сильно отличаются от наблюдаемых и отвергают нулевую гипотезу.

В качестве случайных величин в работе выступают распределения Релея и Релея-Райса, что обусловлено видом распределения случайных величин при последетекторной обработке. Огибающая смеси сигнала и шума имеет распределение Релея-Райса, а огибающая только лишь шума - Релея. Однако это не ограничивает использование смоделированного датчика, поскольку алгоритм проверки критерием Хи-квадрат универсален для различных распределений.

Рисунок 39 - Эмпирическая и теоретическая плотности распределения Релея-Райса

Рисунок 40 - Эмпирическая и теоретическая плотности распределения Релея

Рисунок 41 - Эмпирическое и теоретическое распределения Релея

Результатом тестирования является однозначное решение в пользу гипотезы о принадлежности рассматриваемой выборки теоретическому распределению, либо противоположной гипотезы.

9. Заключение

В ходе работы были исследованы четыре асимптотически оптимальных алгоритма, настроенные для обнаружения на фоне нормальной и лапласовской помех, два из которых являются ранговыми. В качестве обнаруживаемого сигнала выступает узкополосный, модулированный по амплитуде и фазе сигнал со случайной начальной фазой, что подразумевает некогерентный прием. Исследуется как до, так и последетекторный обнаружитель, основанный на данных алгоритмах.

Полученные экспериментально характеристики верного обнаружения сигнала от отношения сигнал/шум подтверждают с той или иной точностью тенденцию выигрыша оптимального для данной помехи алгоритма над неоптимальными, что подтверждено расчетами коэффициента асимптотической оптимальной эффективности. Также подтверждена идентичность характеристик АО ранговых и АО неранговых алгоритмов, настроенных на одну и ту же помеху. Показано, что характеристики алгоритмов при последетекторном приеме значительно снижаются (порядка 7 дБ), что связано с тем, что они перестают быть асимптотически эффективными.

Наибольшей устойчивостью по итогам моделирования обладает алгоритм Ван-дер-Вардена, настроенный на гауссову помеху: проигрыш составил - 1.49 дБ. Наихудшую устойчивость демонстрирует линейный алгоритм в условиях сравнения со знаковым алгоритмом - 2.03 дБ. При рассмотрении работы алгоритмов на фоне помех с показателями α=3,4 можно заключить, что ранговые алгоритмы более устойчивы к изменению помеховой обстановки. В рамках последетекторного обнаружения лучший результат демонстрирует линейный алгоритм, проиграв лишь 6,21 дБ додетекторному обнаружителю.

Полученные экспериментально данные близки к ожидаемым на основании теории значениям. Расхождение теоретических и экспериментальных данных оценено с помощью доверительных интервалов.

10. Список литературы

1.      Цикин И.А. Оптимальная обработка сигналов в радиотехнических системах. Л.: ЛПИ им.М.И. Калинина, 1986.77 с.

2.      Сидоров Ю.Е. Статистический синтез автоматизированных решающих систем при априорной неопределённости. М.: Военное издательство, 1993.232 с.

3.      Левин Б.Р. Теоретические основы статистической радиотехники: В 3-х кн. М: Сов. радио, 1976. Книга третья.288 с.

4.       Курс "Введение в статистическую радиотехнику" для студентов РФФ (6-й семестр). 2002-2003 учебный год (http://www.cde. spbstu.ru/cd_ed/consulting/its/Lectures/5. rar <http://www.cde.spbstu.ru/cd_ed/consulting/its/Lectures/5.rar>).

.        <http://www.mathworks.com/help/search/doc/en/R2011a> официальный сайт Mathworks (31.01.12)

6.      Сергиенко А.Б. Цифровая обработка сигналов. СПб: Питер, 2003

.        Шеломовский В. В Электронный учебник по дисциплине "Математическая статистика", Мурманский федеральный государственный педагогический университет

8.      Райфельд М.А. Использование устойчивых показателей зависимости наблюдений при адаптации ранговых критериев // Известия ВУЗов России, Радиоэлектроника, 2009, вып.1, с.63-67.

9.      Бирюков М.Н. Выражения математического ожидания, дисперсии и условных вероятностей знаковых и ранговых обнаружителей Неймана-Пирсона в шуме и потоке помех // Радиотехника, 2006, №6, с.101-106.

10.    Жиганов С.Н., Костров В.В. Алгоритмы обнаружения сигналов с постоянным уровнем ложных тревог // Радиотехника, 2006, №6, с.111-114.

11.    Бирюков М.Н. Синтез непараметрических обнаружителей Неймана-Пирсона в условиях совместного воздействия шума и размытого (интенсивного) потока помех // Радиотехника, 2007, №6, с.68-71.

12.    Баринов С.П. Характеристики обнаружителя радиосигнала при наличии имитирующих помех и гауссовского шума // Радиотехника, 2007, №7, с.49-51.

13.    Пильч В.А., Сидоров Ю.Е. Непараметрические решающие процедуры в системах обработки информации. Материалы Всероссийской межвузовской научно-технической конференции студентов и аспирантов. Радиофизический факультет. СПб, изд. СПбГПУ, 2008, с.22-24.

14.    Лаврентьев Н.В., Сидоров Ю.Е. Исследование помехоустойчивости обнаружителей радиосигналов. Материалы Всероссийской межвузовской научно-технической конференции студентов и аспирантов. Радиофизический факультет. СПб, изд. СПбГПУ, 2008, с.24-25.

15.    Шумилов А.В., Сидоров Ю.Е. Ранговый обнаружитель импульсных сигналов в неизвестных шумах. Материалы Всероссийской межвузовской научно-технической конференции студентов и аспирантов. Радиофизический факультет. СПб, изд. СПбГПУ, 2008, с.30-31.

16.    Остроумов И.В., Кукуш А.Г., Харченко В.П. Оценка вероятности правильного распознавания по правилу Байеса при неточно известной плотности распределения // Известия высших учебных заведений: Радиоэлектроника 2007, Киев, т.50, № 11, с.60-68.

17.    Сидоров Ю.Е., Гарбар К.А. Статистическое имитационное моделирование обнаружителя некогерентной пачки импульсов // Научно-технические ведомости СПбГПУ, 2009, № 3, С.61 - 68.

18.    Сидоров Ю.Е., Пильч В.А. Ранговый обнаружитель импульсного сигнала на фоне шумов с неизвестным распределением // Научно-технические ведомости СПбГПУ, 2009, №4. С.71 - 76.

19.    Сидоров Ю.Е., Лаврентьев Н.В. Оптимальный обнаружитель радиосигналов: решающее правило, статистическое имитационное моделирование // Труды СПбГТУ, 2008, №507. С.118 - 124.

20.    Сидоров Ю.Е., Бельченко Ю.Г. Оптимальный обнаружитель узкополосного сигнала с неизвестной несущей частотой // Научно-технические ведомости СПбГПУ, 2009, № 3. С.74 - 80.

Приложения

Приложение А

 

Моделирование знакового алгоритма (остальные по аналогии)

function P=SignStat (a, n, lambda, C, m)

% функция реализует алгоритм обнаружения сигнала S на фоне помехи N с

% используется знаковый алгоритм=100; %частота несущей=10; %частота АМ=6; %частота ФМ=2000; %частота дискретизации=1/fs; %период дискретизации= [1: n];=2*pi*rand; %равномерно распределенная на (0, 2Пи) случайная фаза=1-0.6*sin (2*pi*f2*dt*k); %амплитудная модуляция a (t)=sin (2*pi*f3*dt*k); %фазовая модуляция=at. *cos (2*pi*f1*dt*k+2*pi*ft); %синусоидальная составляющая узколосного сигнала=at. *sin (2*pi*f1*dt*k+2*pi*ft); %косинусоидальная составляющая узколосного сигнала=cos (Fi); %составляющая со случайной фазой=sin (Fi); %составляющая со случайной фазой=F1. *S1;=F2. *S2;= (s1+s2); %узкополосный сигнал=S. *S; % почленное перемножение=sum (E); %энергия сигнала=zeros (m,n); %резервирование=zeros (m,n);i=1: m=rand (1,n); %случайная величина, распред. равномерно на (0,1)j=1: ny (1,j) <0.5(i,j) =log (2*y (1,j));N (i,j) =-log (2* (1-y (1,j)));;; %шумовые отсчёты (по Лапласу);

%for i=1: m

% N (i,:) =randn (1,n); %шумовые отсчёты (по Гауссу)

%nd; %СКО=1

%for i=1: m

% N (i,:) =InverseF (4,0.01,n); %шумовые отсчёты для альфа=3,4

%end;i=1: m(i,:) =N (i,:) +lambda*S; %отсчёты входного сигнала;=sign (X); %преобразование для случая лапласовской помехи=F*S1'; %вычисление первой компоненты статистики (s1' - транспонированная)=F*S2'; %вычисление второй компоненты статистики= (Y1. ^2+Y2. ^2); %статистика (столбец m)= (1/m) *sum (Y); %мат. ожижание статистики=sqrt ( (1/m) *sum ( (Y-MeanY). ^2)); %СКО статистикиlambda==0=norminv (1-a) *SigmaY; %вычисление порога%в остальных случаях в качестве порога будет взято соответствующее

%значение из списка входных переменных(1) =MeanY;(2) =SigmaY;(3) =sum (Y>C) /m; %вероятность превышения порога(4) =C;(5) =sqrt ( (1/m) *sum ( ( (Y>C) - P (3)). ^2)); %СКО вероятности обнаружения(6) =Energy;

Моделирование последетекторного алгоритма (остальные по аналогии)

function P=LinStatAfterD (a, n, lambda, C, m)=100; %частота несущей=10; %частота АМ=6; %частота ФМ=2000; %частота дискретизации=1/fs; %период дискретизации= [1: n];=2*pi*rand; %равномерно распределенная на (0, 2Пи) случайная фаза=1-0.6*sin (2*pi*f2*dt*k); %амплитудная модуляция a (t)=sin (2*pi*f3*dt*k); %фазовая модуляция=cos (2*pi*f1*dt*k); %ВЧ синусоидальная составляющая узкополосного сигнала=sin (2*pi*f1*dt*k); %ВЧ косинусоидальная составляющая узкополосного сигнала=at. *cos (2*pi*ft+Fi); %НЧ квадратурная составляющая со случайной фазой=at. *sin (2*pi*ft+Fi); %НЧ квадратурная составляющая со случайной фазой=F1. *S1;=F2. *S2;= (s1+s2); %узкополосный сигнал с ФМ+АМ

%envelop_theor=sqrt (F1. *F1+F2. *F2);=S. *S; % почленное перемножение=sum (E); %энергия сигнала=zeros (m,n); %резервирование=zeros (m,n);=zeros (m,n);=zeros (m,n);

%for i=1: m

%y=rand (1,n); %случайная величина, распред. равномерно на (0,1)

%for j=1: n

% if y (1,j) <0.5

% N (i,j) =log (2*y (1,j));

% else N (i,j) =-log (2* (1-y (1,j)));

% end;

%end; %шумовые отсчёты (по Лапласу)

%for i=1: m

% N (i,:) =InverseF (4,0.01,n); %шумовые отсчёты для альфа=3,4

%end;i=1: m(i,:) =N (i,:) +lambda*S; %отсчёты входного сигнала;= [0.00214878098764361,-0.000508941564030241,-0.000835556005369367,-0.00137992698650711,-0.00212617978232506,-0.00305493668134725,-0.00413953304729004,-0.00534156091311405,-0.00660960942525603,-0.00787935696228989,-0.00907346613500459,-0.0101041722344159,-0.0108774805994459,-0.0112942994686013,-0.0112583337591169,-0.0106795092121329,-0.00947709806013780,-0.00759132447219574,-0.00498102178544803,-0.00163202482478250,0.00244043069481508,0.00719097339583034,0.0125428104901388,0.0183890001131049,0.0245956847756615,0.0310046913294858,0.0374393103809241,0.0437190055043905,0.0496441632736301,0.0550338926479575,0.0597136573238143,0.0635284223119868,0.0663503916867478,0.0680831680136240,0.0686673650716663,0.0680831680136240,0.0663503916867478,0.0635284223119868,0.0597136573238143,0.0550338926479575,0.0496441632736301,0.0437190055043905,0.0374393103809241,0.0310046913294858,0.0245956847756615,0.0183890001131049,0.0125428104901388,0.00719097339583034,0.00244043069481508,-0.00163202482478250,-0.00498102178544803,-0.00759132447219574,-0.00947709806013780,-0.0106795092121329,-0.0112583337591169,-0.0112942994686013,-0.0108774805994459,-0.0101041722344159,-0.00907346613500459,-0.00787935696228989,-0.00660960942525603,-0.00534156091311405,-0.00413953304729004,-0.00305493668134725,-0.00212617978232506,-0.00137992698650711,-0.000835556005369367,-0.000508941564030241,0.00214878098764361;];

%Коэффициенты фильтраi=1: m(i,:) =X (i,:). *S1;(i,:) =conv (p1 (i,:),h);(i,:) =X (i,:). *S2;(i,:) =conv (p2 (i,:),h);=sqrt (I. *I+Q. *Q);=zeros (1,n);j=1: mi=34: length (X) - 35(j, i-33) =X (j, i);;; %Процедура фильтрации и выделение огибающей=zeros (m,1);=zeros (m,n);j=1: m(j) = (1/n) *sum (envelop (j,:));(j,:) =envelop (j,:) - Meanenvelop (j);; %огибающая без постоянной составляющей=envelop2; %преобразование для случая гауссовой помехи= ( (at). * (at));=F*at2'; %статистика (столбец m)= (1/m) *sum (Y); %мат. ожижание статистики=sqrt ( (1/m) *sum ( (Y-MeanY). ^2)); %СКО статистикиlambda==0=norminv (1-a) *SigmaY; %вычисление порога%в остальных случаях в качестве порога будет взято соответствующее

%значение из списка входных переменных(1) =MeanY;(2) =SigmaY;(3) =sum (Y>C) /m; %вероятность превышения порога

%P (3) =1-normcdf (C, MeanY, SigmaY); %эквивалентная формула(4) =C;(5) =sqrt ( (1/m) *sum ( ( (Y>C) - P (3)). ^2)); %СКО вероятности обнаружения(6) =Energy;

Формирование интегральной функции распределения помехи

function D=Distribution (alpha, epsilon)

% alpha - параметр распределения помехи

% Функция выдаёт на выходе интегральную функцию распределения F (x),

% ограниченную отрезком рассмотрения [-T, T] и заданную таблично:=fzero (@ (t) 1-epsilon-gammainc (t^alpha, 1/alpha), [1, 500]); %здесь

%вычисляется граница интервала [-T; T], на котором следует рассматривать

%функции F (x) и W (x), исходя из значения параметра epsilon.dt %глобальная переменная=0.01; %dt - шаг дискретизации функции F (x)=-T: dt: T; %значения аргумента=size (t); %размерность вектора=zeros (1, s (2)); %резервированиеi=1: s (2) %формирование F (x)t (1, i) <=0(1, i) = (1/2) * (1-gammainc ( (abs (t (1, i))) ^alpha, 1/alpha));F (1, i) = (1/2) * (1+gammainc ( (abs (t (1, i))) ^alpha, 1/alpha));;;=zeros (2, s (2) +2); %таблица значений функции F (x)(1, 1) =-T-dt;(2, 1) =0;(1, 2: s (2) +1) =t;(2, 2: s (2) +1) =F;(1, s (2) +2) =t (s (2)) +dt;(2, s (2) +2) =1;

Формирование шумовой выборки

function P=InverseF (alpha, epsilon, n)

% Функция выдаёт на выходе случайную вектор-строку длиной n,

% элементы которой являются реализациями случайной величины,

% распределённой по закону F (x)=Distribution (alpha, epsilon); %ф-ция F (x)=rand (1,n); %случ. величина с равномер. распред-ем на [0; 1]=zeros (1,n); %случ. величина с распред-ем Fj=1: n %формируем случ. величину ydistrF=2;yrand (1, j) >D (2, i)=i+1;(1,j) = (D (1, i) +D (1, i-1)) /2;_Di_1=ydistrF*sqrt (gamma (1/alpha) /gamma (3/alpha));

%случайная величина ydistr_Di_1 имеет дисперсию равную 1=ydistr_Di_1;

Моделирование характеристики алгоритма

function P=Lin_DetectAfterD (m,n)=1e-3; %вероятность ложной тревоги,= [0.1: 0.05: 1]; %амплитуда сигнала=zeros (2, length (lambda)); %резервирование=0; %C - порог принятия решения=LinStatAfterD (a, n, 0, C, m); %вычисление порога для случая отсутствия сигнала

% (в данном случае порог С может быть любым, т.к. он вычисляется внутри процедуры SignStat)i=1: length (lambda)=LinStatAfterD (a, n, lambda (i), S0 (4), m);(1, i) =S (3); %записыавем вероятность правильного обнаружения(3, i) =S (1); %мат. ожижание статистики Y(4, i) =S (2); %CKO Y(5, i) =S (5); %СКО вероятности обнаружения(2,:) =20*log10 (lambda*sqrt (S (6) /2)); %значения аргумента для построения графика (1-beta) от h

%h - отношение сигнал-шум(2);(P (2,:), P (1,:)) %графическое изображение полученной зависимостиon;('Вероятность обнаружения Линейный')

Вычисление теоретического значение КАОЭ

function Ro=KAOE (alpha,beta) %вычисление коэффициента относительной

%ассимптотической эффективности алгоритма,

%настроенного на помежу с Бэта в качестве показателя экспоненты плотности

%распределения при воздействии с помехой с Альфа относительно алгоритма,

%оптимального для этой помехи.= (gamma ( (beta+alpha-1) /alpha)) * (gamma ( (beta+alpha-1) /alpha)); %числитель= (gamma ( (2*beta-1) /alpha) *gamma ( (2*alpha-1) /alpha)); %знаменатель=10*log10 (up/down);

Вычисление рангового вектора

function R=rang (n)=size (n); %размеры вектора=zeros (s (2)); %резервированиеi=1: s (2)j=1: s (2)(i,j) =0.5*sign (n (j) - n (i)) +0.5; %матрица знаков разностей;;=sum (M) +0.5; %вектор рангов

Моделирование датчика случайных величин и проверка работоспособности по критерию Хи-квадрат

function P=RayRicetest (m,N,D);=10000; %число членов выборки=1; %масштабирующий множитель для релея=10; %параметр смещения (центр плотности)=100; %число интервалов (степени свободы)= ncx2rnd (B, D, [1 m]); %выборка сл. величин, распределенных по релею-райсу(1)=max (R); %вычисление границ интервалов=min (R);=linspace (bot,top,N+1);

[n, whichBin] =histc (R,biedges); %количество попаданий в каждый интервал(1)(biedges,n,'r'); %экспериментальная плотность распределения('экспериментальная плотность распределения')oni=3: length (n) - 30 %коррекция крайних интервалов (редких частот)(i-2) =n (i);(i-2) =biedges (i);;(bbiedges,nn,'g'); %экспериментальная плотность распределенияon %с учетом коррекции= cumsum (nn) /m; %вычисление функции распределения выборки(2)(bbiedges,ce,'g')('экспериментальная функция распределения')on=min (R): (max (R) - min (R)) / (N): max (R);i=3: length (X) - 30 %коррекция крайних редких частот(i-2) =X (i);;(1)= ncx2pdf (XX, B, D); %теоретическая плотность релея-райса

%plot (f)=f*m* ( (max (R) - min (R)) /N);(XX,ff)off= cumsum (ff) /m; %вычисление теоретич. функции распределения(2)(bbiedges,ct)off= chi2inv (0.95,N-1); %уровень значимости 0,05

%Вероятность получить значение сл. вел.,

%распределенной хи^2 с V=N более L

%составляет 5%.= ( (nn-ff). ^2). /ff; %вычисление критерия=sum (xi);(1) =L;(2) =XI;P (2) >P (1)(3) =false; %единица - распределение принадлежит Р-РP (3) =true; %ноль - распределение не принадлежит Р-Р