Этногенез восточных славян
Міністерство освіти і науки
України
Національний авіаційний
університет
Кафедра
інформаційно-вимірювальних систем
Курсова робота
з дисципліни: «Спеціальні
глави математики»
Виконав: студент
Перевірив: к.т.н. Марченко Н.Б.
Варіант № 5
Київ 2009
Варіант
граф матриця
математична логіка
Номер розрахункового варіанту m визначається за списком групи: m=5.
Курсова робота повинна складатись з двох частин:
Пояснювальної записки та Додатку. В пояснювальній записці всі символи і
позначення беруться з [1] та з запропонованих завдань, не допускається вживання
програмних символів, в Додатку символіка вільна, але повинна відповідати певній
одній системі, а також обов’язково повинна бути описана відповідність символіки
кожної програми та позначень вживаних в тексті Пояснювальної записки.
Пояснювальна записка повинна містити:
текст завдань (без змін і спотворень) ;
постановку кожної задачі;
числові значення параметрів визначені за номером варіанта та
вказані в завданні по яких розв’язується задача; а також їх фізичні
розмірності;
розгорнуті розв’язки з вказівкою усіх використовуваних
основних формул, їх номерів та сторінок в літературі, з якої вони взяті;
зведення результатів;
графічні ілюстрації і висновки; графіки повинні мати
оцифровані вісі, а їх масштаби повинні бути вибрані так, щоб кожну криву можна
було відслідкувати ( не допускаються суцільні заштриховки чи зображення окремих
фрагментів, які не дають уявлення про графік, що ілюструється); якщо
зображаються на одному рисунку графіки двох кривих в спільній системі
координат, то вони повинні відрізнятись, наприклад суцільна крива, крапки,
пунктир і ін.
список використовуваної літератури,
всі основні формули та математичні вирази повинні мати
порядкові номери, сторінки пронумеровані.
Додатки включають:
обчислювальні програми, алгоритми та коментарі до них;
результати розрахунків; графічні побудови,
основні формули в програмі повинні бути пронумеровані
окремими номерами з буквою Д. Малюнки підписані і теж пронумеровані окремо.
Реферат
Об'єкт дослідження - задачі з дисципліни «Спеціальні глави
математики».
Мета роботи: узагальнення і систематизація знань з дисципліни
«Спеціальні глави математики», отриманих протягом навчального семестру.
Закріплення пройденого матеріалу, а саме з теорії множин, математичної логіки,
теорії графів та теорії рядів.
Зміст
Реферат
. Вступ
. Основні позначення
.Пояснювальна записка
Завдання 1
Завдання 2
Завдання 3
Завдання 4
Завдання 5
Список використаної літератури
Додатки
Вступ
Дана курсова робота проводиться з метою більш поглибленого
вивчення дисципліни “Спеціальні глави математики” та для набуття навиків
самостійного вирішення заданих задач.
Для успішного виконання КР студент повинен вміти працювати з
літературою, знати необхідний матеріал для виконання роботи, а саме, з теорії
множин, математичної логіки, теорії множин та графів.
Завдання №1
Розв'язання задач з теорії множин та математичної логіки
Довести і навести діаграму Ейлера-Вена

Завдання №2
Записати таблицю істинності висловлювань

Завдання №3

Для заданого графа 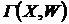 з
з
 :
:
. Знайти число ребер  та
число вершин відповідного повного графа.
та
число вершин відповідного повного графа.
. Визначити характеристики графа 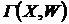 у
відповідності до таблиці 1
у
відповідності до таблиці 1
Таблиця 1
|
Характеристика графа
|
Граф 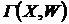
|
|
Повнота
|
|
|
Зв'язність
|
|
|
Число циклів
|
|
|
Ейлеровість
|
|
|
Гамільтоновість
|
|
3. Визначити характеристики вершини графа (заповнити
таблицю 2)
Таблиця 2
|
№вершини
|
1
|
2
|
3
|
4
|
5
|
|
Степінь вершини
|
|
|
|
|
|
|
|
Ізольована
|
|
|
|
|
|
|
|
Кінцева
|
|
|
|
|
|
|
|
Точка з'єднання
|
|
|
|
|
|
|
4. Побудувати матрицю інцидентності графа
5. Намалювати зв'язні підграфи графа 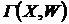 з 4 і 5 вершинами.
з 4 і 5 вершинами.
. Виписати їх матриці інцидентності.
. Мінімальним числом операцій вилучення та доповнення ребер
зробити заданий граф Ейлеровим.
. Мінімальним числом операцій вилучення та доповнення ребер
зробити заданий граф Гамільтоновим.
Завдання №4
“Розклад функцій дискретного аргументу в ряди по базисним
функціям”
Розкласти в ряд функцію 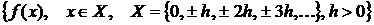 по
узагальненим степеням, побудувати графік сум перших трьох членів цього розкладу
та графік
по
узагальненим степеням, побудувати графік сум перших трьох членів цього розкладу
та графік  на одному малюнку. Зробити висновок що до характеру
наближення цього розкладу до функції
на одному малюнку. Зробити висновок що до характеру
наближення цього розкладу до функції  на
ришітці.
на
ришітці.
Функція  визначається з таблиці 3, де
визначається з таблиці 3, де  номер варіанта.
номер варіанта.
Таблиця 3
 вибирається
рівним нулеві, якщо в цій точці існує значення заданої в завданні функції, або
найближче значення з урахуванням кроку
вибирається
рівним нулеві, якщо в цій точці існує значення заданої в завданні функції, або
найближче значення з урахуванням кроку 
Завдання №5
Для процесора, що реалізує алгоритм дискретного (або швидкого)
перетворення Фур’є, при заданих значеннях обсягу вибірки  відліків вхідного сигналу і частоті дискретизації
відліків вхідного сигналу і частоті дискретизації  , вирахувати та побудувати нормовану
амплітудно-частотну характеристику
, вирахувати та побудувати нормовану
амплітудно-частотну характеристику  -го
вихідного сигналу.
-го
вихідного сигналу.
 -
номер варіанту
-
номер варіанту
Методичні
вказівки
Необхідно мати на увазі, що при частоті вхідного сигналу  , співпадаючої з частотою настройки 1-го каналу
процесора, у випадку, якщо
, співпадаючої з частотою настройки 1-го каналу
процесора, у випадку, якщо 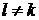 ,
відгук
,
відгук  -го каналу рівний нулю. Розрахунок значення АЧХ
достатньо проводить в трьох точках по вісі частот у кожному з інтервалів між
резонансними частотами процесора. Зручно у якості цих точок вибрати середину
інтервалу розносу резонансних частот процесора та середні точки половинок
інтервалів що утворилися.
-го каналу рівний нулю. Розрахунок значення АЧХ
достатньо проводить в трьох точках по вісі частот у кожному з інтервалів між
резонансними частотами процесора. Зручно у якості цих точок вибрати середину
інтервалу розносу резонансних частот процесора та середні точки половинок
інтервалів що утворилися.
Як і при виконанні першого завдання у пояснювальній записці треба
привести стислі теоретичні відомості та основні розрахункові відомості та
основні розрахункові співвідношення. Розрахунки проводити для вхідного сигналу
типу дискретизованої комплексної експоненти.
Таблиця 4
.Основні позначення
|
А, В, С,…, Z
|
Загальне позначення
множин, висловлень алгебри логіки
|
|
a, b, c,…,z
|
Загальне позначення
елементів множин
|
|
N(A)
|
Кількість елементів
скінченной множини А
|
|
 Узагальнений степінь Узагальнений степінь
|
|
|
 Граф (Х-множина вершин,W -множина ребер) Граф (Х-множина вершин,W -множина ребер)
|
|
|
 Різницевий оператор Різницевий оператор
|
|
|
 Різницевий оператор n-ного порядку Різницевий оператор n-ного порядку
|
|
Завдання №1
Розв'язання задач з теорії множин та математичної логіки
Довести і навести діаграму Ейлера-Вена
Згідно варіанту:

Короткі теоретичні відомості
Поняття множини - одне з основних понять математики, яке не
визначається. Множину можна уявити як сукупність деяких об’єктів, об’єднаних за
якою-небудь ознакою. При цьому передбачається, що об’єкти даної сукупності
відрізняються один від одного і від предметів, що не входять до цієї
сукупності. Множини позначаються великими літерами A, B, C, D та т. д.
Існує два основних способи завдання (опису) множин.
1) Множина А визначається безпосередньо перелічуванням
своїх елементів а1, а2, …аn, тобто записується у вигляді

) Множина А визначається як сукупність тих і тільки тих
елементів з деякої основної множини В, що мають властивість α(x). У цьому випадку використовуються
позначення  або
або  .
Таким чином, множина вважається заданою, якщо відома властивість, яку мають
елементи цієї множини.
.
Таким чином, множина вважається заданою, якщо відома властивість, яку мають
елементи цієї множини.
Операції над множинами.
Перетином (або додатком) множин А і В (позначення  або А∙В) називається множина, що складається з
елементів, які належать одночасно як множин А, так і множині В:
або А∙В) називається множина, що складається з
елементів, які належать одночасно як множин А, так і множині В:
 (1)
(1)
На рис. 1.а множина  заштрихована.
заштрихована.
Розглянемо властивості операції перетину:
) 
) 
) 
) 
) 
) 
Об’єднанням (або сумою) множин А і В (позначення  або А+В) називається множина, що складається з усіх
елементів, які належать хоча б одній з цих множин.
або А+В) називається множина, що складається з усіх
елементів, які належать хоча б одній з цих множин.
 (3)
(3)
На рис. 1.б множина  заштрихована.
заштрихована.
Розглянемо властивості операції об’єднання:
) 

) 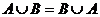
) 
) 
) 
Різницею множин (позначення А\В) називається множина, що
складається з елементів, як належать множині А, але не належать множині В. На
рис. 1.в множина А\В заштрихована.
 (4)
(4)
Розглянемо властивості операції різниці:
1) 
) 
) 
) 
) 
Доповненням множини А (позначення  )
називається множина елементів універсальної множини Ω, не приналежних множині А.
)
називається множина елементів універсальної множини Ω, не приналежних множині А.

Якщо Ω
зобразити у вигляд прямокутника,
то множина  заштрихована на рис. 1.г.
заштрихована на рис. 1.г.
Розглянемо основні властивості операції доповнення:
) 
) 
) 
) 
) 

Доведення: Нехай  спираючись на властивість різниці можна
стверджувати,що
спираючись на властивість різниці можна
стверджувати,що 

Тепер нехай  спираючись на властивості операцій пертину
спираючись на властивості операцій пертину
Та різниці,ми отримаємо  ,а
отже
,а
отже 
Отже ми можемо сказати,що А є пдмножино С, а враховуючи оперцію
різниці, В виключається.
Нехай  , тоді не існує таких
, тоді не існує таких  і
і
 , тобто множина А буде підмножиною В.
, тобто множина А буде підмножиною В.
Отже наша умова  виконується
виконується
Наведемо діаграми Ейлера-Вена









Отже твердження  - вірне, що і було доведено
- вірне, що і було доведено
Висновок: в результаті нескладних методів розв'язання задач з теорії
множин та математичної логіки та за допомогою діаграм Ейлера-Вена було доведено
вираз  . Результат отримали однаковий.
. Результат отримали однаковий.
Завдання №2
Записати таблицю істинності висловлювань

Складні висловлення утворюються з простих за допомогою
логічних операцій. Розглянемо основні з них.
Означення. Запереченням (інверсією) висловлення  називається таке складне висловлення
називається таке складне висловлення 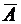 , яке хибне, якщо
, яке хибне, якщо  -
істинне, і істинне, якщо
-
істинне, і істинне, якщо  - хибне.
- хибне.
Наведене в означенні можна записати з допомогою таблиці істинності.
|
 
|
|
|
0
|
1
|
|
1
|
0
|
Означення. Еквівалентністю двох висловлень  називається таке складне висловлення
називається таке складне висловлення  , яке істинне тоді і тільки тоді, коли значення
істинності висловлень
, яке істинне тоді і тільки тоді, коли значення
істинності висловлень  однакові, і хибне - якщо різні.
однакові, і хибне - якщо різні.
Таблиця істинності еквівалентності:
Означення. Імплікацією двох висловлень  називається
таке складне висловлення
називається
таке складне висловлення  (інше позначення
(інше позначення  ),
яке хибне тоді і тільки тоді, коли
),
яке хибне тоді і тільки тоді, коли  ,
а
,
а  .
.
Таблиця істинності для імплікації така:
Розв’язання:

Для зручності будемо робити розрахунки в таблиці.
Отримали таку таблицю істиності:
Таблиця 5
|
А
|
В
|
 
|
|
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
1
|
|
1
|
0
|
0
|
0
|
|
1
|
1
|
1
|
1
|
Висновок: за допомогою простих логічних операцій отримали таблицю
істиності виразу 
Завдання №3
Граф - множина точок, що сполучені деякими відрізками.
Неорієнтовані (ненапрямлені) графи
Означення. Нехай множина  -
множина точок,
-
множина точок,  - множина усіх двоелементних невпорядкованих
підмножин множини X (множина відрізків, які сполучають точки з X). Графом
(неорієнтованим, ненапрямленим) називають систему
- множина усіх двоелементних невпорядкованих
підмножин множини X (множина відрізків, які сполучають точки з X). Графом
(неорієнтованим, ненапрямленим) називають систему  множин X і W, де
множин X і W, де  (X
- множина точок - вершин, W - множина відрізків - ребер).
(X
- множина точок - вершин, W - множина відрізків - ребер).
Якщо  і
і  ,
то
,
то  називається скінченним графом, в іншому випадку
називається скінченним графом, в іншому випадку  - нескінченний граф.
- нескінченний граф.
Означення.  - повний граф
- повний граф  якщо
якщо
 .
.
Означення.  - порожній граф
- порожній граф  якщо
якщо
 .
.
Означення. Нехай  - граф. Матриця
- граф. Матриця  ,
складена з чисел
,
складена з чисел 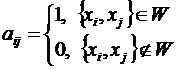 , називається матрицею інцидентності (суміжності) графа
, називається матрицею інцидентності (суміжності) графа
 .
.
Іншими словами,  , коли вершини
, коли вершини  та
та
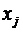 не з'єднані ребром і
не з'єднані ребром і 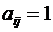 ,
коли ці вершини з'єднані ребром.
,
коли ці вершини з'єднані ребром.
Степінь вершини графа
Означення. Нехай  - граф,
- граф,  ,
,  - вершини цього графа. Вершини
- вершини цього графа. Вершини  та
та 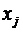 інцидентні
інцидентні

 (вершини
(вершини  та
та
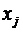 сполучені ребром).
сполучені ребром).
Означення. Нехай  - граф,
- граф,  .
. 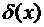 - степінь (валентність) вершини x
- степінь (валентність) вершини x  число вершин, інцидентних з x (число ребер, що
виходять з вершини x).
число вершин, інцидентних з x (число ребер, що
виходять з вершини x).
Теорема Ейлера.  (кожне ребро при підрахунку суми степенів усіх вершин
враховується два рази).
(кожне ребро при підрахунку суми степенів усіх вершин
враховується два рази).
Означення.  . Якщо
. Якщо  ,
то вершина
,
то вершина  називається кінцевою. Якщо
називається кінцевою. Якщо  , то вершина
, то вершина  називається
ізольованою.
називається
ізольованою.
Підграфи
Означення. Нехай  - граф. Впорядкований набір елементів (ребер) з
- граф. Впорядкований набір елементів (ребер) з  :
:  називається
маршрутом. Якщо
називається
маршрутом. Якщо  , то маршрут називається замкненим, інакше -
відкритим.
, то маршрут називається замкненим, інакше -
відкритим.
Означення. Маршрут, у якого всі ребра різні називається ланцюгом, що
сполучає (з'єднує) вершини  і
і
 (кінці ланцюга).
(кінці ланцюга).
Означення. Ланцюг, у якого  називається
простим ланцюгом (див. рис. 2.).
називається
простим ланцюгом (див. рис. 2.).

Рис.2.
Означення. Ланцюг називається замкненим (або циклом), якщо  .
.
Означення. Граф 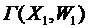 називається підграфом графа
називається підграфом графа  , якщо
, якщо  .
.
Означення. Граф називається зв’язним, якщо будь-які дві його
вершини можна сполучити простим ланцюгом.
Незв'язний граф складається з k>1 окремих підграфів,
кожний з яких є зв’язним графом.
Означення. Граф без циклів називається ациклічним або лісом.
Означення. Зв’язний граф без циклів називається деревом.
Теорема 1. Нехай  - зв'язний граф.
- зв'язний граф.
 1.
- дерево тоді і тільки тоді, коли
1.
- дерево тоді і тільки тоді, коли 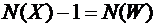 .
.
 2.
містить хоча б один цикл тоді і тільки тоді, коли
2.
містить хоча б один цикл тоді і тільки тоді, коли  .
.
Зауваження. По суті, 2-й пункт теореми 1 є наслідком першого
і навпаки. Але нам тут зручніше розглядати їх разом.
Наслідок. При заданому 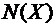 ,
дерево - це зв'язний граф, який має найменшу кількість ребер.
,
дерево - це зв'язний граф, який має найменшу кількість ребер.
Ейлерові графи
Означення. Зв’язний граф  називається
ейлеровим, якщо існує цикл, який проходить через кожне його ребро тільки один
раз.
називається
ейлеровим, якщо існує цикл, який проходить через кожне його ребро тільки один
раз.
Означення. Зв'язний граф  називається
напівейлеровим,
називається
напівейлеровим,
якщо існує ланцюг, який проходить через кожне його ребро тільки один
раз.
Теорема. Зв’язний граф  ейлеровий
тоді і тільки тоді, коли степінь кожної його вершини - парне число.
ейлеровий
тоді і тільки тоді, коли степінь кожної його вершини - парне число.
Наслідок. Зв’язний граф  напівейлеровий,
якщо існує не більше двох його вершин непарного степеня.
напівейлеровий,
якщо існує не більше двох його вершин непарного степеня.
Означення. Зв'язний граф  називається
гамільтоновим, якщо існує цикл, який проходить через кожну його вершину тільки
один раз.
називається
гамільтоновим, якщо існує цикл, який проходить через кожну його вершину тільки
один раз.
Означення. Зв'язний граф  називається
напівгамільтоновим, якщо існує ланцюг, який проходить через кожну його вершину
тільки один раз.
називається
напівгамільтоновим, якщо існує ланцюг, який проходить через кожну його вершину
тільки один раз.

Рис.3. Граф 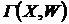
Розв’язування:
Для заданого графа 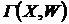 з
з
 :
:
. Знайдемо число ребер  та
число вершин відповідного повного графа.
та
число вершин відповідного повного графа.


. Визначимо характеристики графа 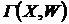 у
відповідності до таблиці 6
у
відповідності до таблиці 6
Таблиця 6
|
Характеристика
графа
|
Граф 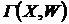
|
|
Повнота
|
Неповний
|
|
Зв'язність
|
Незв’зний
|
|
Число циклів
|
3 цикл {4-1-2-3}{4-5-2-3}{4-5-3}
|
|
Ейлеровість
|
Не Ейлерів
|
|
Гамільтоновість
|
Не Гамільтоновий
|
3.
Визначимо характеристики вершини графа
Таблиця 7
|
№вершини
|
1
|
2
|
3
|
4
|
5
|
6
|
|
Степінь вершини
|
2
|
3
|
3
|
3
|
3
|
0
|
|
Ізольована
|
-
|
-
|
-
|
-
|
-
|
+
|
|
Кінцева
|
-
|
-
|
-
|
-
|
-
|
-
|
Точка з'єднання.......................... -......................... -......................... -......................... -......................... -......................... -........................... 
4. Побудувати матрицю інцидентності графа
Згідно з визначенням будуємо матрицю інцидентності графа:



. Намалювати зв'язні підграфи графа 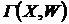 з 4 і 5 вершинами. Виписати їх матриці інцидентності.
з 4 і 5 вершинами. Виписати їх матриці інцидентності.
. Мінімальним числом операцій вилучення та доповнення ребер
зробити заданий граф Ейлеовим.

7. Мінімальним числом операцій вилучення та доповнення ребер
зробити заданий граф Гамільтоновим.

Завдання №4
Розглянемо простір функцій дискретного аргументу (тобто, таких функцій,
областю визначення яких є впорядкована дискретна множина):  .
.
Різницевий оператор у просторі функцій  вводиться
наступним чином:
вводиться
наступним чином:
 ,
,  (5)
(5)
Крім різницевого оператора вводять ще оператор попередньої різниці:  , (при
, (при  :
:  ), який зв’язаний з різницевим оператором формальним
співвідношенням:
), який зв’язаний з різницевим оператором формальним
співвідношенням:  при
при  (
( ).
).
Властивості різницевого оператора:
 1. ,
1. , , тобто різницевий оператор є лінійним.
, тобто різницевий оператор є лінійним.
 2. .
2. .
 3.
при
3.
при  .
.
При  маємо:
маємо:  ,
де
,
де  (
( -
оператор зсуву).
-
оператор зсуву).
 4. .
4. .
 - різницевий оператор
- різницевий оператор  -ного порядку (повторне (
-ного порядку (повторне ( разів) застосування різницевого оператора
разів) застосування різницевого оператора  ).
).
Теорема. Для різницевого оператора n-го порядку справедливим є
наступне співвідношення:

Узагальнений степінь
Функцію

називають узагальненим степенем. Якщо  ,
то замість
,
то замість  вживається позначення
вживається позначення
 .
.
Для натуральних  маємо:
маємо:
 при
при
 ,
,
зокрема, 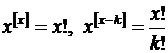 . Кількість розміщень з
. Кількість розміщень з  по
по


Розклади функцій за узагальненими степенями
Аналогічно розкладу функцій неперервного аргументу в ряди за
степеневими функціями  (ряди Тейлора), можна будувати розклад деякої функції
(ряди Тейлора), можна будувати розклад деякої функції
 в ряд за узагальненими степенями
в ряд за узагальненими степенями  :
:


Розв’язання
Згідно з варіантом m=5,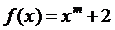 ,
,

Проведемо розрахунок різницевого оператора згідно формули (6)
отримаємо:

Знайдемо коефіцієнти  в
точці
в
точці  скориставшись формулою:
скориставшись формулою:

Отримаємо:




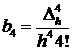
Згідно формули (7) отримаємо:

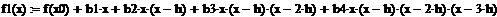
По отриманим значенням побудуємо графік:

Рис.4. Графік функції та цієї ж функції розкладеної за узагальненими
степенями
Додатки:
Завдання №5
Для процесора, що реалізує алгоритм дискретного (або швидкого)
перетворення Фур’є, при заданих значеннях обсягу вибірки  відліків вхідного сигналу і частоті дискретизації
відліків вхідного сигналу і частоті дискретизації  , вирахувати та побудувати нормовану
амплітудно-частотну характеристику
, вирахувати та побудувати нормовану
амплітудно-частотну характеристику  -го
вихідного сигналу.
-го
вихідного сигналу.
 -
номер варіанту
-
номер варіанту
Таблиця
Короткі теоретичні відомості.
В загальному випадку, рівняння  має
має
 незвідних коренів
незвідних коренів 
Нехай:  .
.
Побудуємо матрицю  .
.
Отримаємо:

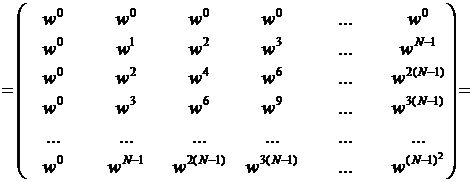

Для  справедлива властивість:
справедлива властивість:  , де
, де  -
остача від ділення
-
остача від ділення 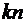 на
на  ,
,  . Дійсно, можемо записати
. Дійсно, можемо записати  , де
, де  -
неповна частка від ділення
-
неповна частка від ділення 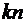 на
на
 . Тому
. Тому  .
.
Матриця  симетрична:
симетрична:  .
Зокрема, другий рядок (другий стовпець) матриці
.
Зокрема, другий рядок (другий стовпець) матриці  містить
усі незвідні корені рівняння
містить
усі незвідні корені рівняння  .
.
Має місце:  , тому
, тому  -
унітарна матриця, тобто
-
унітарна матриця, тобто  .
.
Таким чином, якщо  - вектор-стовпець (в загальному випадку, з
комплексними елементами), то
- вектор-стовпець (в загальному випадку, з
комплексними елементами), то
 ,
,
де
Ортогональні перетворення  та
та
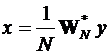 називаються парою дискретних (скінченних) перетворень
Фур’є (ДПФ).
називаються парою дискретних (скінченних) перетворень
Фур’є (ДПФ).
У розгорнутому вигляді розглянуті вище матричні перетворення можна
записати так:

 .
.
Останній вираз можна записати так:
 ,
,  , (9)
, (9)
де
 ,
,  .
.
Алгоритм швидкого перетворення Фур’є (ШПФ)
Цей алгоритм застосовується для обчислення дискретного
перетворення Фур’є і не є яким-небудь різновидом самого ДПФ.
Розглядуваний алгоритм ШПФ використовується лише при  , де
, де  -
натуральне число (відомі й інші алгоритми ШПФ, у яких
-
натуральне число (відомі й інші алгоритми ШПФ, у яких  не обов’язково має бути степенем двійки).
не обов’язково має бути степенем двійки).
Розіб’ємо масив  на дві частини:
на дві частини:
 ,
,
 .
.
Представимо тепер  -ий коефіцієнт ДПФ у вигляді:
-ий коефіцієнт ДПФ у вигляді:

 .
.
Безпосередньо видно, що перша половина коефіцієнтів ДПФ  виражається через коефіцієнти ДПФ послідовностей
виражається через коефіцієнти ДПФ послідовностей  та
та 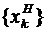 ,
тобто
,
тобто

Оскільки  , то
, то
 ,
,  .
.
Крім того, множник  ,
при
,
при  можна записати так:
можна записати так:
 .
.
Тому для другої половини множини коефіцієнтів ДПФ маємо:
 .
.
Процес повторюється по ітерації, поки не залишиться один елемент. Його
ДПФ буде він сам. Число операцій при використанні ШПФ  .
.
Розв’язання:
Вирахуємо вираз для нормованої амплітудно-частотної характеристики  -го вихідного сигналу:
-го вихідного сигналу:

Після підстановки у вираз наших даних отримуємо графік:

Рис. 5. Амплітудно-частотна характеристика  -го вихідного сигналу.
-го вихідного сигналу.
Висновок: Значення отриманої функції у точках, кратних 9 рівна
нулю, бо  і головний пелюсток зсунутий праворуч на дев’ять
позицій від нульової координати через те, що k=9.
і головний пелюсток зсунутий праворуч на дев’ять
позицій від нульової координати через те, що k=9.
СПИСОК ВИКОРИСТАННОЇ ЛІТЕРАТУРИ:
1. Марченко Б.Г., Марченко Н.Б., Фриз М.Є. Спеціальні
глави математики. Навч. посібник. - Тернопіль: Вид-во ТДТУ ім. І.Пулюя, 2004. -
159 с.
2. Марченко Б.Г., Фриз М.Є. Основи дискретної
математики. Конспект лекцій. - Тернопіль: Вид-во ТДТУ ім. І. Пулюя, 2000. - 96
с.
Додатки
Додаток 1



Додаток
2
